/Szkoła średnia/Zadania maturalne
Poprawkowy Egzamin Maturalny
z Matematyki poziom podstawowy 23 sierpnia 2011 Czas pracy: 170 minut
Zadania zamknięte
Rozwiązaniem równania 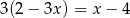 jest:
jest:
A) 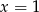 B)
B) 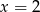 C)
C) 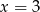 D)
D) 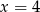
Suma liczby  i
i 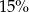 tej liczby jest równa 230. Równaniem opisującym tę zależność jest
tej liczby jest równa 230. Równaniem opisującym tę zależność jest
A) 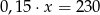 B)
B) 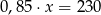 C)
C) 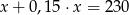 D)
D) 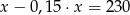
Rozwiązaniem układu równań 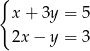 jest
jest
A) 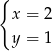 B)
B) 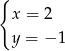 C)
C) 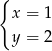 D)
D) 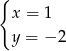
Funkcja 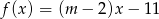 jest rosnąca, gdy
jest rosnąca, gdy
A) 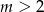 B)
B) 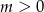 C)
C) 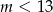 D)
D) 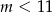
Do wykresu funkcji liniowej 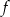 należą punkty
należą punkty 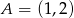 i
i 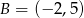 . Funkcja
. Funkcja 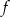 ma wzór
ma wzór
A) 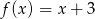 B)
B) 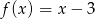 C)
C) 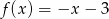 D)
D) 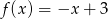
Punkt 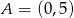 leży na prostej
leży na prostej 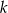 prostopadłej do prostej o równaniu
prostopadłej do prostej o równaniu 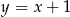 . Prosta
. Prosta 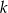 ma równanie
ma równanie
A) 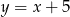 B)
B) 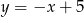 C)
C) 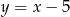 D)
D) 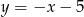
Dla pewnych liczb  i
i 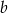 zachodzą równości:
zachodzą równości: 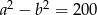 i
i 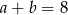 . Dla tych liczb
. Dla tych liczb  i
i 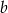 wartość wyrażenia
wartość wyrażenia 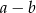 jest równa
jest równa
A) 25 B) 16 C) 10 D) 2
Liczba 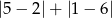 jest równa
jest równa
A) 8 B) 2 C) 3 D) -2
Liczba 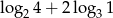 jest równa
jest równa
A) 0 B) 1 C) 2 D) 4
Zbiorem wartości funkcji kwadratowej 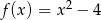 jest
jest
A) 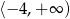 B)
B) 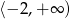 C)
C) 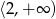 D)
D) 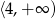
Dane są wielomiany 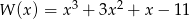 i
i 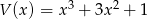 . Stopień wielomianu
. Stopień wielomianu 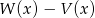 jest równy
jest równy
A) 0 B) 1 C) 2 D) 3
W ciągu geometrycznym 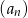 mamy
mamy 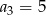 i
i 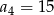 . Wtedy wyraz
. Wtedy wyraz 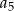 jest równy
jest równy
A) 10 B) 20 C) 75 D) 45
Ile jest liczb naturalnych czterocyfrowych o sumie cyfr równej 2?
A) 1 B) 2 C) 3 D) 4
Dane są punkty 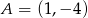 oraz
oraz 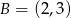 . Odcinek
. Odcinek 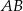 ma długość
ma długość
A) 1 B) 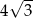 C)
C) 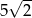 D) 7
D) 7
Kąt  jest ostry oraz
jest ostry oraz 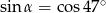 . Wtedy miara kąta
. Wtedy miara kąta  jest równa:
jest równa:
A) 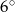 B)
B) 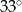 C)
C) 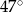 D)
D) 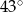
Ile wyrazów ujemnych ma ciąg 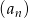 określony wzorem
określony wzorem 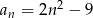 dla
dla 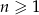 ?
?
A) 0 B) 1 C) 2 D) 3
Krawędź sześcianu ma długość 9. Długość przekątnej tego sześcianu jest równa:
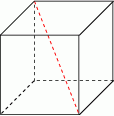
A) 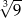 B)
B) 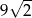 C)
C) 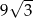 D)
D) 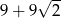
Średnia arytmetyczna sześciu liczb: 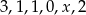 jest równa 2. Wtedy liczba
jest równa 2. Wtedy liczba  jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 30 jest równe
A) 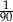 B)
B) 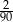 C)
C) 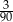 D)
D) 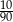
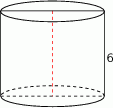
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
A) 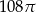 B)
B) 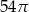 C)
C) 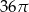 D)
D) 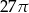
Dany jest romb o boku długości 4 i kącie ostrym 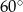 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 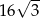 B) 16 C)
B) 16 C) 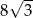 D) 8
D) 8
Kula ma objętość 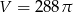 . Promień
. Promień  tej kuli jest równy
tej kuli jest równy
A) 6 B) 8 C) 9 D) 12
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Suma długości wszystkich krawędzi jest równa 90. Wtedy pole powierzchni całkowitej tego graniastosłupa jest równe
A) 300 B) 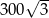 C)
C) 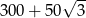 D)
D) 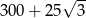
Zadania otwarte
Rozwiąż nierówność 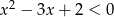 .
.
Udowodnij, że iloczyn kolejnych liczb naturalnych od 1 do 16, czyli 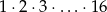 , jest podzielny przez
, jest podzielny przez 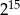 .
.
Kąt  jest ostry i
jest ostry i 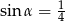 . Oblicz
. Oblicz 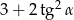 .
.
Liczby 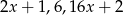 są w podanej kolejności pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Oblicz
są w podanej kolejności pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Oblicz  .
.
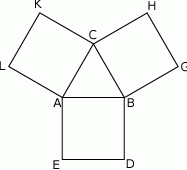
Na bokach trójkąta równobocznego 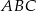 (na zewnątrz tego trójkąta) zbudowano kwadraty
(na zewnątrz tego trójkąta) zbudowano kwadraty 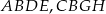 i
i 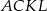 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt  jest równoboczny.
jest równoboczny.
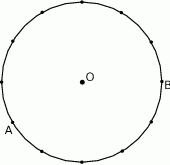
Punkty  i
i  leżą na okręgu o środku
leżą na okręgu o środku  i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 7:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.
i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 7:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.
Dane są dwa pudełka: czerwone i niebieskie. W każdym z tych pudełek znajduje się 10 kul ponumerowanych liczbami od 1 do 10. Z każdego pudełka losujemy jedną kulę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że numer kuli wylosowanej z czerwonego pudełka jest mniejszy od numeru kuli wylosowanej z niebieskiego pudełka.
Dwie szkoły mają prostokątne boiska. Przekątna każdego boiska jest równa 65 m. Boisko w drugiej szkole ma długość o 4 m większą niż boisko w pierwszej szkole, ale szerokość o 8 m mniejszą. Oblicz długość i szerokość każdego z tych boisk.
Ile jest liczb pięciocyfrowych, spełniających jednocześnie następujące cztery warunki:
(1) cyfry setek, dziesiątek i jedności są parzyste,
(2) cyfra setek jest większa od cyfry dziesiątek,
(3) cyfra dziesiątek jest większa od cyfry jedności,
(4) w zapisie tej liczby nie występuje cyfra 9.
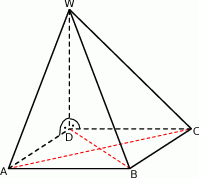
Podstawą ostrosłupa  jest prostokąt
jest prostokąt  . Krawędź boczna
. Krawędź boczna 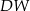 jest wysokością tego ostrosłupa. Krawędzie boczne
jest wysokością tego ostrosłupa. Krawędzie boczne 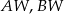 i
i 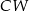 mają następujące długości:
mają następujące długości: 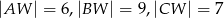 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.