/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony
(technikum) 28 lutego 2015 Czas pracy: 180 minut

Zadanie 1
(4 pkt)

Rozwiąż nierówność 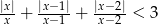|x| |x− 1| |x−2| -x-+ x−-1-+ -x−2-< 3 .

Zadanie 2
(5 pkt)

W trójkącie o obwodzie 14 jeden z boków jest dwa razy dłuższy od drugiego boku. Oblicz cosinus najmniejszego kąta, tego spośród trójkątów spełniających podany warunek, w którym suma kwadratów długości boków jest najmniejsza.

Zadanie 3
(3 pkt)

Która liczba jest większa 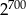2700 , czy 5300 ?

Zadanie 4
(4 pkt)

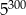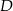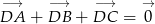Udowodnij, że jeżeli punkt D jest środkiem ciężkości trójkąta, to − → −→ −→ → DA + DB + DC = 0 .

Zadanie 5
(4 pkt)

Wyznacz zbiór wartości funkcji: 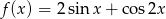f (x) = 2 sin x + cos 2x , gdzie x ∈ R .

Zadanie 6
(5 pkt)

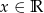Wyznacz wszystkie wartości parametrów 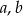a,b , dla których nierówność

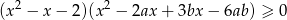
(x 2 − x − 2)(x 2 − 2ax + 3bx − 6ab) ≥ 0

jest spełniona przez każdą liczbę rzeczywistą.

Zadanie 7
(4 pkt)

Rozwiąż układ równań 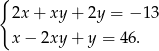{ 2x+ xy + 2y = −1 3 x− 2xy + y = 4 6.

Zadanie 8
(4 pkt)

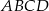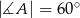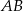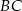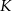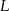Kąt ostry rombu ABCD ma miarę ∘ |∡A | = 60 . Na bokach AB i BC wybrano punkty K i L w ten sposób, że 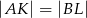|AK | = |BL | . Uzasadnij, że trójkąt 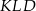KLD jest trójkątem równobocznym.

Zadanie 9
(5 pkt)

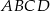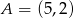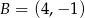Pole równoległoboku ABCD o danych wierzchołkach A = (5,2) i B = (4,− 1) jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej 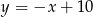y = −x + 10 , który ma obie współrzędne będące liczbami całkowitymi.

Zadanie 10
(3 pkt)

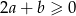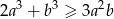Uzasadnij, że jeżeli 2a + b ≥ 0 , to 3 3 2 2a + b ≥ 3a b .

Zadanie 11
(4 pkt)

Suma krawędzi graniastosłupa prawidłowego trójkątnego jest równa 3. Dla jakiej długości krawędzi podstawy pole powierzchni całkowitej tego graniastosłupa będzie największe?

Zadanie 12
(5 pkt)

Ile jest liczb naturalnych czterocyfrowych, w których żadne dwie spośród cyfr: 1,3,5,7,9 nie sąsiadują ze sobą?

Arkusz Wersja PDF
Rozwiązania