/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom rozszerzony 23 maja 2018 Czas pracy: 180 minut
Zadania zamknięte
Jeżeli 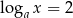 i
i 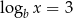 , to liczba
, to liczba 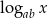 jest równa
jest równa
A) 6 B)  C)
C) 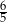 D)
D) 
Liczba 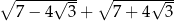 jest równa
jest równa
A) 16 B) 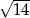 C) 4 D)
C) 4 D) 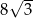
Granica ciągu 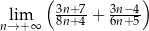 jest równa
jest równa
A) 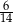 B)
B)  C)
C) 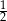 D)
D) 
Jeżeli 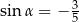 i
i 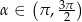 , to
, to
A) 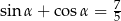 B)
B) 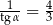 C)
C) 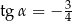 D)
D) 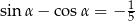
Ile rozwiązań ma równanie 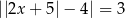 ?
?
A) 0 B) 1 C) 2 D) 4
Zadania otwarte
Wiedząc, że 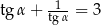 , oblicz
, oblicz 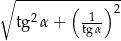 .
.
Wykaż, że dla dowolnych dodatnich liczb 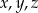 spełniona jest nierówność
spełniona jest nierówność
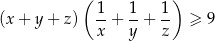
Wykaż, że jeżeli każda przekątna czworokąta wypukłego dzieli go na trójkąty o równych polach to czworokąt ten jest równoległobokiem.
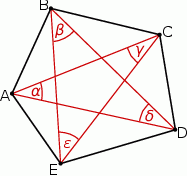
Oblicz sumę miar kątów utworzonych przez przekątne pięciokąta wypukłego.
Dla jakiej wartości parametru 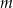 funkcje
funkcje 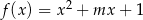 i
i 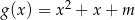 mają wspólne miejsce zerowe?
mają wspólne miejsce zerowe?
Wykaż, że równanie 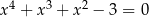 ma tylko jedno rozwiązanie które jest liczbą wymierną.
ma tylko jedno rozwiązanie które jest liczbą wymierną.
Wyznacz wszystkie pary 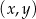 , gdzie
, gdzie  i
i 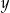 są liczbami całkowitymi spełniającymi równanie
są liczbami całkowitymi spełniającymi równanie
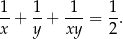
Wyznacz wszystkie wartości parametru 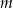 , dla których równanie
, dla których równanie 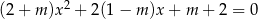 ma dwa różne pierwiastki rzeczywiste i kwadrat sumy odwrotności tych pierwiastków nie jest mniejszy od 0,5.
ma dwa różne pierwiastki rzeczywiste i kwadrat sumy odwrotności tych pierwiastków nie jest mniejszy od 0,5.
Cztery liczby tworzą ciąg geometryczny. Jeżeli od pierwszej z nich odejmiemy 2, od drugiej 3, od trzeciej 9, a od czwartej 25, to otrzymane różnice utworzą ciąg arytmetyczny. Znajdź te liczby.
W trójkącie 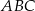 boki
boki 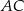 i
i 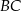 są równe. Okrąg, którego średnicą jest wysokość
są równe. Okrąg, którego średnicą jest wysokość 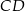 trójkąta przecina boki trójkąta w punktach dzielących te boki w stosunku 5:3 licząc od wierzchołka
trójkąta przecina boki trójkąta w punktach dzielących te boki w stosunku 5:3 licząc od wierzchołka 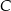 . Oblicz pole trójkąta
. Oblicz pole trójkąta 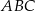 , jeżeli
, jeżeli 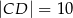 .
.
Dana jest funkcja
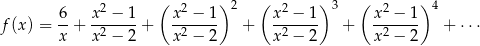
Wyznacz dziedzinę i miejsca zerowe funkcji 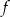 .
.

