/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 24 kwietnia 2021 Czas pracy: 170 minut
Zadania zamknięte
Liczba 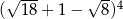 jest równa
jest równa
A) 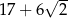 B)
B) 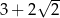 C)
C) 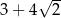 D)
D) 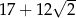
Wyrażenie 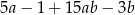 jest równe iloczynowi
jest równe iloczynowi
A) 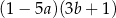 B)
B) 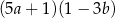 C)
C) 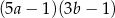 D)
D) 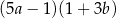
Liczba 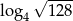 jest równa
jest równa
A) 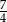 B)
B) 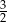 C) 7 D) 3,5
C) 7 D) 3,5
Niech 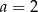 i
i 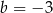 . Wartość wyrażenia
. Wartość wyrażenia 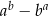 jest równa
jest równa
A) 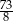 B)
B) 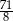 C)
C) 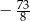 D)
D) 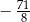
Funkcje liniowe  i
i 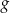 są określone wzorami
są określone wzorami 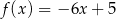 i
i 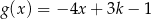 . Wykresy funkcji
. Wykresy funkcji 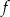 i
i 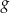 przecinają prostą
przecinają prostą 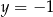 w tym samym punkcie. Stąd wynika, że
w tym samym punkcie. Stąd wynika, że
A) 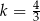 B)
B) 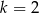 C)
C) 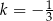 D)
D) 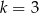
Na początku miesiąca deska snowboardowa kosztowała 4 500 zł. W drugiej dekadzie tego miesiąca cenę deski obniżono o 8%, a w trzeciej dekadzie cena tej deski została jeszcze raz obniżona, tym razem o 12%. Innych zmian ceny tej deski w tym miesiącu już nie było. Cena deski snowboardowej na koniec miesiąca była równa
A) 4 057,20 zł B) 4 086 zł C) 3 643,20 zł D) 3 600 zł
Informacja do zadań 7 – 9
Funkcja kwadratowa 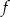 jest określona wzorem
jest określona wzorem 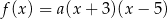 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 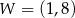 .
.
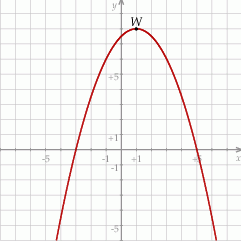
Współczynnik  we wzorze funkcji
we wzorze funkcji 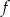 jest równy
jest równy
A) 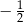 B) 2 C)
B) 2 C) 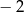 D)
D) 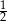
Największa wartość funkcji 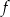 w przedziale
w przedziale 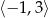 jest równa
jest równa
A) 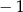 B) 0 C) 8 D) 6
B) 0 C) 8 D) 6
Osią symetrii paraboli będącej wykresem funkcji 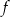 jest prosta o równaniu
jest prosta o równaniu
A) 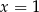 B)
B) 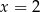 C)
C) 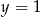 D)
D) 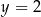
Jeśli 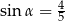 , to wartość wyrażenia
, to wartość wyrażenia 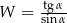 jest równa
jest równa
A) 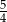 B)
B) 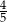 C)
C) 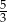 D)
D) 
Wskaż układ, który ma nieskończenie wiele rozwiązań.
A) 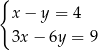 B)
B) 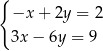 C)
C) 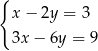 D)
D) 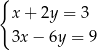
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 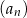 , określonego dla
, określonego dla 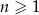 , wyraża się wzorem
, wyraża się wzorem 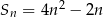 , zatem
, zatem
A) 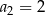 B)
B) 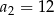 C)
C) 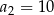 D)
D) 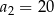
Proste o równaniach 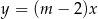 oraz
oraz 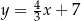 przecinają się w jednym punkcie Wtedy
przecinają się w jednym punkcie Wtedy
A) 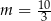 B)
B) 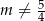 C)
C) 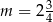 D)
D) 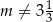
Punkt 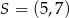 jest środkiem odcinka
jest środkiem odcinka 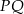 , którego koniec
, którego koniec 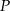 leży na osi
leży na osi 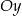 , a koniec
, a koniec 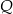 – na osi
– na osi 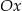 . Wynika stąd, że
. Wynika stąd, że
A) 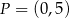 i
i 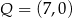 B)
B) 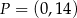 i
i 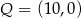
C) 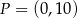 i
i 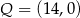 D)
D) 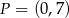 i
i 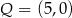
Punkty 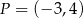 i
i 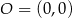 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem jaki tworzy ta prosta z ujemną półosią
jest kątem jaki tworzy ta prosta z ujemną półosią 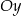 (zobacz rysunek).
(zobacz rysunek).
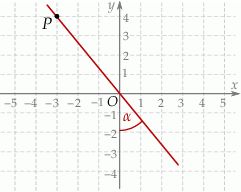
Wtedy tangens kąta  jest równy
jest równy
A) 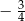 B)
B) 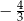 C)
C) 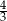 D)
D) 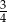
W ciągu arytmetycznym czwarty wyraz jest równy 13, a jedenasty jest równy 34. Różnica tego ciągu jest równa
A) 3 B) 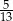 C) 21 D)
C) 21 D) 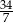
Punkty 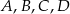 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 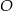 . Kąt środkowy
. Kąt środkowy 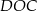 ma miarę
ma miarę 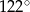 (zobacz rysunek).
(zobacz rysunek).
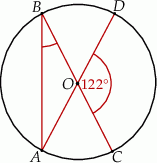
Miara kąta 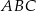 jest równa
jest równa
A) 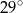 B)
B) 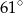 C)
C) 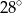 D)
D) 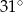
Przekątne trapezu 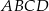 , w którym
, w którym 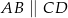 przecinają się w punkcie
przecinają się w punkcie 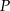 w ten sposób, że
w ten sposób, że 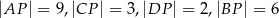 oraz
oraz 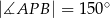 . Pole tego trapezu jest równe
. Pole tego trapezu jest równe
A) 32 B) 24 C) 18 D) 16
Pierwszy wyraz ciągu geometrycznego jest równy 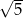 , a iloraz
, a iloraz 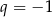 . Suma 1001 wyrazów tego ciągu jest równa
. Suma 1001 wyrazów tego ciągu jest równa
A) 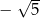 B) 0 C)
B) 0 C) 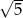 D)
D) 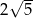
Pierwiastki trójmianu kwadratowego są liczbami przeciwnymi. Te warunki spełnia trójmian
A) 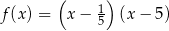 B)
B) 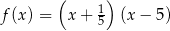
C) 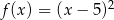 D)
D) 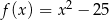
Ile jest wszystkich liczb naturalnych mniejszych od 500 utworzonych z cyfr: 1, 3, 5, 7, 9 (cyfry mogą się powtarzać)?
A) 125 B) 80 C) 75 D) 50
W prostokątnym układzie współrzędnych na płaszczyźnie parę prostych prostopadłych opisują równania
A) 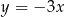 i
i 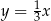 B)
B) 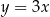 i
i 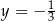
C) 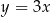 i
i 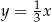 D)
D) 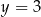 i
i 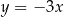
Punkty 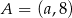 i
i 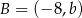 są końcami średnicy okręgu o środku
są końcami średnicy okręgu o środku 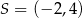 . Wtedy
. Wtedy
A) 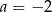 B)
B) 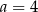 C)
C) 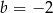 D)
D) 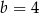
Ile liczb wymiernych znajduje się wśród liczb
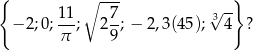
A) 2 B) 3 C) 4 D) 5
Dwa stożki o takich samych podstawach połączono podstawami w taki sposób jak na rysunku. Stosunek wysokości tych stożków jest równy 3 : 4. Objętość stożka o dłuższej wysokości jest równa 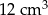 .
.
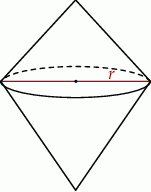
Objętość bryły utworzonej z połączonych stożków jest równa
A) 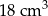 B)
B) 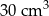 C)
C) 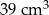 D)
D) 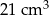
Losujemy jeden wierzchołek i jedną ścianę sześcianu. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowany wierzchołek jest wierzchołkiem wylosowanej ściany jest równe
A) 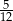 B)
B) 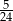 C)
C) 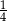 D)
D) 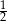
Na rysunku przedstawiono siatkę czworościanu foremnego.
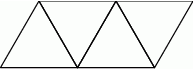
Jeżeli pole powierzchni całkowitej tego czworościanu jest równe 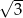 , to suma długości jego krawędzi jest równa
, to suma długości jego krawędzi jest równa
A) 9 B) 6 C) 4 D) 3
W grupie 50 kobiet i 50 mężczyzn przeprowadzono ankietę, w której zadano pytanie o liczbę książek przeczytanych w ostatnim roku. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba książek | 0 | 1 | 2 | 3 | 4 | 5 |
| Liczba osób | 23 | 14 | 28 | 17 | 11 | 7 |
W trakcie analizy tych danych zauważono, że kobiety przeczytały średnio o jedną książkę więcej niż mężczyźni. Średnia liczba przeczytanych książek przez jedną ankietowaną kobietę jest równa
A) 1,5 B) 1 C) 2 D) 2,5
Zadania otwarte
Rozwiąż nierówność 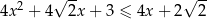 .
.
Wykaż, że dla dowolnych liczb rzeczywistych 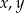 prawdziwa jest nierówność
prawdziwa jest nierówność
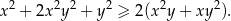
W pierwszej urnie znajdują się 4 kule białe i 13 kul czarnych. W drugiej urnie znajduje się 17 kul białych i 26 kul czarnych. Ile kul białych należy przełożyć z drugiej urny do pierwszej, aby wylosowanie kuli białej z obu urn było jednakowo prawdopodobne?
Punkt 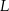 leży na boku
leży na boku 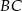 kwadratu
kwadratu 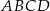 oraz
oraz 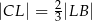 . Punkt
. Punkt 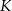 leży na przekątnej
leży na przekątnej 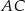 i odcinek
i odcinek 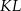 jest prostopadły do
jest prostopadły do 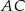 (zobacz rysunek).
(zobacz rysunek).
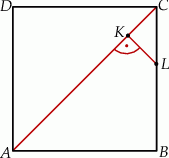
Wykaż, że 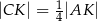 .
.
Punkty 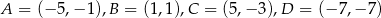 są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
Wszystkie wyrazy ciągu geometrycznego 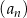 , określonego dla
, określonego dla 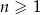 , są dodatnie. Wyrazy tego ciągu spełniają warunek
, są dodatnie. Wyrazy tego ciągu spełniają warunek 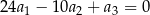 . Oblicz iloraz
. Oblicz iloraz 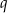 tego ciągu należący do przedziału
tego ciągu należący do przedziału 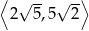 .
.
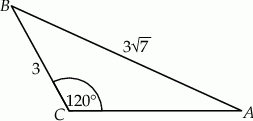
Dany jest trójkąt rozwartokątny 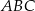 , w którym
, w którym 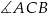 ma miarę
ma miarę 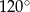 . Ponadto wiadomo, że
. Ponadto wiadomo, że 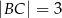 i
i 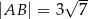 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta
(zobacz rysunek). Oblicz długość trzeciego boku trójkąta 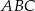 .
.