/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 2 marca 2019 Czas pracy: 170 minut
Zadania zamknięte
Cena towaru bez podatku VAT wynosi 240 zł. Ten sam towar wraz z podatkiem VAT i 8% rabatem handlowym kosztuje 231,84 zł. Jaką stawką VAT opodatkowano ten towar?
A) 5% B) 8% C) 23% D) 105%
Dane są liczby 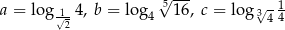 . Liczby te spełniają warunek
. Liczby te spełniają warunek
A) 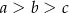 B)
B) 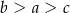 C)
C) 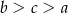 D)
D) 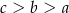
Dane są liczby 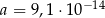 oraz
oraz 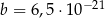 . Wtedy iloraz
. Wtedy iloraz 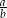 jest równy
jest równy
A) 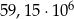 B)
B) 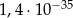 C)
C) 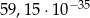 D)
D) 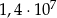
Wskaż liczbę spełniającą nierówność 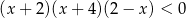 .
.
A) 1 B) 3 C) 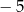 D)
D) 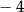
Liczba 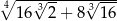 jest równa
jest równa
A) 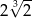 B)
B) 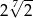 C)
C) 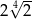 D)
D) 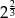
Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi  i
i 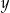 .
.
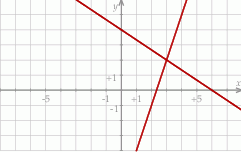
Wskaż ten układ
A) 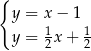 B)
B) 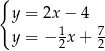 C)
C) 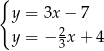 D)
D) 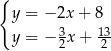
Równanie 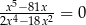
A) ma dwa rozwiązania B) ma trzy rozwiązania
C) nie ma rozwiązań D) ma jedno rozwiązanie
Liczba 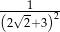 jest równa
jest równa
A) 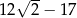 B)
B) 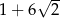 C)
C) 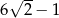 D)
D) 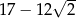
Funkcja 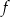 jest określona wzorem
jest określona wzorem 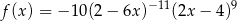 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 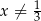 . Wartość funkcji
. Wartość funkcji 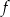 dla argumentu 2019 jest taka sama jak
dla argumentu 2019 jest taka sama jak 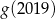 jeżeli
jeżeli
A) 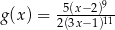 B)
B) 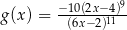
C) 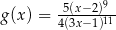 D)
D) 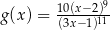
Punkt 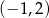 należy do wykresu funkcji
należy do wykresu funkcji 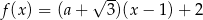 . Wynika stąd, że
. Wynika stąd, że
A) 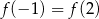 B)
B) 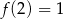 C)
C) 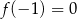 D)
D) 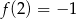
Dany jest ciąg 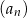 określony wzorem
określony wzorem 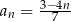 dla
dla 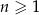 . Ciąg ten jest
. Ciąg ten jest
A) geometryczny i jego iloraz jest równy 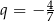 .
.
B) geometryczny i jego iloraz jest równy 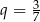 .
.
C) arytmetyczny i jego różnica jest równa 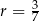 .
.
D) arytmetyczny i jego różnica jest równa 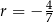 .
.
Gdy przesuniemy wykres funkcji 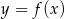 o 2 jednostki w prawo i 3 jednostki w górę, to otrzymamy wykres funkcji
o 2 jednostki w prawo i 3 jednostki w górę, to otrzymamy wykres funkcji 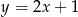 . Zatem
. Zatem
A) 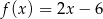 B)
B) 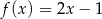 C)
C) 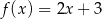 D)
D) 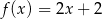
Wszystkie wyrazy ciągu geometrycznego 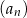 określonego dla
określonego dla 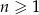 są dodatnie i
są dodatnie i 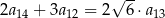 . Stąd wynika, że iloraz
. Stąd wynika, że iloraz 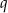 tego ciągu jest równy
tego ciągu jest równy
A) 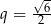 B)
B) 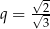 C)
C) 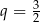 D)
D) 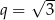
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 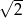 . Zatem
. Zatem
A) 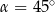 B)
B) 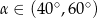 C)
C) 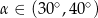 D)
D) 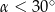
Dany jest trójkąt o bokach długości 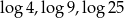 . Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
. Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A) 2, 3, 5 B) 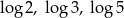 C)
C) 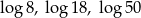 D) 4, 9, 25
D) 4, 9, 25
Liczba 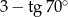 jest
jest
A) ujemna. B) dodatnia, ale mniejsza od 0,3.
C) większa od 0,3, ale mniejsza od 0,8. D) większa od 0,8.
Kąt wpisany oparty na łuku okręgu długości 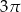 ma miarę
ma miarę 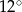 . Jakie jest pole koła ograniczonego tym okręgiem?
. Jakie jest pole koła ograniczonego tym okręgiem?
A) 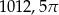 B)
B) 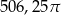 C)
C) 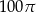 D)
D) 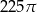
Różnica miar dwóch przeciwległych kątów deltoidu jest równa 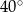 . Suma miar dwóch sąsiednich kątów tego deltoidu może być równa
. Suma miar dwóch sąsiednich kątów tego deltoidu może być równa
A) 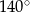 B)
B) 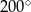 C)
C) 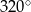 D)
D) 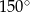
Proste o równaniach 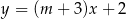 i
i 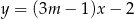 są równoległe, gdy
są równoległe, gdy
A) 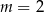 B)
B) 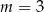 C)
C) 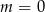 D)
D) 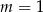
Objętość walca, w którym wysokość jest trzykrotnie krótsza od promienia podstawy, jest równa 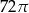 . Zatem promień podstawy tego walca ma długość:
. Zatem promień podstawy tego walca ma długość:
A) 4 B) 8 C) 2 D) 6
Punkt 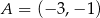 jest końcem odcinka
jest końcem odcinka 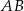 , a punkt
, a punkt 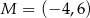 jest środkiem tego odcinka. Długość odcinka
jest środkiem tego odcinka. Długość odcinka 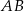 jest równa
jest równa
A) 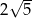 B)
B) 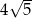 C)
C) 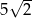 D)
D) 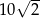
W zestawie 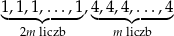 jest
jest 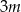 liczb (
liczb (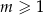 ), w tym
), w tym 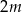 liczb 1 i
liczb 1 i 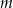 liczb 4. Odchylenie standardowe tego zestawu liczb jest równe
liczb 4. Odchylenie standardowe tego zestawu liczb jest równe
A) 2 B) 1 C) 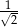 D)
D) 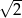
Obwód podstawy ostrosłupa prawidłowego siedmiokątnego jest równy 33,6 cm, a długość jego krawędzi bocznej jest równa 2,5 cm. Pole powierzchni bocznej tego ostrosłupa jest równe
A) 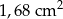 B)
B) 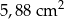 C)
C) 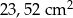 D)
D) 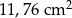
Maturzysta na rozwiązanie testu składającego się z 34 zadań przeznaczył 169 minut, przy czym na rozwiązanie każdego z 9 zadań otwartych przeznaczył trzy razy więcej czasu niż na rozwiązanie każdego z zdań zamkniętych. Średnia liczba sekund przeznaczonych na jedno zadanie zamknięte jest równa
A) 180 B) 205 C) 195 D) 170
W pudełku znajdują się dwie kule: niebieska i czerwona. Dziewięciokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie osiem z wylosowanych kul jest tego samego koloru jest równe
A) 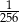 B)
B) 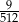 C)
C) 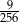 D)
D) 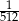
Zadania otwarte
Rozwiąż nierówność 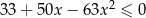 .
.
Rozwiąż równanie 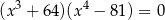 .
.
Udowodnij, że dla dowolnych liczb rzeczywistych 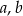 prawdziwa jest nierówność
prawdziwa jest nierówność
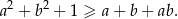
W ciągu arytmetycznym 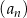 , określonym dla
, określonym dla 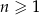 , suma 221 początkowych wyrazów jest równa 1547. Oblicz sumę
, suma 221 początkowych wyrazów jest równa 1547. Oblicz sumę 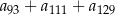 .
.
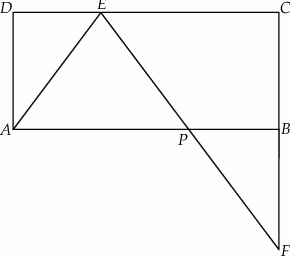
Dany jest prostokąt 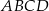 . Na boku
. Na boku 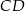 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 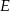 , że
, że 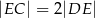 , a na przedłużeniu boku
, a na przedłużeniu boku 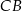 wybrano taki punkt
wybrano taki punkt 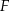 , że
, że 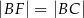 . Niech
. Niech 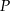 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 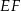 z prostą
z prostą 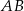 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 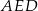 i
i 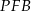 są przystające.
są przystające.
Losujemy jedną liczbę całkowitą z przedziału 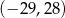 i jedną liczbę całkowitą z przedziału
i jedną liczbę całkowitą z przedziału 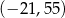 . Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest ujemny. Wynik podaj w postaci ułamka nieskracalnego.
. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest ujemny. Wynik podaj w postaci ułamka nieskracalnego.
W ostrosłupie prawidłowym trójkątnym 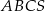 pole powierzchni bocznej jest trzy razy większe od pola podstawy. Oblicz sinus kąta nachylenia ściany bocznej tego ostrosłupa do płaszczyzny jego podstawy.
pole powierzchni bocznej jest trzy razy większe od pola podstawy. Oblicz sinus kąta nachylenia ściany bocznej tego ostrosłupa do płaszczyzny jego podstawy.
Oblicz pole rombu o obwodzie 68 cm, w którym długości przekątnych różnią się o 14 cm.
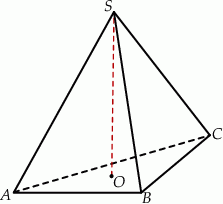
Punkty 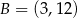 ,
, 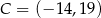 i
i 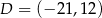 są kolejnymi wierzchołkami trapezu równoramiennego
są kolejnymi wierzchołkami trapezu równoramiennego 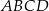 , który nie jest równoległobokiem, i w którym
, który nie jest równoległobokiem, i w którym 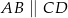 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 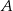 tego trapezu.
tego trapezu.

