/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 15 marca 2014 Czas pracy: 170 minut
Zadania zamknięte
Liczba 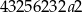 jest podzielna przez 4 jeżeli
jest podzielna przez 4 jeżeli
A) 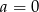 B)
B) 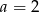 C)
C) 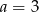 D)
D) 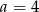
Dodatnia liczba  stanowi 30% liczby
stanowi 30% liczby 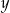 . Wówczas
. Wówczas
A) 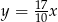 B)
B) 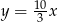 C)
C) 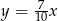 D)
D) 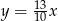
Liczba 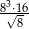 jest równa
jest równa
A) 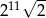 B)
B) 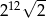 C)
C) 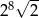 D)
D) 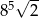
Rozwiązaniem układu równań 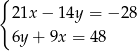 jest para liczb
jest para liczb
A) 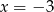 i
i 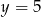 B)
B) 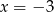 i
i 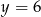 C)
C) 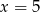 i
i 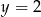 D)
D) 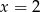 i
i 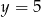
Liczba 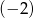 jest pierwiastkiem równania
jest pierwiastkiem równania 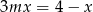 . Wtedy
. Wtedy
A) 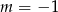 B)
B) 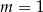 C)
C) 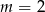 D)
D) 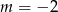
Wyrażenie 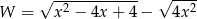 dla
dla 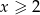 przyjmuje postać
przyjmuje postać
A) 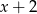 B)
B) 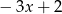 C)
C) 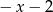 D)
D) 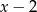
Prosta 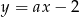 jest równoległa do prostej
jest równoległa do prostej 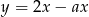 . Wtedy
. Wtedy
A) 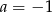 B)
B) 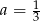 C)
C) 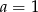 D)
D) 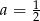
Do zbioru rozwiązań nierówności 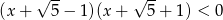 należy liczba
należy liczba
A) 0 B) 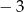 C)
C) 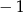 D) 3
D) 3
Kąt  jest kątem ostrym oraz
jest kątem ostrym oraz 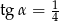 . Zatem
. Zatem
A) 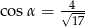 B)
B) 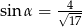 C)
C) 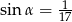 D)
D) 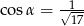
Na poniższych rysunkach przedstawiono wykresy funkcji 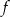 i
i 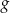 .
.
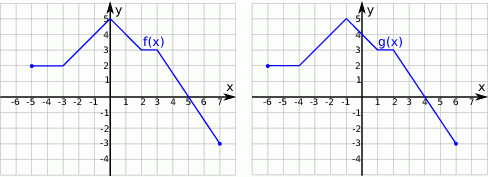
Funkcja 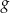 jest określona wzorem
jest określona wzorem
A) 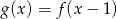 B)
B) 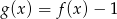 C)
C) 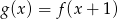 D)
D) 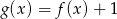
Wielomian 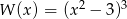 jest równy wielomianowi
jest równy wielomianowi
A) 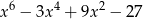
B) 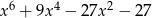
C) 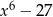
D) 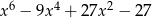
Dany jest ciąg 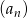 o wyrazie ogólnym
o wyrazie ogólnym 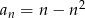 , gdzie
, gdzie 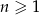 . Wówczas
. Wówczas
A) 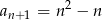 B)
B) 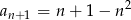 C)
C) 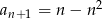 D)
D) 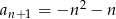
Prostokąt 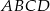 o przekątnej długości
o przekątnej długości 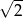 jest podobny do prostokąta o bokach długości 1 i 7. Obwód prostokąta
jest podobny do prostokąta o bokach długości 1 i 7. Obwód prostokąta 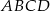 jest równy
jest równy
A) 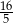 B)
B) 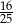 C) 80 D) 16
C) 80 D) 16
Ciągiem geometrycznym jest ciąg określony wzorem
A) 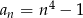 B)
B) 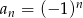 C)
C) 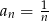 D)
D) 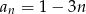
Ile jest wszystkich liczb naturalnych czterocyfrowych podzielnych przez 5?
A) 2000 B) 1800 C) 1000 D) 900
Dany jest okrąg o środku w punkcie 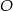 . Prosta
. Prosta 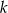 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 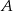 .
.
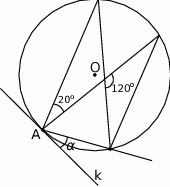
Miara kąta  jest równa
jest równa
A) 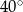 B)
B) 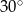 C)
C) 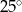 D)
D) 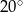
Funkcja 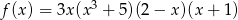 ma dokładnie
ma dokładnie
A) 1 pierwiastek B) 2 pierwiastki C) 3 pierwiastki D) 4 pierwiastki
Obwód równoległoboku 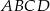 o wierzchołkach
o wierzchołkach 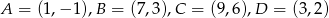 jest równy
jest równy
A) 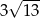 B)
B) 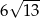 C)
C) 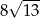 D)
D) 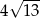
Liczba krawędzi graniastosłupa jest o 8 większa od liczby jego ścian. Ile wierzchołków ma ten graniastosłup?
A) 5 B) 15 C) 10 D) 16
Piąty wyraz ciągu arytmetycznego jest równy 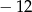 , a różnica tego ciągu jest równa
, a różnica tego ciągu jest równa 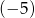 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 8 B) 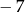 C)
C) 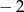 D) 3
D) 3
Pole koła ograniczonego okręgiem 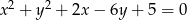 jest równe
jest równe
A) 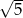 B)
B) 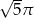 C)
C) 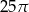 D)
D) 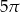
Mediana uporządkowanego niemalejąco zestawu sześciu liczb: 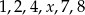 jest równa 5. Wtedy
jest równa 5. Wtedy
A) 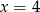 B)
B) 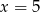 C)
C) 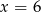 D)
D) 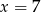
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo dwukrotnego otrzymania liczby oczek różnej od 5 jest równe
A)  B)
B) 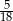 C)
C) 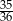 D)
D) 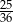
Objętość stożka o wysokości 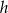 i promieniu podstawy cztery razy mniejszym od wysokości jest równa
i promieniu podstawy cztery razy mniejszym od wysokości jest równa
A) 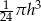 B)
B) 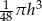 C)
C) 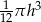 D)
D) 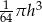
Liczba 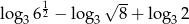 jest równa
jest równa
A) 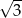 B)
B) 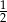 C)
C) 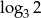 D)
D) 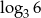
Zadania otwarte
Kąt  jest ostry i
jest ostry i 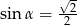 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 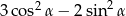 .
.
Rozwiąż równanie 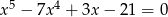 .
.
Udowodnij, że jeżeli liczby niezerowe 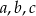 spełniają warunek
spełniają warunek 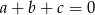 to
to
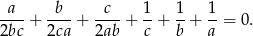
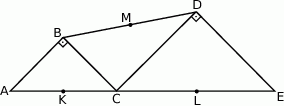
Trójkąty 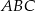 i
i 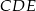 są równoramienne i prostokątne. Punkty
są równoramienne i prostokątne. Punkty 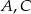 i
i 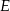 leżą na jednej prostej, a punkty
leżą na jednej prostej, a punkty 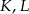 i
i 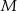 są środkami odcinków
są środkami odcinków 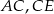 i
i 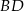 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 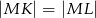 .
.
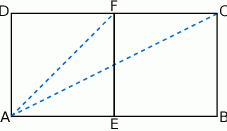
Odcinek 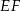 łączący środki dwóch dłuższych boków prostokąta
łączący środki dwóch dłuższych boków prostokąta 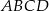 dzieli go na dwa kwadraty, przy czym przekątna prostokąta jest o 3 dłuższa od przekątnej kwadratu. Oblicz pole prostokąta
dzieli go na dwa kwadraty, przy czym przekątna prostokąta jest o 3 dłuższa od przekątnej kwadratu. Oblicz pole prostokąta 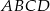 .
.
Na rysunku przedstawiony jest wykres funkcji 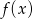 określonej dla
określonej dla 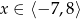 .
.
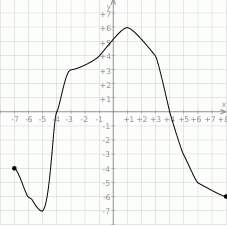
Odczytaj z wykresu i zapisz:
- najmniejszą wartość funkcji
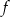 ,
, - zbiór rozwiązań nierówności
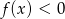 .
.
Oblicz objętość i pole powierzchni bocznej ostrosłupa prawidłowego sześciokątnego o krawędzi podstawy 2 cm i krawędzi bocznej 6 cm.
W pewnej szkole 47% uczniów uczęszcza na kółko plastyczne, a 65% uczniów uczęszcza na kółko muzyczne. Wiadomo ponadto, że 30% uczniów uczęszcza na obydwa kółka. Oblicz prawdopodobieństwo, że losowy wybrany uczeń tej szkoły nie uczęszcza na żadne z tych kółek.
Wierzchołki trapezu 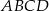 mają współrzędne:
mają współrzędne: 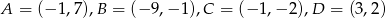 . Napisz równanie okręgu, który jest styczny do podstawy
. Napisz równanie okręgu, który jest styczny do podstawy 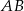 tego trapezu, a jego środek jest punktem przecięcia się przekątnych trapezu
tego trapezu, a jego środek jest punktem przecięcia się przekątnych trapezu 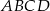 .
.

