/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 23 marca 2013 Czas pracy: 180 minut

Zadanie 1
(4 pkt)

Wykres funkcji 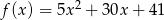2 f (x) = 5x + 30x + 4 1 przekształcono w symetrii względem prostej 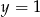y = 1 i otrzymano wykres funkcji 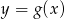y = g (x ) . Wyznacz wzór funkcji g .

Zadanie 2
(5 pkt)

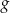Wyznacz cztery kolejne liczby całkowite takie, że sześcian największej z nich jest równy sumie sześcianów trzech pozostałych liczb.

Zadanie 3
(4 pkt)

Wielomian 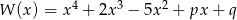W (x) = x4 + 2x3 − 5x2 + px + q jest podzielny przez dwumian 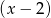(x− 2) , a przy dzieleniu przez 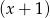(x+ 1) daje resztę 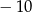− 10 . Wyznacz p i q .

Zadanie 4
(3 pkt)

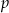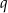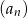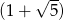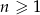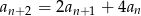Iloraz ciągu geometrycznego (an) jest równy √ -- (1+ 5) . Uzasadnij, że dla każdej liczby naturalnej n ≥ 1 prawdziwy jest wzór a = 2a + 4a n+ 2 n+ 1 n .

Zadanie 5
(5 pkt)

Wyznacz wszystkie rozwiązania równania 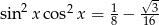2 2 1 √-3 sin x cos x = 8 − 16 należące do przedziału ⟨0,π ⟩ .

Zadanie 6
(4 pkt)

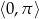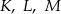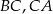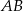Punkty K, L, M są środkami boków BC ,CA i AB trójkąta 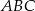ABC . Wykaż, że

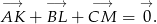
− → − → −→ → AK + BL + CM = 0.

Zadanie 7
(6 pkt)

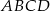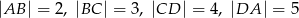Czworokąt ABCD jest wpisany w okrąg oraz |AB | = 2 , |BC | = 3, |CD | = 4, |DA | = 5 .

  • Oblicz co s∡BCD .
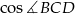  • Oblicz pole czworokąta ABCD .

Zadanie 8
(6 pkt)

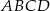Z punktu 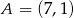A = (7,1) poprowadzono styczne do okręgu 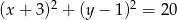(x + 3)2 + (y − 1)2 = 20 . Oblicz pole trójkąta 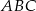ABC , gdzie 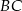BC jest odcinkiem łączącym punkty styczności.

Zadanie 9
(5 pkt)

Z liter 26 literowego alfabetu łacińskiego tworzymy czteroliterowe kody, przy czym każdy kod składa się z czterech różnych liter, które zostały wybrane z pewnych 6 kolejnych liter alfabetu. Ile jest takich kodów?

Zadanie 10
(4 pkt)

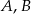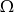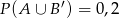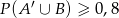Zdarzenia losowe A ,B są zawarte w Ω oraz P(A ∪ B′) = 0,2 . Wykaż, że P(A ′ ∪ B ) ≥ 0,8 .

Zadanie 11
(4 pkt)

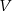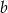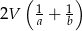Podstawą graniastosłupa prostego o objętości V jest równoległobok o bokach długości a i b . Wykaż, że pole powierzchni bocznej tego graniastosłupa jest nie mniejsze niż (1 1) 2V a + b .

Arkusz Wersja PDF
Rozwiązania