/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 9 kwietnia 2022 Czas pracy: 170 minut
Zadania zamknięte
Liczba 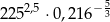 jest równa
jest równa
A) 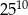 B)
B) 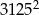 C)
C) 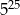 D)
D) 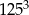
Cenę biurka obniżono o 10%, a następnie nową cenę obniżono o 30%. W wyniku obu tych zmian cena biurka zmniejszyła się w stosunku do ceny sprzed obu obniżek o
A) 43% B) 40% C) 37% D) 63%
Jeżeli 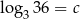 , to liczba
, to liczba 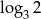 jest równa
jest równa
A) 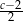 B)
B) 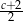 C)
C) 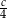 D)
D) 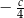
Dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 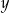 wyrażenie
wyrażenie 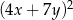 jest równe
jest równe
A) 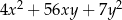 B)
B) 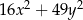 C)
C) 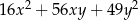 D)
D) 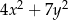
Różnica 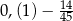 jest równa
jest równa
A) 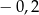 B)
B) 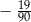 C)
C) 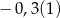 D)
D) 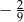
Liczba 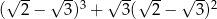 jest równa
jest równa
A) 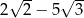 B)
B) 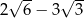 C)
C) 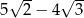 D)
D) 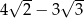
Jednym z rozwiązań równania 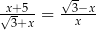 jest
jest
A) 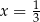 B)
B) 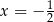 C)
C) 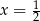 D)
D) 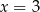
Funkcja 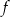 jest określona wzorem
jest określona wzorem 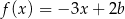 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Funkcje
. Funkcje 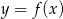 i
i 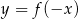 mają to samo miejsce zerowe. Wtedy
mają to samo miejsce zerowe. Wtedy
A) 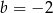 B)
B) 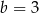 C)
C) 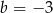 D)
D) 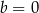
Przekątne 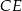 i
i 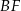 sześciokąta foremnego
sześciokąta foremnego 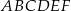 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 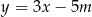 i
i 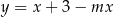 . Zatem
. Zatem
A) 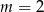 B)
B) 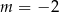 C)
C) 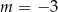 D)
D) 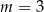
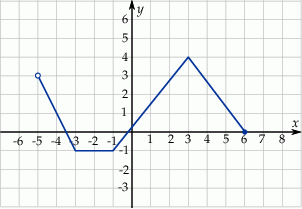
Dany jest wykres funkcji 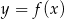 . Dziedziną
. Dziedziną 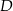 i zbiorem wartości
i zbiorem wartości 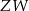 tej funkcji jest
tej funkcji jest
A) 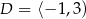 ,
, 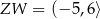 B)
B) 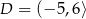 ,
, 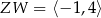
C) 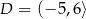 ,
, 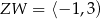 D)
D) 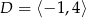 ,
, 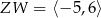
Punkt 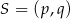 jest wierzchołkiem paraboli będącej wykresem funkcji
jest wierzchołkiem paraboli będącej wykresem funkcji 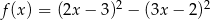 . Zatem
. Zatem
A) 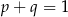 B)
B) 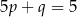 C)
C) 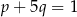 D)
D) 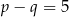
Kąt o mierze  jest ostry i
jest ostry i 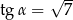 . Wtedy
. Wtedy
A) 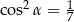 B)
B) 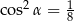 C)
C) 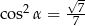 D)
D) 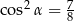
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 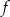 .
.
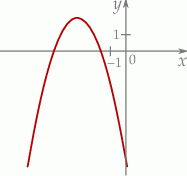
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 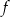 .
.
A) 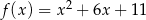 B)
B) 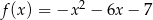
C) 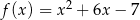 D)
D) 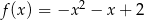
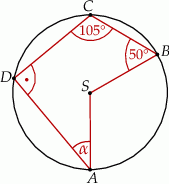
Na rysunku przedstawiono okrąg o środku 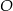 , który jest wpisany w trójkąt
, który jest wpisany w trójkąt 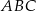 .
.
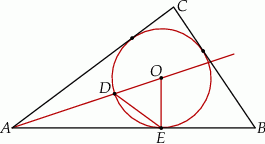
Okrąg ten przecina bok 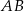 w punkcie
w punkcie 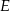 , a odcinek
, a odcinek 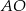 w punkcie
w punkcie 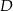 . Jeżeli
. Jeżeli 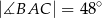 , to miara kąta
, to miara kąta 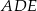 jest równa
jest równa
A) 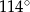 B)
B) 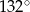 C)
C) 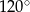 D)
D) 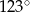
Trzywyrazowy ciąg 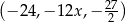 jest geometryczny i wszystkie jego wyrazy są ujemne. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są ujemne. Stąd wynika, że
A) 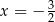 B)
B) 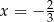 C)
C) 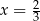 D)
D) 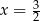
Wskaż największą liczbę całkowitą spełniającą nierówność 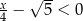 .
.
A) 5 B) 6 C) 7 D) 8
Dany jest trójkąt 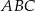 o bokach
o bokach 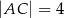 ,
, 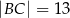 ,
, 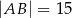 . Sinus kąta
. Sinus kąta 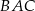 jest równy
jest równy  , a dwusieczne kątów
, a dwusieczne kątów 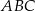 i
i 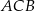 przecinają się w punkcie
przecinają się w punkcie 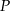 (zobacz rysunek).
(zobacz rysunek).
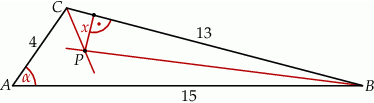
Odległość  punktu
punktu 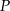 od prostej
od prostej 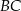 jest równa
jest równa
A) 2 B) 1 C)  D)
D) 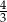
Przyprostokątna 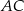 trójkąta prostokątnego
trójkąta prostokątnego 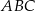 ma długość 14 oraz
ma długość 14 oraz 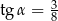 (zobacz rysunek).
(zobacz rysunek).
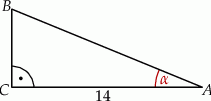
Pole tego trójkąta jest równe
A) 73,5 B) 36,75 C) 5,25 D) 37,3
Suma dwóch początkowych wyrazów ciągu arytmetycznego 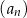 wynosi 7, a trzeci wyraz jest równy 5. Wówczas
wynosi 7, a trzeci wyraz jest równy 5. Wówczas
A) 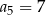 B)
B) 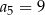 C)
C) 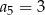 D)
D) 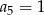
Przekątna 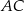 prostokąta
prostokąta 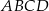 ma długość 104. Na boku
ma długość 104. Na boku 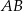 obrano punkt
obrano punkt 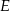 , na przekątnej
, na przekątnej 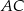 obrano punkt
obrano punkt 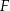 , a na boku
, a na boku 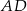 obrano punkt
obrano punkt 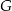 – tak, że czworokąt
– tak, że czworokąt 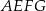 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 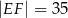 i
i 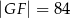 .
.
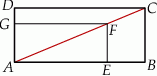
Obwód prostokąta 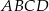 jest równy
jest równy
A) 272 B) 238 C) 221 D) 136
Punkty 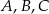 i
i 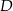 leżą na okręgu o środku
leżą na okręgu o środku 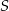 . Miary kątów
. Miary kątów 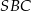 ,
, 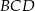 ,
, 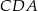 są równe odpowiednio:
są równe odpowiednio: 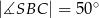 ,
, 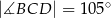 ,
, 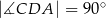 (zobacz rysunek).
(zobacz rysunek).
Wynika stąd, że miara  kąta
kąta 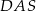 jest równa
jest równa
A) 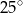 B)
B) 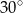 C)
C) 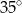 D)
D) 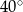
Szósty wyraz ciągu 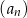 określonego wzorem
określonego wzorem 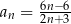 , gdzie
, gdzie 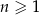 jest równy
jest równy
A) 2 B) 1 C) 12 D) 0,5
Obrazem prostej o równaniu 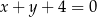 w symetrii osiowej względem prostej
w symetrii osiowej względem prostej 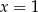 jest prosta o równaniu
jest prosta o równaniu
A) 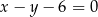 B)
B) 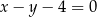 C)
C) 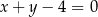 D)
D) 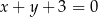
Podstawą graniastosłupa prostego jest romb, w którym miara kąta ostrego jest równa 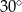 . Każda krawędź tego graniastosłupa ma długość równą 2 (zobacz rysunek).
. Każda krawędź tego graniastosłupa ma długość równą 2 (zobacz rysunek).
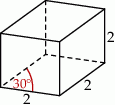
Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 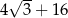 B)
B) 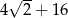 C) 18 D) 20
C) 18 D) 20
Punkty 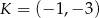 i
i 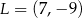 są środkami boków
są środkami boków 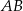 i
i 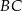 prostokąta
prostokąta 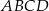 . Boki prostokąta
. Boki prostokąta 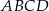 są równoległe do osi układu współrzędnych. Pole prostokąta
są równoległe do osi układu współrzędnych. Pole prostokąta 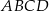 jest równe.
jest równe.
A) 48 B) 20 C) 192 D) 400
Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego jest 3 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy
A) 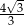 B)
B) 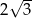 C)
C) 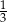 D)
D) 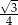
Pewnego dnia w klasie Ib było dwa razy więcej uczniów, niż w klasie Ia. Tego samego dnia dziewczynki stanowiły 40% uczniów klasy Ia, oraz 60% uczniów klasy Ib. Jeżeli tego dnia wylosujemy jednego ucznia z klas Ia i Ib, to prawdopodobieństwo wylosowania chłopca jest równe
A) 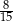 B)
B) 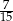 C)
C) 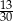 D)
D) 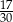
Średnia arytmetyczna pięciu liczb: 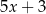 ,
, 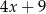 ,
, 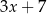 ,
, 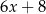 ,
, 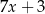 , jest równa 11. Wtedy
, jest równa 11. Wtedy  jest równe
jest równe
A) 1 B) 5 C) 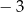 D)
D) 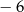
Zadania otwarte
Rozwiąż nierówność 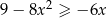 .
.
Wykaż, że dla wszystkich liczb rzeczywistych 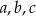 i
i 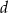 takich, że
takich, że 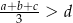 ,
, 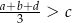 i
i 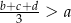 , prawdziwa jest nierówność
, prawdziwa jest nierówność
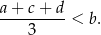
Dany jest ciąg arytmetyczny 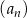 , określony dla wszystkich liczb naturalnych
, określony dla wszystkich liczb naturalnych 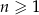 . Suma piętnastu początkowych wyrazów tego ciągu jest równa
. Suma piętnastu początkowych wyrazów tego ciągu jest równa 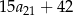 . Oblicz różnicę ciągu
. Oblicz różnicę ciągu 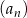 .
.
Kąt  jest ostry i spełnia warunek
jest ostry i spełnia warunek 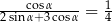 . Oblicz tangens kąta
. Oblicz tangens kąta  .
.
Kąt 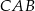 trójkąta prostokątnego
trójkąta prostokątnego 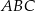 ma miarę
ma miarę 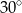 . Odcinek
. Odcinek 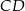 jest wysokością tego trójkąta opuszczoną na przeciwprostokątną
jest wysokością tego trójkąta opuszczoną na przeciwprostokątną 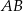 . Oblicz stosunek pól trójkątów
. Oblicz stosunek pól trójkątów 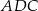 i
i 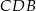 .
.
Rzucamy trzy razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w pierwszym rzucie otrzymamy dwa razy więcej oczek niż w trzecim rzucie.
Przekątna 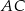 rombu
rombu 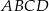 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 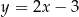 . Wierzchołki
. Wierzchołki 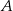 i
i 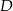 mają współrzędne
mają współrzędne 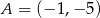 i
i 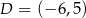 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 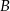 i
i 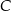 oraz pole rombu
oraz pole rombu 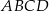 .
.

