/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom podstawowy 8 marca 2019 Czas pracy: 170 minut
Zadania zamknięte
Wśród liczb 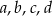 liczbą całkowitą jest
liczbą całkowitą jest
A) 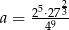 B)
B) 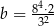 C)
C) 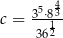 D)
D) 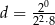
Jeżeli 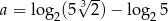 i
i 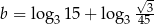 , to wartość wyrażenia
, to wartość wyrażenia 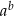 jest równa
jest równa
A) 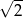 B)
B) 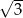 C) 9 D)
C) 9 D) 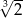
Oszacowano, że do malowania pokoju potrzeba 17 litrów farby. W rzeczywistości zużyto 20 litrów. Błąd względny szacowania wyrażony w procentach wynosi
A) 0,15% B) 15% C) 17,6% D) 85%
Cenę towaru dwukrotnie obniżano o 20%. W wyniku obniżek cena towaru wynosi 96 zł. Przed zmianami towar kosztował
A) 138,24 zł B) 144,00 zł C) 150,00 zł D) 160,00 zł
Funkcja 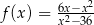
A) ma jedno miejsce zerowe 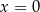
B) ma dwa miejsca zerowe: 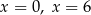
C) ma dwa miejsce zerowe: 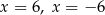
D) ma trzy miejsca zerowe: 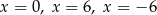
Na rysunku przedstawiono wykres funkcji określonej wzorem
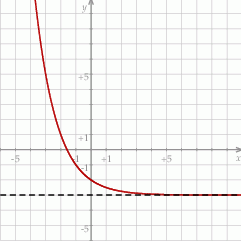
A) 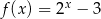 B)
B) 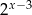 C)
C) 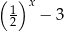 D)
D) 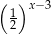
Wartość funkcji 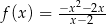 dla argumentu równego
dla argumentu równego 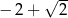 wynosi
wynosi
A) 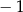 B)
B) 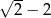 C)
C) 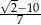 D)
D) 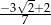
Dana jest funkcja liniowa 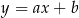 , o której wiadomo, że
, o której wiadomo, że 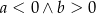 . Wykres tej funkcji przechodzi przez następujące ćwiartki układu współrzędnych
. Wykres tej funkcji przechodzi przez następujące ćwiartki układu współrzędnych
A) I, II, III B) I, II, IV C) II, III, IV D) I, III, IV
Maksymalnym przedziałem, w którym funkcja kwadratowa 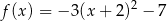 jest malejąca jest
jest malejąca jest
A) 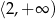 B)
B) 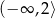 C)
C) 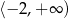 D)
D) 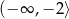
Dany jest ciąg 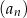 określony wzorem ogólnym
określony wzorem ogólnym 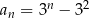 . Wyraz
. Wyraz 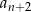 tego ciągu dla
tego ciągu dla 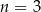 jest równy
jest równy
A) 3 B) 18 C) 27 D) 234
Pierwszy wyraz ciągu arytmetycznego wynosi 7, suma siedmiu początkowych wyrazów ciągu jest równa 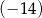 . Czwarty wyraz ciągu jest równy
. Czwarty wyraz ciągu jest równy
A) 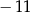 B)
B) 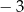 C)
C) 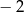 D) 16
D) 16
Za wykopanie pierwszego metra studni zapłacono 75 złotych. Wykopanie każdego następnego metra kosztowało dwa razy tyle co poprzedniego. Za wykopanie studni zapłacono 76725 złotych. Głębokość studni wynosiła
A) 7 m B) 8 m C) 9 m D) 10 m
Ramię końcowe kąta 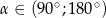 zawiera się w prostej
zawiera się w prostej 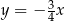 . Zatem
. Zatem
A) 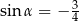 B)
B) 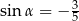 C)
C) 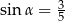 D)
D) 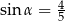
Kąt  jest kątem ostrym i
jest kątem ostrym i 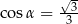 . Zatem
. Zatem
A) 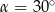 B)
B) 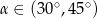 C)
C) 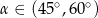 D)
D) 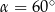
Dla ostrego kąta  wyrażenie
wyrażenie 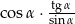 jest równe
jest równe
A) 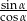 B)
B) 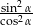 C)
C) 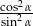 D)
D) 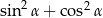
Punkty 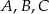 leżą na okręgu o środku
leżą na okręgu o środku 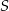 (rysunek),
(rysunek), 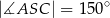 oraz
oraz  . Miara kąta
. Miara kąta  jest równa
jest równa
A) 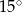 B)
B) 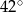 C)
C) 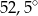 D)
D) 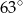
Punkty 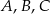 są punktami przecięcia paraboli o równaniu
są punktami przecięcia paraboli o równaniu 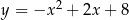 z osiami układu współrzędnych. Pole trójkąta
z osiami układu współrzędnych. Pole trójkąta 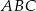 jest równe
jest równe
A) 8 B) 9 C) 24 D) 27
Dane są okręgi styczne wewnętrznie o środkach 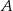 i
i 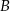 . Wiadomo, że promień jednego okręgu jest trzy razy dłuższy od promienia drugiego okręgu i
. Wiadomo, że promień jednego okręgu jest trzy razy dłuższy od promienia drugiego okręgu i 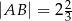 . Promienie tych okręgów mają długość
. Promienie tych okręgów mają długość
A) 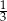 i 3 B)
i 3 B) 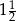 i
i 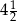 C)
C) 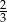 i 2 D)
i 2 D) 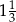 i 4
i 4
Proste o równaniach 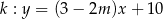 i
i 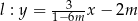 są prostopadłe dla
są prostopadłe dla
A) 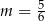 B)
B) 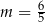 C)
C) 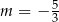 D)
D) 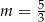
Punkty 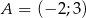 ,
, 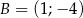 ,
, 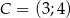 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 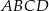 . Równanie prostej zawierającej bok
. Równanie prostej zawierającej bok 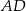 tego równoległoboku ma postać
tego równoległoboku ma postać
A) 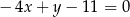 B)
B) 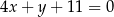
C) 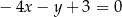 D)
D) 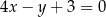
Dany jest odcinek 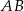 , gdzie
, gdzie 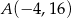 ,
, 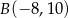 . Punkt
. Punkt 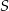 jest środkiem odcinka
jest środkiem odcinka 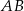 . Obrazem punktu
. Obrazem punktu 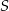 w symetrii względem osi
w symetrii względem osi 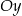 jest punkt
jest punkt
A) 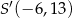 B)
B) 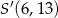 C)
C)  D)
D) 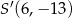
Przekrój osiowy stożka jest trójkątem równoramiennym o ramieniu długości 12. Kąt rozwarcia stożka ma miarę 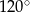 . Objętość stożka wynosi
. Objętość stożka wynosi
A) 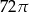 B)
B) 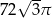 C)
C) 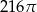 D)
D) 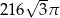
Przekątne dzielą równoległobok na cztery trójkąty
A) przystające B) podobne C) o równych polach D) o równych obwodach
Ze zbioru 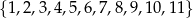 losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę
losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę 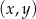 , gdzie
, gdzie  jest pierwszą wylosowaną liczbą,
jest pierwszą wylosowaną liczbą, 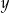 jest drugą wylosowaną liczbą. Wszystkich par
jest drugą wylosowaną liczbą. Wszystkich par 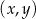 takich, że suma
takich, że suma 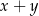 jest liczbą parzystą jest
jest liczbą parzystą jest
A) 20 B) 25 C) 50 D) 61
Wojtek notował temperaturę powietrza o godzinie 12.00 w pięciu kolejnych dniach stycznia. Otrzymał następujące wyniki:
| Data | 15.01 | 16.01 | 17.01 | 18.01 | 19.01 |
| Temperatura | 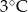 | 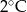 | 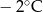 | 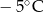 | 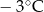 |
Odchylenie standardowe od średniej temperatury w tych dniach, z dokładnością do 0,1 wynosi
A) 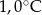 B)
B) 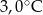 C)
C) 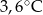 D)
D) 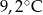
Zadania otwarte
Na rysunku przedstawiony jest wykres funkcji 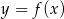 . Podaj zbiór wartości funkcji
. Podaj zbiór wartości funkcji 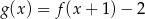 .
.
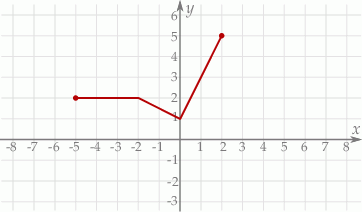
Rozwiąż nierówność 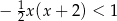 .
.
Udowodnij, że reszta z dzielenia sumy kwadratów dwóch kolejnych liczb naturalnych niepodzielnych przez 3, przy dzieleniu przez 18 jest równa 5.
Rozwiąż równanie 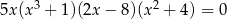 .
.
W dwóch pojemnikach znajdują się ponumerowane kule. W pierwszym pojemniku są kule z numerami: 1, 2, 3, 4, 5, w drugim z numerami: 4, 5, 6, 7, 8, 9. Losujemy po jednej kuli z każdego pojemnika i tworzymy liczbę dwucyfrową. Numer kuli wylosowanej z pierwszego pojemnika jest cyfrą dziesiątek, numer kuli wylosowanej z drugiego pojemnika jest cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że utworzona liczba jest podzielna przez 4.
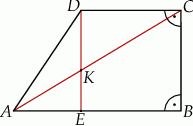
W trapezie prostokątnym 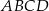 (rysunek) punkt
(rysunek) punkt 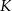 jest punktem przecięcia wysokości
jest punktem przecięcia wysokości 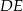 i przekątnej
i przekątnej 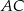 tego trapezu. Wiedząc, że
tego trapezu. Wiedząc, że 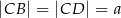 i
i 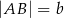 wykaż, że pole
wykaż, że pole 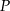 czworokąta
czworokąta 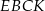 jest równe
jest równe 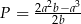 .
.
Punkty 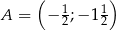 ,
, 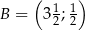 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 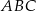 o podstawie
o podstawie 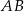 . Ramię
. Ramię 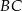 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 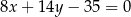 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 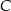 i pole tego trójkąta.
i pole tego trójkąta.
Funkcja kwadratowa 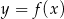 przyjmuje wartości ujemne tylko dla
przyjmuje wartości ujemne tylko dla 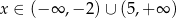 , a jej zbiorem wartości jest przedział
, a jej zbiorem wartości jest przedział 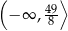 . Zapisz wzór funkcji kwadratowej
. Zapisz wzór funkcji kwadratowej 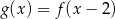 w postaci ogólnej.
w postaci ogólnej.
Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 8 cm, a jego wysokość 12 cm. Połączono środki dwóch sąsiednich krawędzi dolnej podstawy oraz najbardziej odległy od tego odcinka wierzchołek górnej podstawy. Oblicz pole otrzymanego trójkąta.

