/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 16 kwietnia 2016 Czas pracy: 170 minut
Zadania zamknięte
Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności 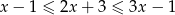 .
.

Jeśli 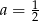 ,
, 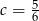 i
i 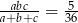 , to
, to 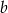 jest równe
jest równe
A) 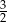 B)
B) 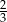 C)
C) 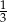 D)
D) 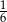
Przy 23-procentowej stawce podatku VAT cena brutto lodówki jest równa 1574,4 zł. Jaka jest cena netto tej lodówki?
A) 985,6 zł B) 1936,512 zł C) 1280 zł D) 1290,49 zł
Liczba 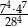 jest równa
jest równa
A) 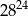 B)
B) 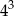 C)
C) 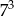 D)
D) 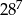
Układ równań 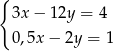 opisuje w układzie współrzędnych na płaszczyźnie
opisuje w układzie współrzędnych na płaszczyźnie
A) zbiór pusty.
B) dokładnie jeden punkt.
C) dokładnie dwa różne punkty.
D) zbiór nieskończony.
Która z poniższych równości jest prawdziwa dla każdej liczby rzeczywistej  ?
?
A) 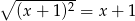 B)
B) 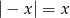 C)
C) 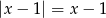 D)
D) 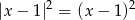
Wartość wyrażenia 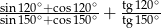 jest równa
jest równa
A) 4 B) 0 C) 1 D) 2
Jeżeli 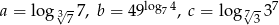 to
to
A) 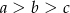 B)
B) 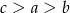 C)
C) 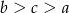 D)
D) 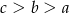
Na wykresie funkcji liniowej określonej wzorem 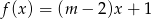 leży punkt
leży punkt 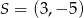 . Zatem
. Zatem
A) 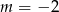 B)
B) 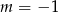 C)
C) 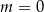 D)
D) 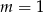
Funkcja 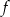 jest określona wzorem
jest określona wzorem 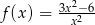 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 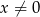 . Wówczas wartość funkcji
. Wówczas wartość funkcji 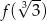 jest równa
jest równa
A) 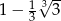 B)
B) 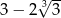 C)
C) 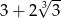 D)
D) 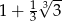
Liczba niewymiernych rozwiązań równania 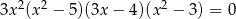 jest równa
jest równa
A) 1 B) 2 C) 4 D) 5
Wskaż wzór funkcji, która przecina osie układu współrzędnych w 3 punktach.
A) 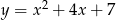
B) 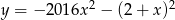
C) 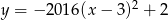
D) 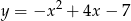
Iloraz nieskończonego ciągu geometrycznego 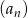 jest równy
jest równy 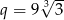 . Wynika stąd, że
. Wynika stąd, że
A) 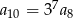 B)
B) 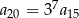 C)
C) 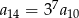 D)
D) 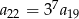
Wszystkie dwucyfrowe liczby naturalne podzielne przez 8 tworzą rosnący ciąg arytmetyczny. Jedenastym wyrazem tego ciągu jest liczba
A) 92 B) 72 C) 88 D) 96
Rozwiązaniem nierówności 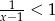 jest zbiór
jest zbiór
A) 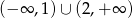
B) 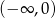
C) 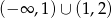
D) 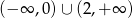
Punkty 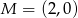 i
i 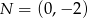 są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
A) 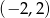 B)
B) 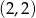 C)
C) 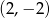 D)
D) 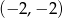
Pole rombu o obwodzie 40 jest równe 35. Kąt ostry tego rombu ma miarę  . Wtedy
. Wtedy
A) 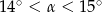 B)
B) 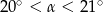 C)
C) 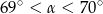 D)
D) 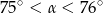
Jeden bok równoległoboku ma długość 120 cm, a drugi ma długość 60 cm. Przekątna tego równoległoboku może mieć długość
A) 50 cm B) 60 cm C) 120 cm D) 200 cm
Współczynnik kierunkowy prostej, na której leżą punkty 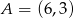 oraz
oraz 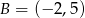 , jest równy
, jest równy
A) 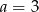 B)
B) 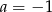 C)
C) 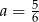 D)
D) 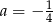
Odcinek 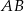 jest średnicą okręgu o środku
jest średnicą okręgu o środku  .
.
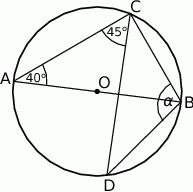
Miara kąta  oznaczonego na rysunku literą
oznaczonego na rysunku literą  jest równa
jest równa
A)  B)
B) 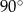 C)
C) 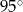 D)
D) 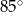
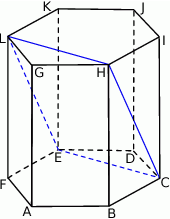
W graniastosłupie prawidłowym sześciokątnym 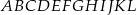 wierzchołki
wierzchołki 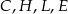 połączono odcinkami (tak jak na rysunku).
połączono odcinkami (tak jak na rysunku).
Wskaż kąt między bokiem 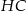 czworokąta
czworokąta 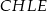 i płaszczyzną podstawy tego graniastosłupa.
i płaszczyzną podstawy tego graniastosłupa.
A) 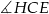 B)
B) 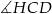 C)
C) 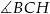 D)
D) 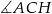
Dany jest trójkąt prostokątny o długościach boków 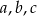 , gdzie
, gdzie 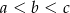 . Obracając ten trójkąt, wokół prostej zawierającej krótszą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej krótszą przyprostokątną o kąt 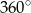 , otrzymujemy bryłę, której objętość jest równa
, otrzymujemy bryłę, której objętość jest równa
A) 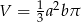 B)
B) 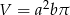 C)
C) 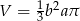 D)
D) 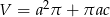
Na planie miasta, narysowanym w skali 1:25 000, park jest prostokątem o bokach 2 cm i 4 cm. Stąd wynika, że ten park ma powierzchnię
A) 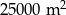 B)
B) 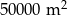 C)
C) 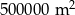 D)
D) 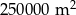
Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 6 i niepodzielnych przez 9?
A) 60 B) 120 C) 100 D) 150
W każdym z trzech pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 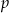 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie jedna z trzech wylosowanych kul będzie czerwona. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie jedna z trzech wylosowanych kul będzie czerwona. Wtedy
A) 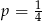 B)
B) 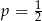 C)
C) 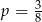 D)
D) 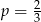
Zadania otwarte
Wyznacz wszystkie liczby dodatnie  spełniające nierówność
spełniające nierówność 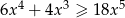 .
.
Rozwiąż równanie 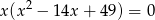 .
.
Kąt  jest ostry i
jest ostry i 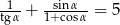 . Oblicz
. Oblicz 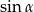 .
.
Wykaż, że równanie 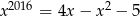 nie ma rozwiązań rzeczywistych.
nie ma rozwiązań rzeczywistych.
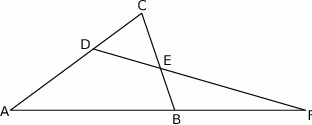
Dany jest trójkąt 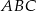 , w którym
, w którym 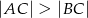 . Na bokach
. Na bokach 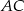 i
i 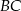 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 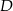 i
i 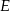 , że
, że 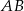 i
i 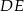 przecinają się w punkcie
przecinają się w punkcie 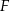 (zobacz rysunek). Wykaż, że jeżeli
(zobacz rysunek). Wykaż, że jeżeli 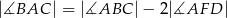 , to
, to 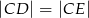 .
.
Wykaż, że dla dowolnych różnych liczb rzeczywistych 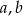 prawdziwa jest nierówność
prawdziwa jest nierówność
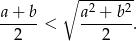
Wśród 93 pracowników pewnego zakładu pracy przeprowadzono badania ankietowe, związane z korzystaniem z dostępnych środków komunikacji miejskiej. W poniższej tabeli przedstawiono informacje o tym, ile osób korzysta z komunikacji tramwajowej, oraz ile osób korzysta z komunikacji autobusowej.
| Rodzaj komunikacji miejskiej | Liczba osób |
| tramwajowa | 43 |
| autobusowa | 47 |
Uwaga! 28 osób spośród ankietowanych korzysta zarówno z komunikacji autobusowej jak i tramwajowej.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba spośród ankietowanych nie korzysta z komunikacji miejskiej. Wynik przedstaw w formie nieskracalnego ułamka.
Punkty 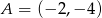 i
i 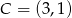 są wierzchołkami rombu
są wierzchołkami rombu 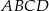 , którego wierzchołek
, którego wierzchołek 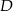 leży na prostej
leży na prostej 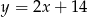 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 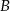 i
i 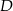 .
.
W ostrosłupie prawidłowym trójkątnym stosunek pola powierzchni bocznej do pola podstawy jest równe 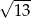 . Oblicz miarę kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy.
. Oblicz miarę kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy.

