/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom podstawowy 10 marca 2014 Czas pracy: 170 minut
Zadania zamknięte
Oprocentowanie kredytu w banku wynosiło 15%. Bank podwyższył oprocentowanie kredytu o 3 punkty procentowe. O ile procent zostało zwiększone oprocentowanie tego kredytu?
A) 20% B) 18% C) 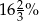 D) 12%
D) 12%
Ile liczb wymiernych znajduje się w zbiorze
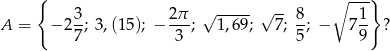
A) 3 B) 4 C) 5 D) 6
Zbiór rozwiązań nierówności 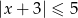 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
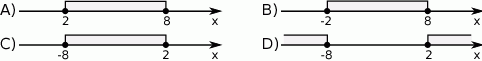
Wielomian 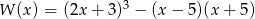 przedstawiony w postaci sumy algebraicznej przyjmuje postać:
przedstawiony w postaci sumy algebraicznej przyjmuje postać:
A) 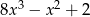 B)
B) 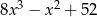 C)
C) 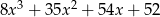 D)
D) 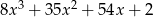
Punkt 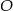 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  przedstawiony na rysunku ma miarę:
przedstawiony na rysunku ma miarę:
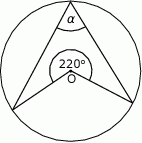
A) 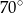 B)
B) 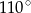 C)
C) 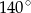 D)
D) 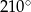
Jeżeli 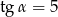 , to wartość wyrażenia
, to wartość wyrażenia 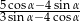 jest równa
jest równa
A) 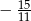 B)
B) 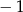 C)
C) 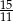 D)
D) 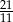
Zdanie „różnica kwadratów dwóch kolejnych liczb naturalnych nieparzystych jest niemniejsza niż 5” przedstawiono w postaci nierówności:
A) 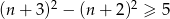
B) 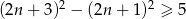
C) 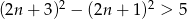
D) ![2 [(2n + 3) − (2n + 1)] ≥ 5](https://img.zadania.info/zes/0066517/HzesT25x.gif)
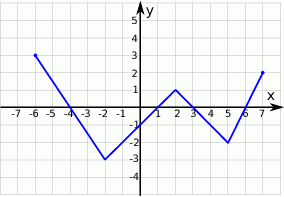
Na rysunku przedstawiony jest wykres pewnej funkcji 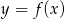 . Przyjmuje ona wartości niedodatnie dla argumentów:
. Przyjmuje ona wartości niedodatnie dla argumentów:
A) 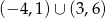 B)
B) 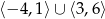 C)
C) 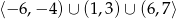 D)
D) 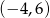
Wyrażenie 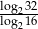 ma wartość równą
ma wartość równą
A) 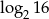 B)
B) 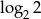 C)
C)  D) 2
D) 2
W ciągu arytmetycznym 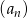 dane są:
dane są: 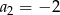 i
i 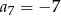 . Wtedy
. Wtedy
A) 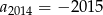 B)
B) 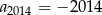 C)
C) 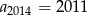 D)
D) 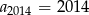
Rozwiązaniem nierówności 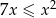 jest zbiór
jest zbiór
A) 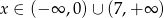 B)
B) 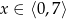 C)
C) 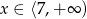 D)
D) 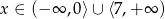
Dla 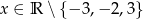 wyrażenie
wyrażenie 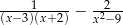 jest równe
jest równe
A) 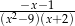 B)
B) 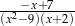 C)
C) 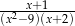 D)
D) 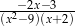
Wartość wyrażenia 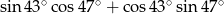 jest równa
jest równa
A) 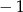 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
Średnia danych przestawionych na wykresie słupkowym jest równa:
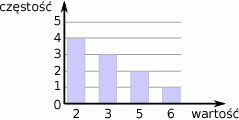
A) 8,25 B) 4 C) 3,3 D) 0,625
Liczba 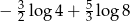 jest równa
jest równa
A) 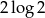 B)
B) 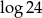 C) 2 D)
C) 2 D) 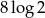
Wielokąt o polu 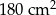 przekształcono przez podobieństwo o skali
przekształcono przez podobieństwo o skali 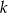 tak, że jego pole zmniejszyło się o
tak, że jego pole zmniejszyło się o 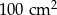 . Skala podobieństwa jest równa:
. Skala podobieństwa jest równa:
A) 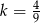 B)
B) 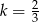 C)
C) 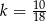 D)
D) 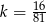
Równanie prostej równoległej do prostej 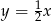 przechodzącej przez punkt
przechodzącej przez punkt 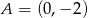 ma postać
ma postać
A) 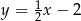 B)
B) 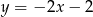 C)
C) 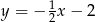 D)
D) 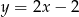
Na rysunku przedstawiono wykres funkcji 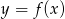 .
.
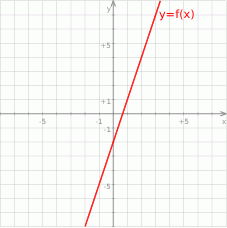
Wzór opisujący funkcję 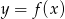 ma postać:
ma postać:
A) 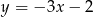 B)
B) 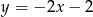 C)
C) 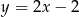 D)
D) 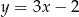
Ciągiem geometrycznym jest ciąg określony wzorem
A) 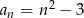 B)
B) 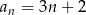 C)
C) 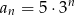 D)
D) 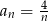
Przekątna sześcianu jest o 3 dłuższa od długości jego krawędzi. Długość krawędzi sześcianu jest równa
A) 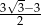 B)
B) 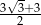 C)
C) 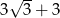 D)
D) 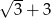
Wielomian 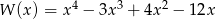 po rozłożeniu na czynniki ma postać:
po rozłożeniu na czynniki ma postać:
A) 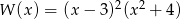
B) 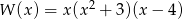
C) 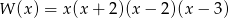
D) 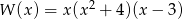
Na rysunku przedstawione są wykresy funkcji 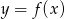 oraz
oraz 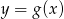 .
.
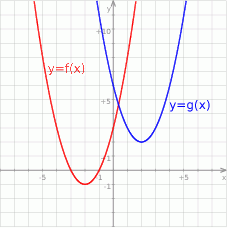
Wówczas :
A) 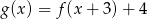
B) 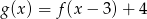
C) 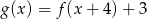
D) 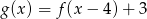
Ze zbioru liczb 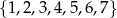 losujemy kolejno dwa razy po jednej cyfrze bez zwracania. Zapisując wylosowane cyfry w kolejności losowania, otrzymujemy liczbę dwucyfrową. Prawdopodobieństwo otrzymania liczby większej od 32 jest równe
losujemy kolejno dwa razy po jednej cyfrze bez zwracania. Zapisując wylosowane cyfry w kolejności losowania, otrzymujemy liczbę dwucyfrową. Prawdopodobieństwo otrzymania liczby większej od 32 jest równe
A) 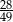 B)
B) 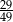 C)
C) 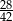 D)
D) 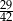
Jeżeli 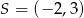 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 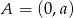 i
i 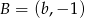 , to
, to
A) 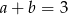 B)
B) 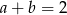 C)
C) 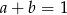 D)
D) 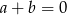
Wykres funkcji 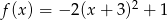 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
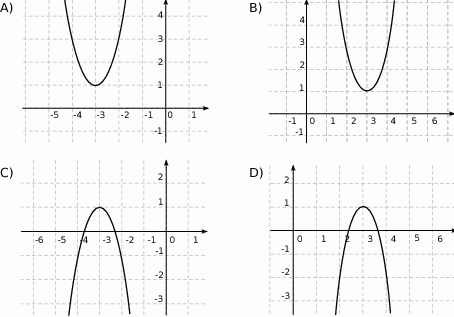
Zadania otwarte
Rozwiąż równanie 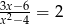 .
.
Uzasadnij, że dwusieczne dwóch sąsiednich kątów równoległoboku przecinają się pod kątem prostym.
Wyznacz najmniejszą i największą wartość funkcji kwadratowej 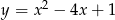 w przedziale
w przedziale 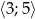 .
.
Ze zbioru liczb trzycyfrowych mniejszych od 500 wybieramy losowo jedną liczbę. Jakie jest prawdopodobieństwo, że będzie to liczba podzielna przez 3 lub przez 5?
Wykaż, że jeżeli 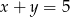 , to
, to 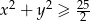 .
.
Przekątne 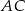 i
i 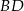 rombu
rombu 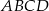 przecinają się w punkcie
przecinają się w punkcie 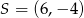 . Wyznacz równanie prostej zawierającej przekątną
. Wyznacz równanie prostej zawierającej przekątną 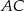 wiedząc, że prosta zawierająca przekątną
wiedząc, że prosta zawierająca przekątną 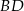 ma równanie
ma równanie 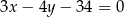 .
.
Objętość graniastosłupa prawidłowego czworokątnego jest równa 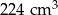 , a promień okręgu opisanego na podstawie ma długość 4 cm. Wyznacz miarę kąta między przekątnymi sąsiednich ścian bocznych wychodzącymi z tego samego wierzchołka graniastosłupa. Wynik podaj z dokładnością do
, a promień okręgu opisanego na podstawie ma długość 4 cm. Wyznacz miarę kąta między przekątnymi sąsiednich ścian bocznych wychodzącymi z tego samego wierzchołka graniastosłupa. Wynik podaj z dokładnością do 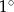 .
.
Samochód przejechał 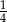 trasy ze średnią prędkością 80 km/h. Na całej trasie średnia prędkość samochodu była równa 64 km/h.Oblicz z jaką średnią prędkością samochód przejechał pozostałą część trasy.
trasy ze średnią prędkością 80 km/h. Na całej trasie średnia prędkość samochodu była równa 64 km/h.Oblicz z jaką średnią prędkością samochód przejechał pozostałą część trasy.
W trójkącie prostokątnym 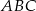 o przeciwprostokątnej
o przeciwprostokątnej 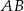 dane są wierzchołki
dane są wierzchołki 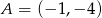 i
i 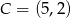 . Punkt
. Punkt 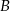 leży na prostej o równaniu
leży na prostej o równaniu 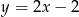 . Wyznacz równanie okręgu opisanego na tym trójkącie.
. Wyznacz równanie okręgu opisanego na tym trójkącie.

