/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 26 marca 2011 Czas pracy: 180 minut

Zadanie 1
(5 pkt)

Rozwiąż nierówność 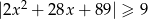2 |2x + 28x + 8 9| ≥ 9 .

Zadanie 2
(5 pkt)

Ciąg 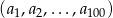(a1,a2,...,a100) jest ciągiem geometrycznym o ilorazie 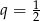q = 1 2 i pierwszym wyrazie równym 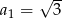√ -- a1 = 3 . Oblicz sumę

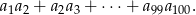
a1a2 + a 2a3 + ⋅⋅ ⋅+ a99a100.

Zadanie 3
(5 pkt)

Wyznacz wszystkie wartości parametru 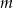m , dla których równanie 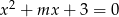2 x + mx + 3 = 0 ma dwa różne pierwiastki rzeczywiste, takie, że suma ich czwartych potęg jest równa 82.

Zadanie 4
(5 pkt)

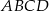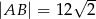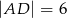Długości boków prostokąta ABCD są równe: √ -- |AB | = 12 2 i |AD | = 6 . Na odcinku 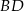BD wybrano punkt 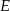E w ten sposób, że 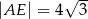√ -- |AE | = 4 3 . Oblicz długość odcinka DE .

Zadanie 5
(6 pkt)

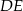Rozwiąż równanie 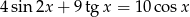4 sin 2x + 9 tgx = 10co sx dla x ∈ ⟨0,2π ⟩ .

Zadanie 6
(5 pkt)

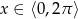Końce cięciwy 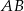AB okręgu o równaniu 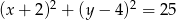(x + 2)2 + (y − 4)2 = 25 leżą na prostej 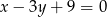x − 3y + 9 = 0 . Oblicz sinus kąta wypukłego 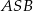ASB , gdzie 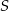S jest środkiem danego okręgu.

Zadanie 7
(4 pkt)

Wykaż, że jeżeli liczby rzeczywiste 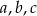a,b,c spełniają równość 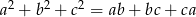2 2 2 a + b + c = ab + bc + ca to a = b = c .

Zadanie 8
(4 pkt)

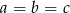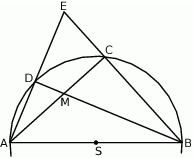
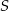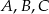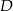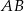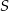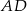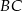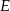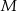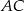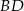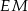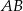Na okręgu o środku S wybrano punkty A ,B,C i D w ten sposób, że prosta AB zawiera punkt S , a proste AD i BC przecinają się w punkcie E . Punkt M jest punktem wspólnym prostych AC i BD . Wykaż, że proste EM i AB są prostopadłe.

PIC

Zadanie 9
(5 pkt)

W ostrosłup prawidłowy czworokątny wpisano kulę o promieniu 2. Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 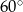60 ∘ . Oblicz objętość tego ostrosłupa.

Zadanie 10
(6 pkt)

Ile jest liczb naturalnych siedmiocyfrowych, których suma cyfr jest równa 4?

Arkusz Wersja PDF
Rozwiązania