/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki poziom rozszerzony 5 maja 2011 Czas pracy: 180 minut
Uzasadnij, że dla każdej liczby całkowitej 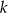 liczba
liczba 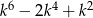 jest podzielna przez 36.
jest podzielna przez 36.
Uzasadnij, że jeżeli 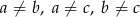 i
i 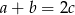 , to
, to 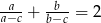 .
.
Wyznacz wszystkie wartości parametru 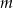 , dla których równanie
, dla których równanie
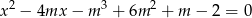
ma dwa różne pierwiastki rzeczywiste 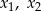 takie, że
takie, że 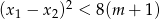 .
.
Rozwiąż równanie 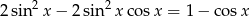 w przedziale
w przedziale 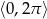 .
.
O ciągu 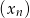 dla
dla 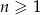 wiadomo, że:
wiadomo, że:
- ciąg
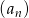 określony wzorem
określony wzorem 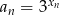 dla
dla 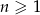 jest geometryczny o ilorazie
jest geometryczny o ilorazie 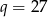 .
. 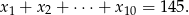
Oblicz 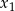 .
.
Podstawa 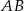 trójkąta równoramiennego
trójkąta równoramiennego 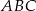 ma długość 8 oraz
ma długość 8 oraz 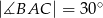 . Oblicz długość środkowej
. Oblicz długość środkowej 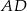 tego trójkąta.
tego trójkąta.
Oblicz miarę kąta między stycznymi do okręgu 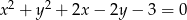 poprowadzonymi przez punkt
poprowadzonymi przez punkt 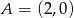 .
.
Wśród wszystkich graniastosłupów prawidłowych sześciokątnych, w których suma długości wszystkich krawędzi jest równa 24, jest taki, który ma największe pole powierzchni bocznej. Oblicz długość krawędzi podstawy tego graniastosłupa.
Oblicz, ile jest liczb ośmiocyfrowych, w zapisie których nie występuje zero, natomiast występują dwie dwójki i występują trzy trójki.
Dany jest czworokąt wypukły 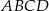 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 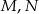 są odpowiednio środkami boków
są odpowiednio środkami boków 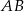 i
i 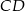 . Punkty
. Punkty 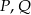 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 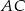 i
i 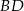 . Uzasadnij, że
. Uzasadnij, że 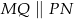 .
.
Dany jest ostrosłup prawidłowy czworokątny 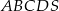 o podstawie
o podstawie 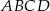 . W trójkącie równoramiennym
. W trójkącie równoramiennym 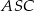 stosunek długości podstawy do długości ramienia jest równy
stosunek długości podstawy do długości ramienia jest równy 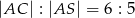 . Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
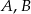 są zdarzeniami losowymi zawartymi w
są zdarzeniami losowymi zawartymi w 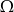 . Wykaż, że jeżeli
. Wykaż, że jeżeli 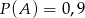 i
i 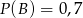 , to
, to 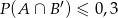 (
(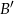 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 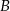 ).
).

