/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki poziom rozszerzony 9 maja 2012 Czas pracy: 180 minut
Wyznacz cztery kolejne liczby całkowite takie, że największa z nich jest równa sumie kwadratów trzech pozostałych liczb.
Rozwiąż nierówność 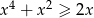 .
.
Rozwiąż równanie 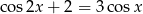 .
.
Oblicz wszystkie wartości parametru 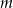 , dla których równanie
, dla których równanie 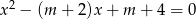 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 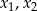 takie, że
takie, że 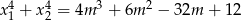 .
.
Trzy liczby tworzą ciąg geometryczny. Jeżeli do drugiej liczby dodamy 8, to ciąg ten zmieni się w arytmetyczny. Jeżeli zaś do ostatniej liczby nowego ciągu arytmetycznego dodamy 64, to tak otrzymany ciąg będzie znów geometryczny. Znajdź te liczby. Uwzględnij wszystkie możliwości.
W układzie współrzędnych rozważmy wszystkie punkty 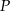 postaci:
postaci: 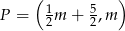 , gdzie
, gdzie 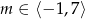 . Oblicz najmniejszą i największą wartość
. Oblicz najmniejszą i największą wartość 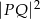 , gdzie
, gdzie 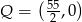 .
.
Udowodnij, że jeżeli 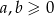 , to prawdziwa jest nierówność
, to prawdziwa jest nierówność 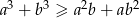 .
.
Oblicz, ile jest liczb naturalnych ośmiocyfrowych takich, że iloczyn cyfr w ich zapisie dziesiętnym jest równy 12.
Dany jest prostokąt 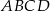 , w którym
, w którym 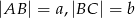 i
i 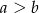 . Odcinek
. Odcinek 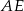 jest wysokością trójkąta
jest wysokością trójkąta 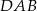 opuszczoną na jego bok
opuszczoną na jego bok 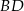 . Wyraź pole trójkąta
. Wyraź pole trójkąta 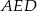 za pomocą
za pomocą  i
i 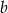 .
.
Podstawą ostrosłupa 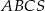 jest trójkąt równoramienny
jest trójkąt równoramienny 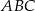 . Krawędź
. Krawędź 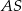 jest wysokością ostrosłupa oraz
jest wysokością ostrosłupa oraz 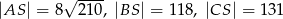 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Zdarzenia losowe 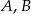 są zawarte w
są zawarte w 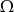 oraz
oraz 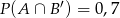 (
(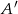 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 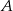 ,
, 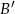 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 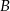 ). Wykaż, że
). Wykaż, że 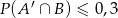 .
.

