/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 2 kwietnia 2016 Czas pracy: 180 minut
Zadania zamknięte
Granica 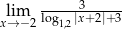
A) jest równa 0 B) jest równa 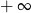 C) jest równa
C) jest równa 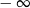 D) nie istnieje
D) nie istnieje
Wyrażenie 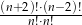 dla liczby naturalnej
dla liczby naturalnej 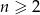 jest równe
jest równe
A)  B)
B) 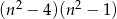 C)
C) 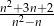 D)
D) 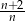
Która z poniższych funkcji, określonych w zbiorze liczb rzeczywistych, nie ma minimum lokalnego ani maksimum lokalnego?
A) 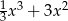 B)
B) 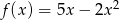 C)
C) 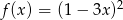 D)
D) 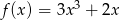
Równanie 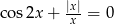 w zbiorze
w zbiorze 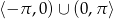
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma więcej niż dwa rozwiązania rzeczywiste.
Liczba pierwiastków całkowitych wielomianu 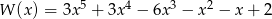 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Zadania otwarte
Wyznacz wszystkie wartości  , dla których trzy liczby:
, dla których trzy liczby: 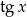 ,
, 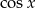 ,
, 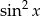 , tworzą ciąg geometryczny (w podanej kolejności).
, tworzą ciąg geometryczny (w podanej kolejności).
Niech 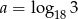 . Wykaż, że
. Wykaż, że 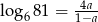 .
.
Wykaż, że jeżeli w trójkącie dwusieczna pokrywa się ze środkową, to trójkąt ten jest równoramienny.
Rozwiąż nierówność 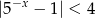 .
.
Wielomian 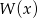 stopnia 3 jest podzielny przez trójmian kwadratowy
stopnia 3 jest podzielny przez trójmian kwadratowy 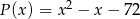 . Wiadomo ponadto, że
. Wiadomo ponadto, że 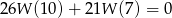 . Wyznacz miejsca zerowe wielomianu
. Wyznacz miejsca zerowe wielomianu 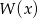 .
.
Ciąg 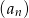 jest określony dla
jest określony dla 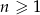 i spełnia warunek
i spełnia warunek
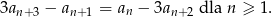
Oblicz sumę dwóch początkowych wyrazów ciągu 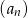 jeżeli suma wszystkich jego wyrazów jest równa 2016.
jeżeli suma wszystkich jego wyrazów jest równa 2016.
Funkcja 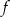 określona jest wzorem
określona jest wzorem 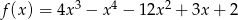 dla
dla 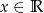 . Wykaż, że
. Wykaż, że
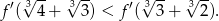
Dany jest czworokąt wypukły 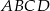 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 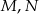 są odpowiednio środkami boków
są odpowiednio środkami boków 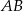 i
i 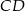 . Punkty
. Punkty 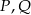 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 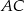 i
i 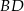 . Uzasadnij, że jeżeli odcinki
. Uzasadnij, że jeżeli odcinki 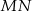 i
i 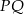 są prostopadłe, to
są prostopadłe, to 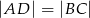 .
.
Z talii 52 kart w czterech kolorach wybieramy losowo 2 karty. Oblicz prawdopodobieństwo, że wybrane karty to król i as, przy założeniu, że wybrane karty mają różne kolory.
Punkty 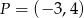 ,
, 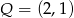 i
i 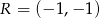 są środkami boków równoległoboku. Wyznacz współrzędne wierzchołków tego równoległoboku.
są środkami boków równoległoboku. Wyznacz współrzędne wierzchołków tego równoległoboku.
Pierwiastki wielomianu 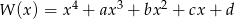 tworzą czterowyrazowy ciąg arytmetyczny o sumie wyrazów równej zero. Wiadomo ponadto, że
tworzą czterowyrazowy ciąg arytmetyczny o sumie wyrazów równej zero. Wiadomo ponadto, że 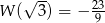 . Oblicz współczynniki
. Oblicz współczynniki 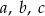 i
i 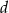 . Rozważ wszystkie możliwe przypadki.
. Rozważ wszystkie możliwe przypadki.
Rozpatrujemy wszystkie stożki, w których suma sześcianów długości promienia podstawy i wysokości jest równa 12. Wyznacz ten spośród rozpatrywanych stożków, którego objętość jest największa. Oblicz tę objętość.

