/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 14 kwietnia 2012 Czas pracy: 170 minut
Zadania zamknięte
Pierwsza rata, która stanowi 9% ceny kanapy, jest o 84 zł niższa od drugiej raty, która stanowi 12% ceny kanapy. Kanapa kosztuje
A) 280 zł B) 2788 zł C) 2520 zł D) 2800 zł
Przedział 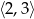 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 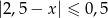 B)
B) 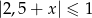 C)
C) 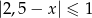 D)
D) 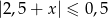
Kąt  jest kątem ostrym i
jest kątem ostrym i 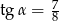 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 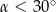 B)
B) 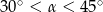 C)
C) 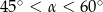 D)
D) 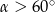
Różnica 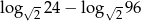 jest równa
jest równa
A) 4 B) 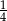 C)
C) 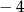 D)
D) 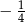
Jeżeli 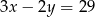 i
i 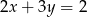 to
to
A) 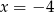 B)
B) 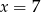 C)
C) 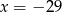 D)
D) 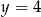
Punkt 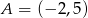 leży na prostej
leży na prostej 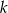 prostopadłej do prostej o równaniu
prostopadłej do prostej o równaniu 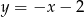 . Prosta
. Prosta 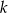 ma równanie
ma równanie
A) 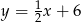 B)
B) 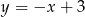 C)
C) 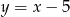 D)
D) 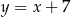
Wskaż, który zbiór przedstawiony na osi liczbowej jest zbiorem liczb spełniających jednocześnie następujące nierówności: 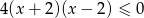 i
i 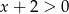 .
.
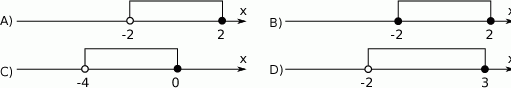
Wartość wyrażenia 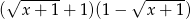 dla
dla 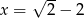 jest równa
jest równa
A) 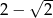 B)
B) 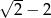 C)
C) 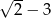 D)
D) 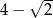
Zbiorem wartości funkcji kwadratowej 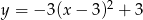 jest
jest
A) 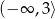 B)
B) 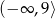 C)
C) 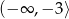 D)
D) 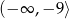
Funkcja liniowa określona jest wzorem 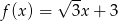 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 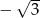 B)
B) 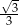 C)
C) 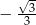 D)
D) 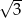
Na rysunku przedstawiony jest wykres funkcji 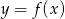 .
.
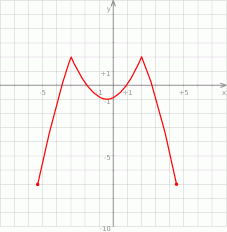
Które z równań ma dokładnie trzy rozwiązania?
A) 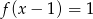 B)
B) 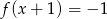 C)
C) 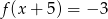 D)
D) 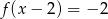
W ciągu arytmetycznym 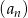 dane są:
dane są: 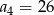 i
i 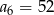 . Wtedy wyraz
. Wtedy wyraz 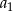 jest równy
jest równy
A) 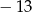 B) 0 C) 13 D)
B) 0 C) 13 D) 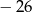
W ciągu geometrycznym 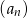 dane są:
dane są: 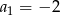 i
i 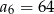 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 2 B) 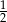 C)
C) 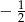 D)
D) 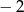
Dane są punkty 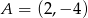 oraz
oraz 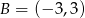 . Odcinek
. Odcinek 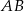 ma długość
ma długość
A) 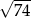 B)
B) 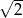 C)
C) 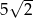 D)
D) 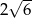
Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 7. Wysokość opuszczona na podstawę ma długość
A) 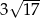 B)
B) 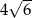 C)
C) 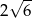 D)
D) 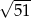
Objętość stożka o wysokości 4 i średnicy podstawy 6 jest równa
A) 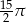 B)
B) 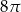 C)
C) 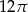 D)
D) 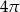
Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 15 jest równe
A) 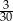 B)
B) 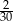 C)
C) 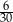 D)
D) 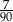
Pole rombu o kącie ostrym 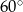 jest równe
jest równe 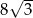 . Bok tego rombu ma długość
. Bok tego rombu ma długość
A) 6 B) 2 C) 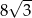 D) 4
D) 4
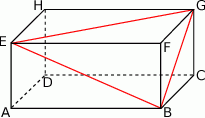
W prostopadłościanie 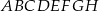 mamy:
mamy: 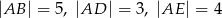 . Który z odcinków
. Który z odcinków 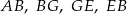 jest najdłuższy?
jest najdłuższy?
A) 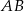 B)
B) 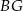 C)
C) 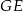 D)
D) 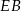
Grupa przypadkowych przechodniów została poproszona o odpowiedź na pytanie: „ile osób liczy Państwa rodzina?”. Wyniki przedstawiono w tabeli:
| Liczba osób w rodzinie | Liczba odpowiedzi |
| 2 | 6 |
| x | 12 |
| 5 | 2 |
Średnia liczba osób w rodzinie dla pytanych osób jest równa 3,5. Wtedy liczba  jest równa
jest równa
A) 3 B) 4 C) 1 D) 7
Zadania otwarte
Rozwiąż równanie 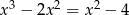 .
.
Uzasadnij, że jeżeli 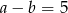 i
i 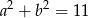 , to
, to 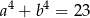 .
.
Kąt  jest ostry i
jest ostry i 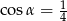 . Oblicz
. Oblicz 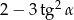 .
.
Wyznacz równania stycznych do okręgu o równaniu 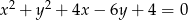 , równoległych do osi rzędnych układu współrzędnych.
, równoległych do osi rzędnych układu współrzędnych.
Przez wierzchołek 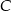 prostokąta
prostokąta 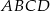 poprowadzono prostą, która przecięła proste
poprowadzono prostą, która przecięła proste 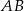 i
i 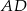 w punktach
w punktach 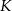 i
i 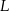 odpowiednio. Wykaż, że
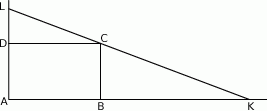
odpowiednio. Wykaż, że 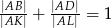 .
.
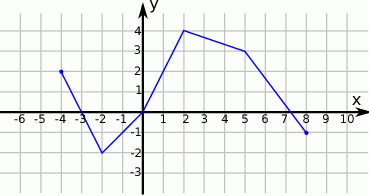
Na rysunku przedstawiono wykres funkcji 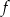 .
.
Odczytaj z wykresu i zapisz:
- maksymalne przedziały monotoniczności funkcji
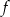 ,
, - liczbę rozwiązań równania
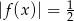 .
.
Wyznacz sumę wszystkich liczb dwucyfrowych, które są podzielne przez 4.
W równoległoboku, który nie jest prostokątem, krótsza przekątna dzieli go na dwa równoramienne trójkąty prostokątne. Krótszy bok równoległoboku ma długość 8. Oblicz pole tego równoległoboku.
Długość boku rombu jest równa  , a długości jego przekątnych są równe
, a długości jego przekątnych są równe 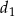 i
i 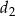 . Oblicz miarę kąta ostrego rombu jeżeli wiadomo, że
. Oblicz miarę kąta ostrego rombu jeżeli wiadomo, że 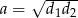 .
.
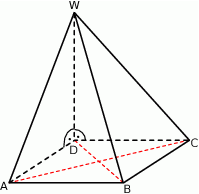
Podstawą ostrosłupa 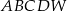 jest kwadrat
jest kwadrat 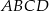 o polu 2. Krawędź boczna
o polu 2. Krawędź boczna 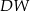 jest wysokością tego ostrosłupa. Długości krawędzi bocznych
jest wysokością tego ostrosłupa. Długości krawędzi bocznych 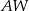 i
i 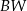 spełniają warunek
spełniają warunek 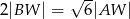 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Samochód przebył w pewnym czasie 210 km. Gdyby jechał o pół godziny krócej to średnia prędkość z jaką przejechał tę trasę byłaby większa o 10 km/h. Oblicz, z jaką średnią prędkością jechał ten samochód.

