/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki poziom rozszerzony
(formuła 2015) 15 maja 2024 Czas pracy: 180 minut
Zadania zamknięte
Odległość punktu 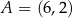 od prostej o równaniu
od prostej o równaniu 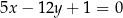 jest równa
jest równa
A) 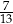 B)
B) 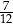 C)
C) 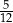 D)
D) 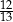
Równanie 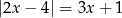 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązań.
B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania.
D) ma dokładnie cztery rozwiązania.
Funkcja 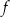 jest określona wzorem
jest określona wzorem 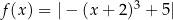 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Zbiorem wartości funkcji
. Zbiorem wartości funkcji 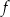 jest przedział
jest przedział
A) 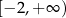 B)
B) 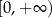 C)
C) 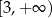 D)
D) 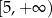
Granica
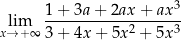
jest równa 3. Wtedy
A) 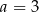 B)
B) 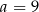 C)
C) 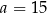 D)
D) 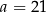
Zadania otwarte
Wielomian 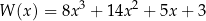 jest iloczynem wielomianów
jest iloczynem wielomianów 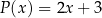 oraz
oraz 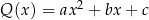 . Oblicz wartości współczynników:
. Oblicz wartości współczynników: 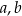 oraz
oraz  .
.
Wykaż, że jeżeli 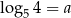 oraz
oraz 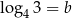 , to
, to 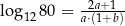 .
.
Dany jest czworokąt wypukły 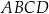 . Przekątne
. Przekątne 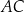 oraz
oraz 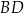 tego czworokąta przecinają się w punkcie
tego czworokąta przecinają się w punkcie 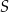 . Wykaż, że jeżeli
. Wykaż, że jeżeli 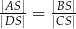 , to na czworokącie
, to na czworokącie 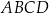 można opisać okrąg.
można opisać okrąg.
Rozważamy wszystkie liczby naturalne, w których zapisie dziesiętnym nie powtarza się jakakolwiek cyfra oraz dokładnie trzy cyfry są nieparzyste i dokładnie dwie cyfry są parzyste. Oblicz, ile jest wszystkich takich liczb.
Funkcja 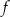 jest określona wzorem
jest określona wzorem
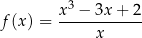
dla każdej liczby rzeczywistej  różnej od zera. W kartezjańskim układzie współrzędnych
różnej od zera. W kartezjańskim układzie współrzędnych 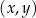 punkt
punkt 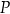 , o pierwszej współrzędnej równej 2, należy do wykresu funkcji
, o pierwszej współrzędnej równej 2, należy do wykresu funkcji 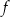 . Prosta o równaniu
. Prosta o równaniu 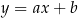 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 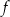 w punkcie
w punkcie 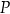 . Oblicz współczynniki
. Oblicz współczynniki  oraz
oraz 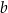 w równaniu tej stycznej.
w równaniu tej stycznej.
Spośród wszystkich liczb naturalnych sześciocyfrowych, których wszystkie cyfry należą do zbioru 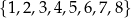 , losujemy jedną. Wylosowanie każdej z tych liczb jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę, która ma następującą własność: kolejne cyfry tej liczby (licząc od lewej strony) tworzą – w podanej kolejności – sześciowyrazowy ciąg malejący.
, losujemy jedną. Wylosowanie każdej z tych liczb jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę, która ma następującą własność: kolejne cyfry tej liczby (licząc od lewej strony) tworzą – w podanej kolejności – sześciowyrazowy ciąg malejący.
Trzywyrazowy ciąg 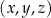 jest geometryczny i rosnący. Suma wyrazów tego ciągu jest równa 105. Liczby
jest geometryczny i rosnący. Suma wyrazów tego ciągu jest równa 105. Liczby 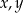 oraz
oraz  są – odpowiednio – pierwszym, drugim oraz szóstym wyrazem ciągu arytmetycznego
są – odpowiednio – pierwszym, drugim oraz szóstym wyrazem ciągu arytmetycznego 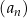 , określonego dla każdej liczby naturalnej
, określonego dla każdej liczby naturalnej 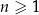 . Oblicz
. Oblicz 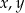 oraz
oraz  .
.
Rozwiąż równanie 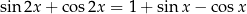 w przedziale
w przedziale ![[0,2π ]](https://img.zadania.info/zes/0068137/HzesT54x.png) .
.
Promień okręgu opisanego na trójkącie 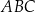 jest równy 17. Najdłuższym bokiem tego trójkąta jest bok
jest równy 17. Najdłuższym bokiem tego trójkąta jest bok 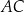 , a długości dwóch pozostałych boków są równe
, a długości dwóch pozostałych boków są równe 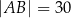 oraz
oraz 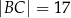 . Oblicz miarę kąta
. Oblicz miarę kąta 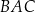 oraz długość boku
oraz długość boku 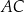 tego trójkąta.
tego trójkąta.
W kartezjańskim układzie współrzędnych 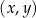 środek
środek 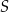 okręgu o promieniu
okręgu o promieniu 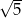 leży na prostej o równaniu
leży na prostej o równaniu 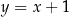 . Przez punkt
. Przez punkt 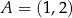 , którego odległość od punktu
, którego odległość od punktu 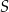 jest większa od
jest większa od 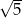 , poprowadzono dwie proste styczne do tego okręgu w punktach – odpowiednio –
, poprowadzono dwie proste styczne do tego okręgu w punktach – odpowiednio – 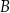 i
i 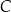 . Pole czworokąta
. Pole czworokąta 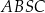 jest równe 15. Oblicz współrzędne punktu
jest równe 15. Oblicz współrzędne punktu 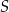 . Rozważ wszystkie przypadki.
. Rozważ wszystkie przypadki.
Wyznacz wszystkie wartości parametru 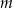 , dla których równanie
, dla których równanie
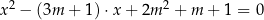
ma dwa różne rozwiązania rzeczywiste 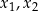 spełniające warunek
spełniające warunek
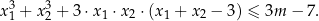
Rozważamy wszystkie graniastosłupy prawidłowe trójkątne o objętości 3456, których krawędź podstawy ma długość nie większą niż 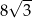 .
.
-
Wykaż, że pole
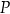 powierzchni całkowitej graniastosłupa w zależności od długości
powierzchni całkowitej graniastosłupa w zależności od długości  krawędzi podstawy graniastosłupa jest określone wzorem
krawędzi podstawy graniastosłupa jest określone wzorem 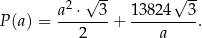
-
Wyznacz długość krawędzi podstawy tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.

