/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Matura 2010
poziom podstawowy Informator CKE, zestaw 1 Czas pracy: 170 minut
Zadania zamknięte
Punkty 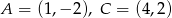 są dwoma wierzchołkami trójkąta równobocznego
są dwoma wierzchołkami trójkąta równobocznego 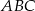 . Wysokość tego trójkąta jest równa
. Wysokość tego trójkąta jest równa
A) 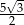 B)
B) 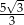 C)
C) 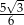 D)
D) 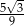
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej.
![]()
A) 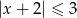 B)
B) 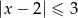 C)
C) 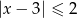 D)
D) 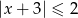
Drut o długości 27 m pocięto na trzy części, których stosunek długości jest równy 2:3:4. Jaką długość ma najkrótsza z tych części?
A) 4,5 m B) 6 m C) 6,75 m D) 9 m
Ile punktów wspólnych ma prosta o równaniu 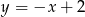 z okręgiem o środku w początku układu współrzędnych i promieniu 2?
z okręgiem o środku w początku układu współrzędnych i promieniu 2?
A) 0 B) 1 C) 2 D) 3
Liczby: 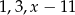 , w podanej kolejności, są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Liczba
, w podanej kolejności, są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Liczba  jest równa
jest równa
A) 5 B) 9 C) 16 D) 20
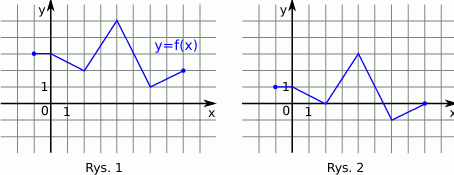
Na rysunku 1 jest przedstawiony wykres funkcji 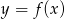 .
.
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 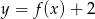 B)
B) 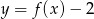 C)
C) 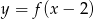 D)
D) 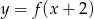
Kąt  jest ostry i
jest ostry i 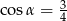 . Wtedy
. Wtedy 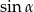 jest równy
jest równy
A) 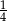 B)
B) 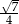 C)
C) 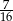 D)
D) 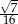
Wskaż funkcję kwadratową, której zbiorem wartości jest przedział 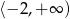 .
.
A) 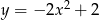 B)
B) 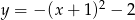 C)
C) 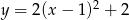 D)
D) 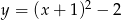
Liczba 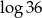 jest równa
jest równa
A) 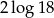 B)
B) 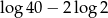 C)
C) 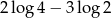 D)
D) 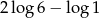
Ile jest wszystkich liczb naturalnych dwucyfrowych, w których obie cyfry są parzyste?
A) 16 B) 20 C) 24 D) 25
Powierzchnia boczna stożka po rozwinięciu jest półkolem o promieniu 12 cm. Podstawa tego stożka jest kołem o promieniu
A) 12 cm B) 6 cm C) 3 cm D) 1 cm
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
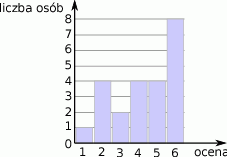
Mediana ocen uzyskanych przez uczniów jest równa
A) 6 B) 5 C) 4,5 D) 4
Prosta 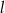 ma równanie
ma równanie 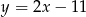 . Wskaż równanie prostej równoległej do
. Wskaż równanie prostej równoległej do 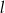 .
.
A) 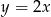 B)
B) 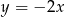 C)
C) 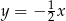 D)
D) 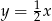
Liczba rozwiązań równania 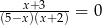 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Wskaż przedział, który jest zbiorem rozwiązań nierówności 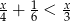 .
.
A) 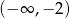 B)
B) 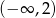 C)
C) 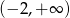 D)
D) 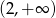
Przekątna prostopadłościanu o wymiarach 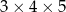 ma długość
ma długość
A) 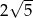 B)
B) 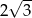 C)
C) 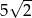 D)
D) 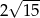
Liczba 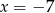 jest miejscem zerowym funkcji liniowej
jest miejscem zerowym funkcji liniowej 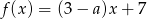 dla
dla
A) 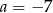 B)
B) 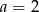 C)
C) 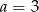 D)
D) 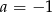
Zbiorem rozwiązań nierówności 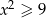 jest
jest
A) 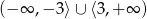 B)
B) 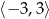 C)
C) 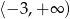 D)
D) 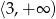
Zaznaczony na rysunku kąt  jest równy
jest równy
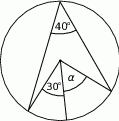
A) 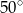 B)
B) 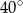 C)
C) 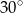 D)
D) 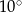
Która z liczb jest rozwiązaniem równania 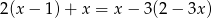 ?
?
A) 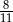 B)
B) 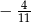 C)
C)  D) -1
D) -1
Liczba 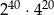 jest równa
jest równa
A) 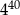 B)
B) 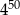 C)
C) 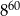 D)
D) 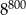
Wskaż liczbę, której 4% jest równe 8.
A) 3,2 B) 32 C) 100 D) 200
Kąt  jest ostry i
jest ostry i 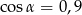 . Wówczas
. Wówczas
A) 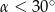 B)
B) 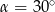 C)
C) 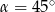 D)
D) 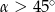
Trzeci wyraz ciągu geometrycznego jest równy 4, a czwarty wyraz tego ciągu jest równy -2. Pierwszy wyraz tego ciągu jest równy
A) 16 B) -16 C) 8 D) -8
Ze zbioru liczb 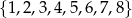 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 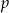 jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
A) 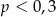 B)
B) 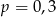 C)
C) 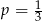 D)
D) 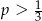
Zadania otwarte
Dany jest ciąg 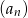 określony wzorem
określony wzorem 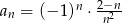 dla
dla 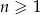 . Oblicz
. Oblicz 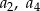 i
i 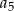 .
.
Rozwiąż równanie 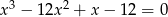 .
.
Punkt 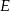 leży na ramieniu
leży na ramieniu 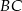 trapezu
trapezu 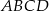 , w którym
, w którym 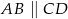 . Udowodnij, że
. Udowodnij, że 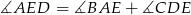 .
.
Podaj przykład liczb całkowitych dodatnich, spełniających nierówność 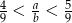 .
.
Dany jest prostokąt o bokach  i
i 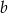 oraz prostokąt o bokach
oraz prostokąt o bokach  i
i 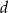 . Długość boku
. Długość boku  to 90% długości boku
to 90% długości boku  . Długość boku
. Długość boku 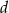 to 120% długości boku
to 120% długości boku 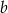 . Oblicz, ile procent pola prostokąta o bokach
. Oblicz, ile procent pola prostokąta o bokach  i
i 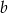 stanowi pole prostokąta o bokach
stanowi pole prostokąta o bokach  i
i 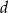 .
.
Dwa pociągi towarowe wyjechały z miast 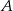 i
i 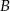 oddalonych od siebie o 540 km. Pociąg jadący z miasta
oddalonych od siebie o 540 km. Pociąg jadący z miasta 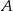 do miasta
do miasta 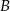 wyjechał o godzinę wcześniej niż pociąg jadący z miasta
wyjechał o godzinę wcześniej niż pociąg jadący z miasta 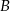 do miasta
do miasta 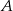 i jechał z prędkością o 9 km/h mniejszą. Pociągi te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te pociągi.
i jechał z prędkością o 9 km/h mniejszą. Pociągi te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te pociągi.
Dane są dwa pojemniki. W pierwszym z nich znajduje się 9 kul: 4 białe, 3 czarne i 2 zielone. W drugim pojemniku jest 6 kul: 2 białe , 3 czarne i 1 zielona. Z każdego pojemnika losujemy po jednej kuli. Oblicz prawdopodobieństwo wylosowania dwóch kul tego samego koloru.
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 8. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 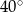 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.

