/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 6 kwietnia 2024 Czas pracy: 180 minut
Liczba 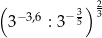 jest równa
jest równa
A) 0,9 B) 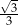 C)
C) 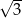 D)
D) 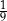
Liczba 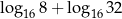 jest równa
jest równa
A) 256 B) 64 C) 4 D) 2
Dana jest nierówność
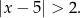
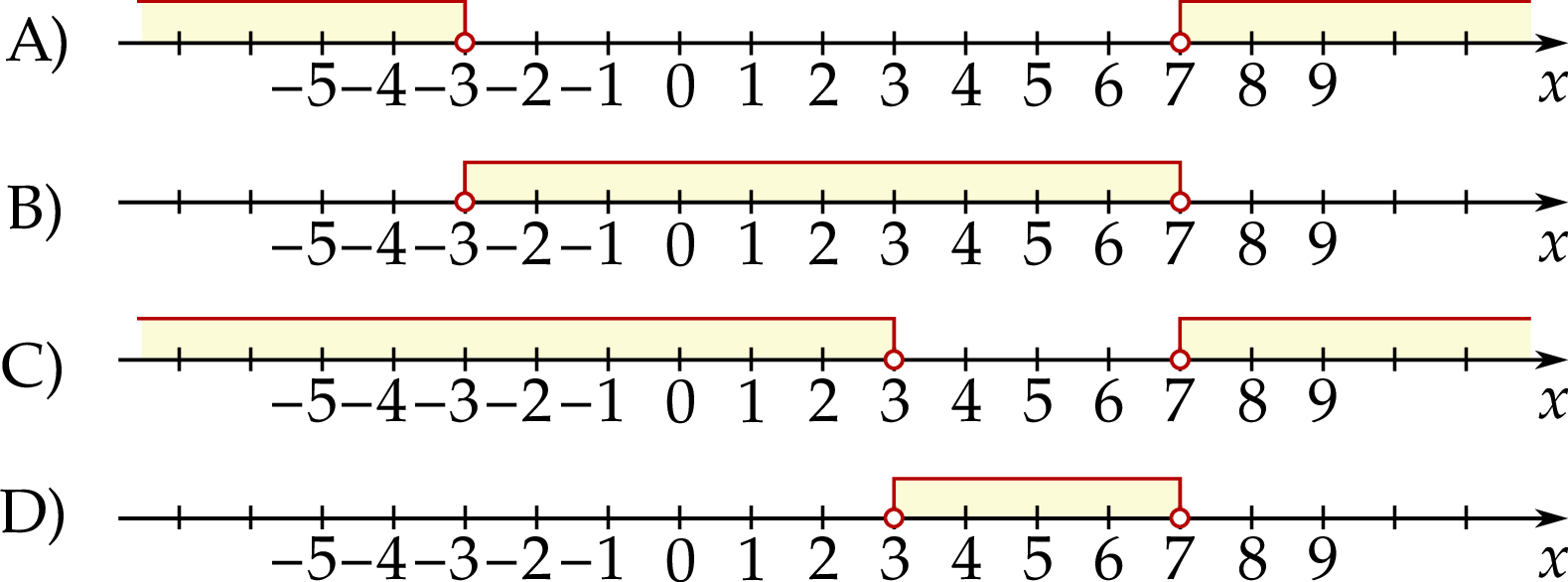
Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających powyższą nierówność?
Klient wpłacił do banku 40 000 zł na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości 6% od kwoty bieżącego kapitału znajdującego się na lokacie. Po dwóch latach oszczędzania łączna wartość doliczonych odsetek na tej lokacie (bez uwzględniania podatków) jest równa
A) 4944 zł B) 4800 zł C) 5088 zł D) 4400 zł
Dany jest prostokąt o bokach długości  i
i 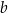 , gdzie
, gdzie 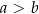 . Obwód tego prostokąta jest równy 40. Jeden z boków prostokąta jest o 4 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Obwód tego prostokąta jest równy 40. Jeden z boków prostokąta jest o 4 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Zależności między długościami boków tego prostokąta zapisano w układzie równań
A) 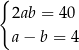 B)
B) 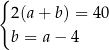 C)
C) 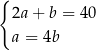
D) 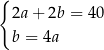 E)
E) 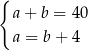 F)
F) 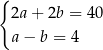
Informacja do zadań 6.1 i 6.2
Masa 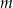 leku
leku 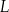 zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
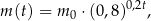
gdzie:
-
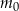 – masa (wyrażona w mg) przyjętej w chwili
– masa (wyrażona w mg) przyjętej w chwili 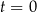 dawki leku,
dawki leku, -
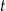 – czas (wyrażony w godzinach) liczony od momentu
– czas (wyrażony w godzinach) liczony od momentu 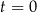 zażycia leku.
zażycia leku.
Chory przyjął jednorazowo lek 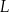 w dawce 300 mg. Oblicz, ile mg leku
w dawce 300 mg. Oblicz, ile mg leku 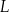 pozostanie w organizmie chorego po 15 godzinach od momentu przyjęcia dawki.
pozostanie w organizmie chorego po 15 godzinach od momentu przyjęcia dawki.
Liczby 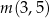 ,
, 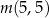 ,
, 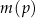 w podanej kolejności tworzą ciąg geometryczny. Liczba
w podanej kolejności tworzą ciąg geometryczny. Liczba 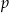 jest równa
jest równa
A) 8,5 B) 9 C) 6 D) 7,5
Jednym z rozwiązań równania 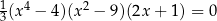 jest liczba
jest liczba
A) 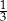 B)
B) 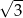 C)
C) 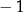 D)
D) 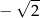
Liczba  jest liczbą całkowitą parzystą, która nie dzieli się przez 4. Wykaż, że liczba
jest liczbą całkowitą parzystą, która nie dzieli się przez 4. Wykaż, że liczba 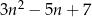 nie jest podzielna przez 4.
nie jest podzielna przez 4.
Podstawa 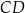 trapezu
trapezu 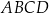 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 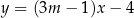 . Wierzchołki
. Wierzchołki 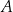 i
i 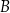 tego trapezu mają odpowiednio współrzędne
tego trapezu mają odpowiednio współrzędne 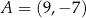 i
i 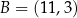 . Liczba
. Liczba 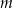 jest zatem równa
jest zatem równa
A) 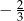 B) 2 C)
B) 2 C) 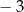 D)
D) 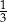
Liczba 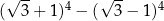 jest równa
jest równa
A) 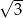 B)
B) 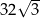 C)
C) 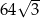 D) 2
D) 2
Rozwiąż równanie
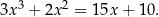
Ciąg arytmetyczny 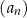 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 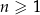 . W tym ciągu
. W tym ciągu 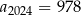 oraz
oraz 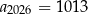 . Wyraz
. Wyraz 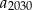 tego ciągu jest równy
tego ciągu jest równy
A) 1100,5 B) 1083 C) 1048 D) 1118
Prosta 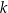 przechodzi przez punkty
przechodzi przez punkty 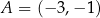 i
i 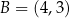 , a prosta
, a prosta 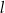 opisana jest równaniem
opisana jest równaniem 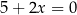 . Tangens kąta ostrego pod jakim przecinają się proste
. Tangens kąta ostrego pod jakim przecinają się proste 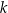 i
i 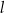 jest równy
jest równy
A) 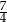 B)
B) 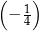 C)
C) 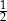 D)
D) 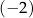
Ciąg 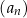 jest określony wzorem
jest określony wzorem
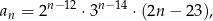
dla każdej liczby naturalnej 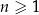 . Który wyraz ciągu
. Który wyraz ciągu 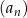 jest równy 466 560?
jest równy 466 560?
A) 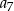 B)
B) 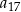 C)
C) 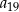 D)
D) 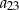
Kąt  jest ostry oraz
jest ostry oraz 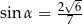 . Tangens kąta
. Tangens kąta  jest równy
jest równy
A) 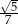 B)
B) 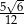 C)
C) 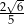 D)
D) 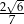
Podstawą trójkąta równoramiennego 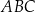 jest odcinek o końcach w punktach
jest odcinek o końcach w punktach 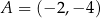 oraz
oraz 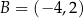 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 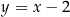 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 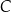 .
.
W trójkącie równoramiennym 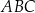 długość podstawy
długość podstawy 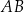 jest równa 4, a długość ramienia
jest równa 4, a długość ramienia 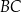 jest równa 6. Dwusieczna kąta
jest równa 6. Dwusieczna kąta 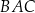 przecina bok
przecina bok 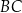 w punkcie
w punkcie 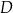 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 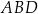 jest prostokątny. jest prostokątny. | P | F |
Odcinek 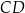 jest krótszy od odcinka jest krótszy od odcinka 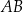 . . | P | F |
Dany jest ciąg geometryczny 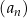 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 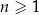 . Pierwszy wyraz tego ciągu jest równy 96, natomiast iloraz ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy 96, natomiast iloraz ciągu jest równy 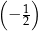 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wyraz 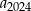 jest liczbą ujemną. jest liczbą ujemną. | P | F |
Różnica  jest równa 96. jest równa 96. | P | F |
Dla każdego kąta ostrego  wyrażenie
wyrażenie 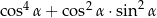 jest równe
jest równe
A) 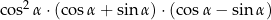 B)
B) 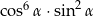
C) 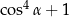 D)
D) 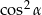
Punkty 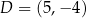 i
i 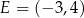 są wierzchołkami sześciokąta foremnego
są wierzchołkami sześciokąta foremnego 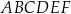 . Pole tego sześciokąta jest równe
. Pole tego sześciokąta jest równe
A) 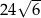 B)
B) 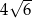 C)
C) 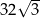 D)
D) 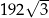
Przekątne trapezu 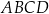 są prostopadłe i przecinają się w punkcie
są prostopadłe i przecinają się w punkcie 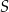 . Podstawa
. Podstawa 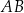 tego trapezu ma długość 15, a odcinki
tego trapezu ma długość 15, a odcinki 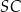 i
i 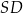 mają odpowiednio długości 6 i 8. Oblicz pole trójkąta
mają odpowiednio długości 6 i 8. Oblicz pole trójkąta 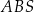 .
.
Odcinek 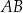 jest średnicą okręgu o środku
jest średnicą okręgu o środku 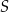 . Prosta
. Prosta 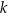 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 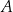 . Prosta
. Prosta 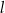 przecina ten okrąg w punktach
przecina ten okrąg w punktach 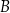 i
i 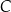 . Proste
. Proste 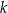 i
i 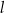 przecinają się w punkcie
przecinają się w punkcie 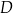 , przy czym
, przy czym 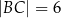 i
i 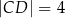 (zobacz rysunek).
(zobacz rysunek).

Odległość punktu 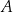 od prostej
od prostej 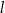 jest równa
jest równa
A) 8 B) 5 C) 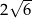 D)
D) 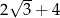
Dany jest prostopadłościan 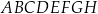 o krawędziach długości
o krawędziach długości 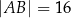 ,
, 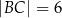 i
i 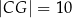 . Wewnątrz tego prostopadłościanu znajduje się punkt
. Wewnątrz tego prostopadłościanu znajduje się punkt 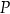 (zobacz rysunek).
(zobacz rysunek).
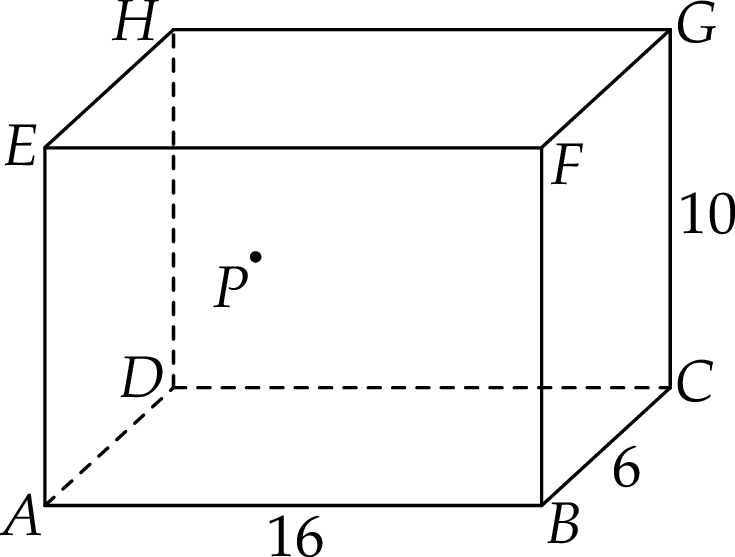
Suma odległości punktu 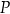 od wszystkich ścian prostopadłościanu
od wszystkich ścian prostopadłościanu 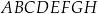 jest równa
jest równa
A) 45 B) 20 C) 25 D) 32
W kartezjańskim układzie współrzędnych 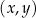 dane są punkty
dane są punkty 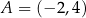 oraz
oraz 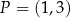 . Punkt
. Punkt 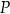 dzieli odcinek
dzieli odcinek 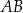 tak, że
tak, że 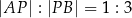 . Punkt
. Punkt 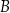 ma współrzędne
ma współrzędne
A) 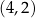 B)
B) 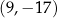 C)
C) 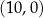 D)
D) 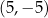
W pewnym ostrosłupie prawidłowym stosunek liczby 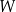 wszystkich wierzchołków do liczby
wszystkich wierzchołków do liczby 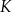 wszystkich krawędzi jest równy
wszystkich krawędzi jest równy 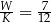 . Podstawą tego ostrosłupa jest
. Podstawą tego ostrosłupa jest
A) kwadrat. B) pięciokąt foremny.
C) sześciokąt foremny. D) siedmiokąt foremny.
Informacja do zadań 26.1 i 26.2
W hurtowni owoców wyselekcjonowane jabłko spełnia normę jakości, gdy jego masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [19 dag, 21 dag]. Pobrano próbę kontrolną liczącą 50 jabłek i następnie zważono każde z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy jabłek w badanej próbie. Na osi poziomej podano – wyrażoną w dekagramach – masę jabłka (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę jabłek o określonej masie.
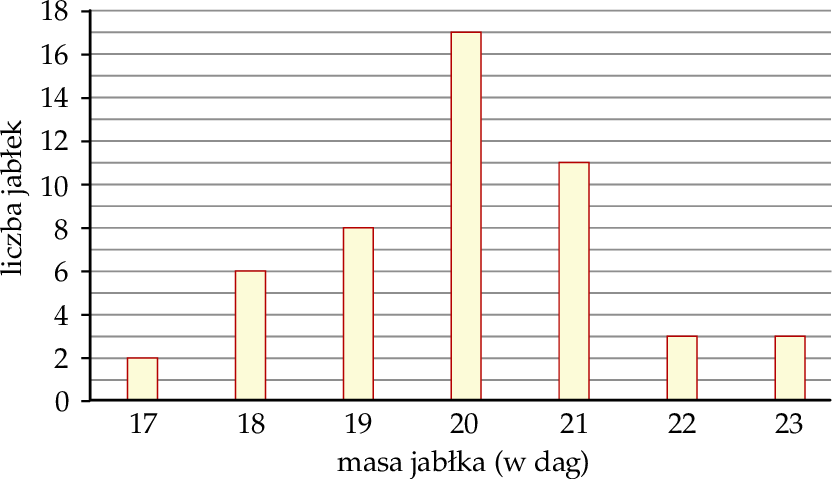
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dominanta masy tych jabłek z danej próby, które nie spełniają normy jakości, jest większa od 20 dag. | P | F |
| Mediana masy 50 zważonych jabłek jest równa 20 dag. | P | F |
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1, 2 albo 3.
Średnia masy 50 zważonych jabłek z pobranej próby kontrolnej jest
| A) mniejsza niż 21 dag, | B) większa niż 21 dag, |
ponieważ
| 1) | większość jabłek waży 20 dag. |
| 2) | suma iloczynów masy i liczby jabłek o takiej masie jest mniejsza niż 1050 dag. |
| 3) | większość jabłek waży co najmniej 20 dag. |
Wszystkich liczb naturalnych trzycyfrowych o sumie cyfr równej 4 jest
A) 9 B) 8 C) 10 D) 11
Cięciwy 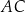 i
i 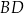 okręgu przecinają się w punkcie
okręgu przecinają się w punkcie 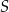 w ten sposób, że
w ten sposób, że 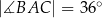 i
i 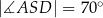 (zobacz rysunek).
(zobacz rysunek).

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 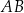 i i 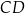 są równoległe. są równoległe. | P | F |
Trójkąty 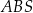 i i 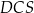 są podobne. są podobne. | P | F |
Informacja do zadań 29.1 i 29.2
Właściciel pewnej pączkarni przeanalizował dane dotyczące liczby obsługiwanych klientów z 40 kolejnych dni. Przyjmijmy, że liczbę 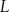 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
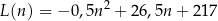
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 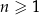 i
i 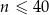 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W jednym z dni poddanych analizie, liczba klientów obsłużonych w pączkarni była równa 448. | P | F |
| W 19 dniu analizowanego okresu obsłużono tyle samo klientów, ile obsłużono w dniu 34. | P | F |
Oblicz jaka była największa liczba klientów pączkarni obsłużonych jednego dnia w okresie poddanym analizie.
Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 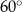 i ma długość równą 6 (zobacz rysunek).
i ma długość równą 6 (zobacz rysunek).
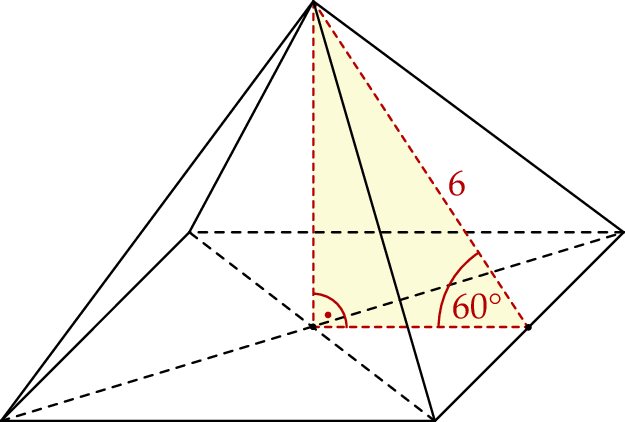
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Funkcja kwadratowa 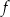 jest określona wzorem
jest określona wzorem 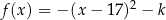 dla pewnej liczby rzeczywistej
dla pewnej liczby rzeczywistej 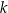 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 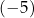 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Drugim miejscem zerowym funkcji 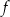 jest liczba 37. jest liczba 37. | P | F |
Największa wartość funkcji 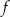 jest równa 484. jest równa 484. | P | F |
Miejscem zerowym funkcji liniowej 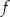 jest liczba
jest liczba 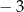 . Wykres tej funkcji przechodzi przez punkt
. Wykres tej funkcji przechodzi przez punkt 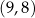 . Wzór funkcji
. Wzór funkcji 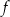 ma postać
ma postać
A) 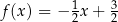 B)
B) 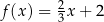
C) 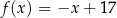 D)
D)