/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 20 kwietnia 2013 Czas pracy: 180 minut
Proste 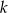 i
i 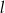 są równoległe do osi
są równoległe do osi 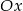 i przecinają wykres funkcji
i przecinają wykres funkcji 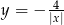 odpowiednio w punktach
odpowiednio w punktach 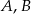 i
i 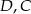 w ten sposób, że czworokąt
w ten sposób, że czworokąt 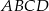 jest trapezem o polu 6 i wysokości 2. Oblicz obwód trapezu
jest trapezem o polu 6 i wysokości 2. Oblicz obwód trapezu 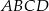 .
.
W skończonym ciągu geometrycznym 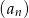 wyraz pierwszy jest równy 2, a wyraz ostatni 39 366. Wiedząc, że suma wszystkich wyrazów wynosi 59 048, oblicz iloraz tego ciągu.
wyraz pierwszy jest równy 2, a wyraz ostatni 39 366. Wiedząc, że suma wszystkich wyrazów wynosi 59 048, oblicz iloraz tego ciągu.
Rozwiąż układ równań 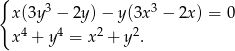
Na bokach 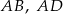 i
i 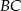 rombu
rombu 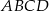 wybrano odpowiednio punkty
wybrano odpowiednio punkty 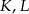 i
i 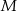 w ten sposób, że odcinki
w ten sposób, że odcinki 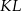 i
i 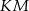 są równoległe do przekątnych rombu. Wykaż, że odcinek
są równoległe do przekątnych rombu. Wykaż, że odcinek 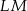 przechodzi przez punkt przecięcia przekątnych rombu.
przechodzi przez punkt przecięcia przekątnych rombu.
Rozwiąż równanie 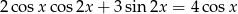 .
.
Dane są liczby wymierne 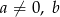 i
i 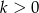 takie, że liczby
takie, że liczby 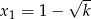 i
i 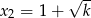 są pierwiastkami równania
są pierwiastkami równania 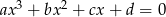 . Wykaż, że
. Wykaż, że  i
i 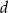 są liczbami wymiernymi.
są liczbami wymiernymi.
W trójkącie 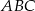 środkowa
środkowa 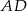 jest prostopadła do boku
jest prostopadła do boku 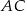 oraz
oraz 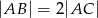 . Oblicz miarę kąta
. Oblicz miarę kąta 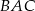 .
.
W układzie współrzędnych dany jest punkt 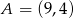 . Na okręgu o równaniu
. Na okręgu o równaniu 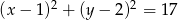 wyznacz współrzędne punktu
wyznacz współrzędne punktu 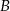 , dla którego odległość
, dla którego odległość 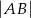 jest największa.
jest największa.
Wykaż, że jeżeli 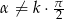 , gdzie
, gdzie 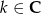 , to
, to
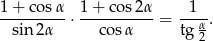
Ile jest liczb pięciocyfrowych, które mają trzy cyfry parzyste i dwie nieparzyste?
Podstawą ostrosłupa jest trójkąt równoboczny o boku długości 4, krawędzie boczne mają długości 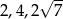 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.

