/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 13 kwietnia 2019 Czas pracy: 170 minut
Zadania zamknięte
Różnica 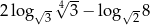 jest równa
jest równa
A) 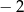 B)
B) 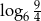 C)
C) 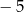 D) 7
D) 7
Liczba 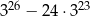 jest równa
jest równa
A) 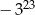 B)
B) 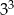 C)
C) 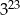 D)
D) 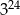
Jacek kupił 8 bułek po 0,65 zł za sztukę oraz 1,5 kilograma ogórków po 4,40 zł za kilogram. Oszacował, że za zakupy zapłacił w przybliżeniu 12 zł. Błąd względny tego przybliżenia wynosi:
A) 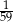 B) 0,2 C)
B) 0,2 C) 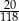 D) 11,8
D) 11,8
Narty po serii obniżek ceny o 5% kosztują 2606,42 zł. Oblicz ile razy obniżono cenę nart o 5% jeżeli ich cena po drugiej obniżce wynosiła 2888 zł.
A) 3 B) 4 C) 5 D) 6
Zbiorem wszystkich rozwiązań nierówności 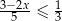 jest przedział
jest przedział
A) 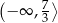 B)
B) 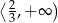 C)
C) 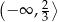 D)
D) 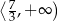
Równość 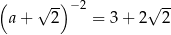 jest prawdziwa dla
jest prawdziwa dla
A) 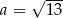 B)
B) 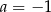 C)
C) 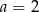 D)
D) 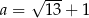
Liczbę 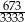 można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Trzydziestą cyfrą po przecinku jego rozwinięcia jest
można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Trzydziestą cyfrą po przecinku jego rozwinięcia jest
A) 2 B) 0 C) 1 D) 9
Rozwiązaniem równania 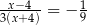 jest liczba
jest liczba
A) 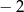 B) 2 C) 4 D)
B) 2 C) 4 D) 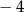
Wykresem funkcji kwadratowej 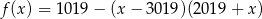 jest parabola, której wierzchołek leży na prostej
jest parabola, której wierzchołek leży na prostej
A) 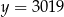 B)
B) 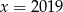 C)
C) 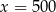 D)
D) 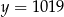
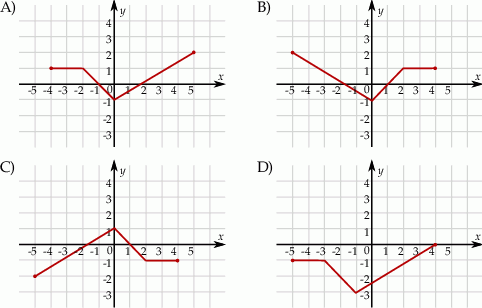
Rysunek przedstawia wykres funkcji 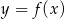 .
.
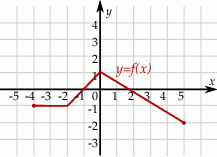
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 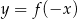 .
.
Wykres funkcji liniowej 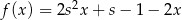 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 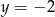 . Zatem
. Zatem
A) 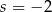 B)
B) 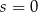 C)
C) 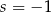 D)
D) 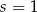
Największą wartością funkcji 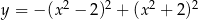 w przedziale
w przedziale 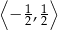 jest
jest
A) 0 B) 8 C) 4 D) 2
Dany jest ciąg geometryczny 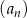 , określony dla
, określony dla 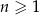 , w którym
, w którym 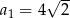 ,
, 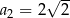 ,
, 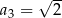 . Wzór na
. Wzór na  -ty wyraz tego ciągu ma postać
-ty wyraz tego ciągu ma postać
A) 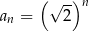 B)
B) 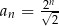 C)
C) 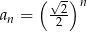 D)
D) 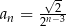
Układ równań 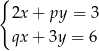 z niewiadomymi
z niewiadomymi  i
i 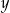 ma nieskończenie wiele rozwiązań. Zatem liczba
ma nieskończenie wiele rozwiązań. Zatem liczba 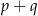 jest równa
jest równa
A) 6 B) 1 C) 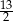 D)
D) 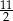
Odcinek 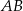 jest średnicą okręgu o środku
jest średnicą okręgu o środku 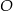 i promieniu
i promieniu  . Na tym okręgu wybrano punkt
. Na tym okręgu wybrano punkt 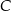 , taki, że
, taki, że 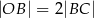 (zobacz rysunek).
(zobacz rysunek).
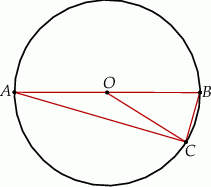
Pole trójkąta 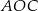 jest równe
jest równe
A) 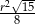 B)
B) 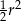 C)
C) 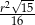 D)
D) 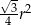
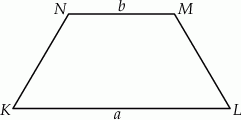
Dany jest trapez równoramienny 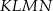 , którego podstawy mają długości
, którego podstawy mają długości 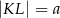 ,
, 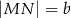 ,
, 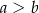 . Kąt
. Kąt 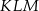 ma miarę
ma miarę 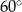 . Długość ramienia
. Długość ramienia 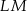 tego trapezu jest równa
tego trapezu jest równa
A) 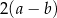 B)
B) 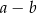 C)
C) 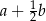 D)
D) 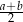
Ciąg arytmetyczny 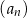 , określony dla
, określony dla 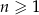 , spełnia warunek
, spełnia warunek 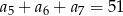 . Wtedy
. Wtedy
A) 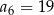 B)
B) 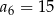 C)
C) 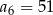 D)
D) 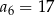
Wartość wyrażenia 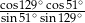 wynosi
wynosi
A) 1 B) 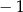 C)
C) 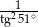 D)
D) 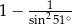
Miary dwóch kątów trapezu równoramiennego pozostają w stosunku 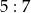 . Wynika stąd, że największy kąt tego trapezu ma miarę
. Wynika stąd, że największy kąt tego trapezu ma miarę
A) 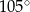 B)
B) 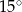 C)
C) 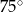 D)
D) 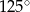
Boki równoległoboku 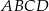 zwierają się w prostych o równaniach:
zwierają się w prostych o równaniach:
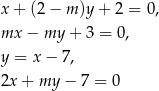
Zatem
A) 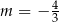 B)
B) 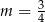 C)
C) 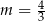 D)
D) 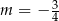
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt  , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy 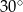 (zobacz rysunek).
(zobacz rysunek).
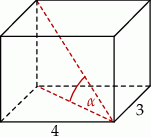
Wysokość graniastosłupa jest równa
A) 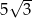 B)
B) 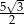 C)
C) 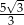 D)
D) 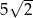
Wśród 200 osób przeprowadzono ankietę, w której zadano pytanie o liczbę filmów kinowych obejrzanych w ostatnim roku. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba filmów | 0 | 1 | 2 | 3 | 4 | 5 |
| Liczba osób | 57 | 79 | 38 | 17 | 7 | 2 |
Średnia liczba obejrzanych filmów przez jedną ankietowaną osobę jest równa
A) 2,44 B) 1,22 C) 1,88 D) 2,5
Przekrój osiowy walca jest prostokątem o przekątnej 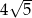 i polu 20. Pole powierzchni bocznej tego walca jest równe
i polu 20. Pole powierzchni bocznej tego walca jest równe
A) 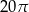 B)
B) 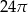 C)
C) 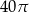 D)
D) 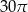
Punkty 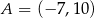 i
i 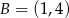 są końcami średnicy
są końcami średnicy 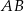 okręgu
okręgu  . Długość okręgu
. Długość okręgu  jest równa
jest równa
A) 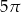 B)
B) 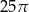 C)
C) 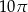 D)
D) 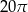
W pewnej loterii fantowej przygotowano dwie urny z losami, przy czym w drugiej urnie było trzy razy więcej losów niż w pierwszej urnie. Prawdopodobieństwo wybrania losu wygrywającego z pierwszej urny jest równe  , a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe
, a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe 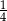 . Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
. Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
A)  B)
B) 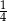 C)
C) 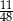 D)
D) 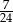
Zadania otwarte
Jeżeli do licznika i do mianownika dodatniego ułamka dodamy jego licznik, to otrzymamy  , a jeżeli do licznika i do mianownika dodamy 6, to otrzymamy
, a jeżeli do licznika i do mianownika dodamy 6, to otrzymamy 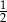 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Wykaż, że dla dowolnych liczb rzeczywistych 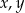 prawdziwa jest nierówność
prawdziwa jest nierówność
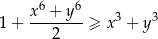
Wykresem funkcji kwadratowej 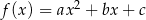 jest parabola styczna do prostej
jest parabola styczna do prostej 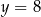 w punkcie
w punkcie 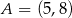 oraz przechodząca przez punkt
oraz przechodząca przez punkt 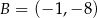 . Wyznacz wartości współczynników
. Wyznacz wartości współczynników 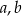 i
i  .
.
Okręgi o środkach odpowiednio 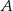 i
i 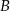 są styczne zewnętrznie i każdy z nich jest styczny do obu ramion danego kąta prostego (zobacz rysunek). Promień okręgu o środku
są styczne zewnętrznie i każdy z nich jest styczny do obu ramion danego kąta prostego (zobacz rysunek). Promień okręgu o środku 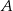 jest równy 1.
jest równy 1.
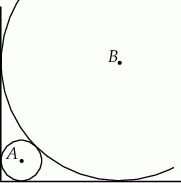
Uzasadnij, że promień okręgu o środku 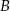 jest większy niż
jest większy niż 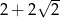 .
.
Kąt  jest ostry i
jest ostry i 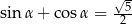 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 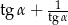 .
.
Punkty 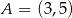 ,
, 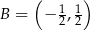 ,
, 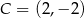 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 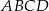 . Wyznacz równanie przekątnej
. Wyznacz równanie przekątnej 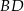 tego równoległoboku.
tego równoległoboku.
Ze zbioru 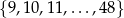 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3.
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3.
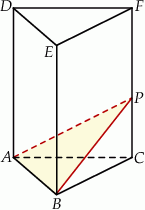
Krawędź podstawy graniastosłupa prawidłowego trójkątnego 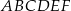 jest równa 6 (zobacz rysunek). Punkt
jest równa 6 (zobacz rysunek). Punkt 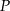 dzieli krawędź boczną
dzieli krawędź boczną 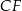 w stosunku
w stosunku 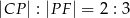 . Pole trójkąta
. Pole trójkąta 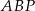 jest równe
jest równe 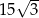 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Pole prostokąta 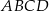 jest równe 60, a promień okręgu wpisanego w trójkąt
jest równe 60, a promień okręgu wpisanego w trójkąt 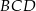 jest równy 2. Oblicz obwód tego prostokąta.
jest równy 2. Oblicz obwód tego prostokąta.

