/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 7 marca 2020 Czas pracy: 180 minut
Zadania zamknięte
Jeżeli 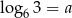 , to
, to 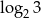 równa się
równa się
A) 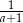 B)
B) 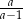 C)
C) 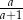 D)
D) 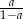
Dane są trzy niewspółliniowe punkty: 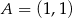 ,
, 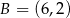 ,
, 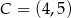 . Ile jest wszystkich punktów
. Ile jest wszystkich punktów 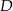 takich, że czworokąt o wierzchołkach w punktach
takich, że czworokąt o wierzchołkach w punktach 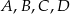 jest trapezem prostokątnym?
jest trapezem prostokątnym?
A) 1 B) 3 C) 6 D) 4
Funkcja homograficzna 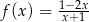 , gdzie
, gdzie 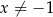 ,
,
A) jest rosnąca w zbiorze 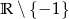 B) jest malejąca w zbiorze
B) jest malejąca w zbiorze 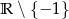
C) nie przyjmuje wartości 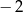 D) nie przyjmuje wartości 2
D) nie przyjmuje wartości 2
Niepuste zdarzenia losowe 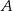 i
i 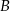 zawarte w
zawarte w 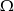 są takie, że
są takie, że 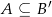 , gdzie
, gdzie 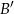 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 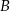 . Wynika stąd, że
. Wynika stąd, że
A) 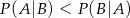 B)
B) 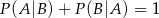
C) 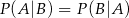 D)
D) 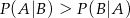
Suma szeregu geometrycznego: 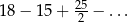 jest równa
jest równa
A) 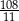 B) 33 C)
B) 33 C) 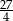 D) 108
D) 108
Zadania otwarte
Funkcja 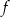 jest określona wzorem
jest określona wzorem 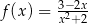 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie o odciętej
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie o odciętej 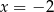 .
.
Udowodnij, że dla dowolnych dodatnich liczb rzeczywistych  i
i 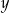 , takich że
, takich że 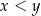 , i dowolnej dodatniej liczby rzeczywistej
, i dowolnej dodatniej liczby rzeczywistej 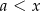 , prawdziwa jest nierówność
, prawdziwa jest nierówność 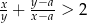 .
.
W pojemniku ze słodyczami znajduje się 48 cukierków i 32 lizaki. Osiem lizaków i piętnaście cukierków ma smak jabłkowy, a pozostałe słodycze mają smak pomarańczowy. Z pojemnika wybrano losowo jeden słodycz (cukierek lub lizak) i okazało się, że ma smak pomarańczowy. Oblicz prawdopodobieństwo zdarzenia, że wybrany słodycz jest lizakiem.
Oblicz granicę 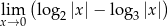 .
.
Ciągi 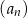 i
i 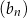 , gdzie
, gdzie 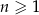 , są ciągami arytmetycznymi. Ciąg
, są ciągami arytmetycznymi. Ciąg 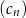 jest określony wzorem
jest określony wzorem 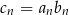 , dla
, dla 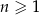 , a ciąg
, a ciąg 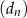 ciągiem różnic dwóch kolejnych wyrazów ciągu
ciągiem różnic dwóch kolejnych wyrazów ciągu 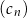 :
: 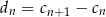 , dla
, dla 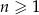 . Wykaż, że ciąg
. Wykaż, że ciąg 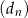 jest ciągiem arytmetycznym, którego różnica jest równa podwojonemu iloczynowi różnic ciągów
jest ciągiem arytmetycznym, którego różnica jest równa podwojonemu iloczynowi różnic ciągów 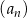 i
i 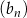 .
.
Ile jest liczb naturalnych siedmiocyfrowych, w których każde trzy cyfry stojące obok siebie są parami różne.
Rozwiąż równanie 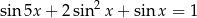 w przedziale
w przedziale 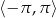 .
.
Wykaż, że jeżeli długości 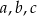 boków trójkąta spełniają równość
boków trójkąta spełniają równość
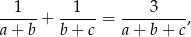
to promień okręgu opisanego na tym trójkącie jest równy 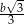 .
.
Tworząca stożka jest nachylona do podstawy pod kątem  . Kula opisana na tym stożku ma promień
. Kula opisana na tym stożku ma promień 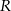 . Oblicz objętość tego stożka.
. Oblicz objętość tego stożka.
Ciąg 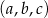 jest geometryczny, a ciągi
jest geometryczny, a ciągi 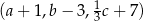 i
i 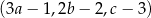 są arytmetyczne. Oblicz
są arytmetyczne. Oblicz 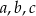 .
.
Punkt 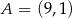 jest wierzchołkiem rombu
jest wierzchołkiem rombu 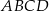 o polu 60. Przekątna
o polu 60. Przekątna 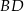 zawiera się w prostej
zawiera się w prostej 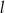 o równaniu
o równaniu 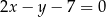 . Wyznacz równanie okręgu wpisanego w ten romb.
. Wyznacz równanie okręgu wpisanego w ten romb.
Koszt godziny pływania pewnego rodzaju łodzi jest sumą kosztu stałego i kosztu zmiennego zależnego od prędkości łodzi. Wiadomo, że koszt stały jest równy 2880 zł/h, a koszt zmienny 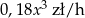 , gdzie
, gdzie 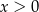 oznacza prędkość łodzi (w km/h).
oznacza prędkość łodzi (w km/h).
- Przy jakich prędkościach łodzi koszt przepłynięcia 1 km będzie mniejszy niż 306 zł?
- Przy jakiej prędkości łodzi koszt przepłynięcia 1 km będzie najmniejszy? Oblicz ten koszt.

