/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom podstawowy grupa II 29 maja 2013 Czas pracy: 170 minut
Zadania zamknięte
Liczba 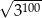 jest równa
jest równa
A) 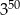 B) 320 C)
B) 320 C) 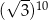 D)
D) 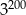
Wartość wyrażenia 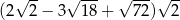 jest równa:
jest równa:
A) 2 B) 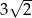 C)
C) 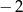 D) 1
D) 1
Liczba 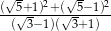 jest równa:
jest równa:
A) 4 B) 3 C) 8 D) 6
Wartość wyrażenia 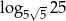 wynosi:
wynosi:
A)  B)
B) 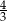 C)
C)  D)
D) 
Rozwinięcie dziesiętne skończone ma liczba:
A) 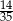 B)
B) 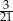 C)
C) 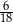 D)
D) 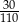
Cenę pewnego towaru obniżono o 25%. O ile procent należy podnieść obecną cenę tego towaru, aby otrzymać cenę początkową?
A) o 33,(3)% B) o 20% C) o 15,(2)% D) o 22%
Ile procent doby stanowi 15 minut?
A) 4% B) około 2% C) 12,5% D) około 1%
Jeżeli 35% pewnej liczby  jest równe 140 to
jest równe 140 to
A) 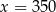 B)
B) 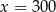 C)
C) 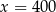 D)
D) 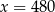
Rozwiązaniem nierówności 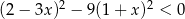 jest zbiór
jest zbiór
A) 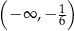 B)
B) 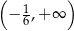 C)
C) 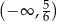 D)
D) 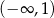
Wszystkie liczby spełniające warunek 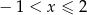 można zapisać za pomocą przedziału:
można zapisać za pomocą przedziału:
A) 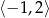 B)
B) 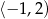 C)
C) 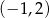 D)
D) 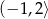
Rozwiązaniem równania 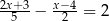 jest liczba:
jest liczba:
A) 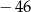 B) 32 C) 4 D) 6
B) 32 C) 4 D) 6
Dziedziną funkcji 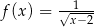 jest
jest
A) 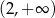 B)
B) 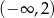 C)
C) 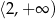 D)
D) 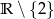
Ile miejsc zerowych ma funkcja
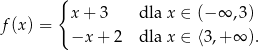
A) 0 B) 2 C) 1 D) 3
Funkcja 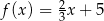 przyjmuje wartości dodatnie w przedziale:
przyjmuje wartości dodatnie w przedziale:
A) 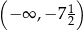 B)
B) 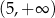 C)
C) 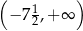 D)
D) 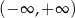
Prosta o równaniu 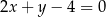 jest równoległa do prostej:
jest równoległa do prostej:
A) 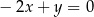 B)
B) 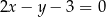 C)
C) 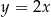 D)
D) 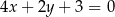
Miara kąta wpisanego opartego na  okręgu wynosi:
okręgu wynosi:
A) 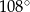 B)
B) 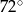 C)
C) 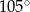 D)
D) 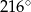
Większa część odcinka podzielonego na dwie części w stosunku 3:5 wynosi 20 cm. Długość tego odcinka wynosi:
A) 33 cm B) 27 cm C) 30 cm D) 32 cm
Wysokość rombu jest dwa razy krótsza od jego boku. Kąt rozwarty rombu ma miarę:
A) 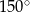 B)
B) 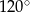 C)
C) 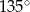 D)
D) 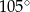
Z odcinków 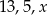 budujemy trójkąt. Będzie on prostokątny, gdy:
budujemy trójkąt. Będzie on prostokątny, gdy:
A) 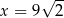 B)
B) 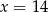 C)
C) 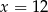 D)
D) 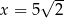
Trójkąty 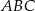 i
i 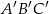 są podobne
są podobne 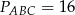 ,
, 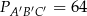 , wysokość
, wysokość 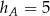 . Odpowiadająca jej wysokość w drugim trójkącie jest równa:
. Odpowiadająca jej wysokość w drugim trójkącie jest równa:
A) 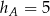 B)
B) 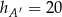 C)
C) 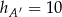 D) nie można określić
D) nie można określić
W trójkącie prostokątnym kąty ostre oznaczono  i
i 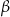 ,
, 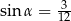 . Jaką miarę ma
. Jaką miarę ma 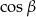 ?
?
A) 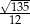 B)
B) 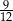 C)
C) 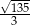 D)
D) 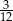
Korzystając ze wzorów redukcyjnych dowolnego kąta, oblicz 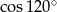
A) 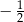 B)
B) 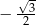 C)
C) 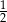 D)
D) 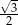
Miara kąta wewnętrznego ośmiokąta foremnego jest równa:
A) 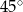 B)
B) 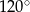 C)
C) 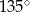 D)
D) 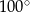
Zadania otwarte
Wykaż, że liczba 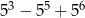 jest podzielna przez 101.
jest podzielna przez 101.
Wykaż, że 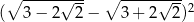 jest liczbą naturalną.
jest liczbą naturalną.
Trójkąt prostokątny ma przyprostokątne długości 6 i 8. Wyznacz długość najkrótszej wysokości tego trójkąta.
Roczne oprocentowanie lokaty, które wynosiło 8%, zmniejszono o 37,5%. Oblicz, o ile punktów procentowych zmniejszono to oprocentowanie.
Rozwiąż równanie 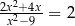 .
.
Trójkąt o bokach 12, 9 i 15 jest podobny do trójkąta o obwodzie 108. Oblicz długości boków drugiego trójkąta.
Zmieszano 2 kg solanki o zawartości 12% soli i 1 kg solanki o zawartości 18% soli. Ile procent soli zawiera ta mieszanina?
Na przedstawienie sprzedano 300 biletów po 15 zł i 20 zł. Po potrąceniu 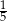 kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4176 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4176 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
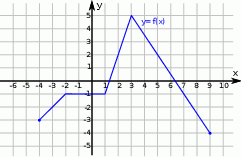
Na rysunku jest przedstawiony wykres funkcji 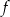 .
.
- Naszkicuj wykres funkcji
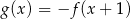 .
. - Określ dziedzinę
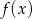 i
i 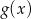 .
. - Podaj maksymalne przedziały, w których funkcja
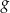 jest malejąca.
jest malejąca. - Podaj wartość funkcji
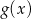 dla argumentu równego 2.
dla argumentu równego 2.