/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 11 marca 2023 Czas pracy: 180 minut
Klient wpłacił do banku 40 000 zł na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości 2% od kwoty bieżącego kapitału znajdującego się na lokacie. Po 3 latach oszczędzania w tym banku kwota na lokacie (bez uwzględniania podatków) jest równa
A) 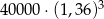 B)
B) 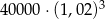 C)
C) 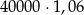 D)
D) 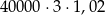
Wartość wyrażenia 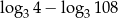 jest równa
jest równa
A) 2 B) 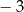 C) 3 D)
C) 3 D) 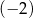
Informacja do zadań 3.1 i 3.2
Funkcja kwadratowa 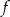 jest określona wzorem
jest określona wzorem 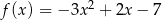 .
.
Wykresem funkcji 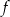 jest parabola, której wierzchołek leży na prostej o równaniu
jest parabola, której wierzchołek leży na prostej o równaniu
A) 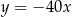 B)
B) 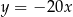 C)
C) 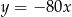 D)
D) 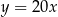
Jeżeli przesuniemy wykres funkcji 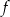 o dwie jednostki 2 lewo, to otrzymamy wykres funkcji
o dwie jednostki 2 lewo, to otrzymamy wykres funkcji
A) 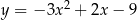 B)
B) 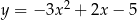
C) 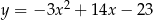 D)
D) 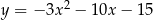
Wskaż nierówność, której zbiór wszystkich rozwiązań zaznaczono na osi liczbowej.
![]()
A) 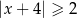 B)
B) 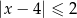 C)
C) 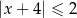 D)
D) 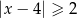
Wyznacz największą liczbę rzeczywistą spełniającą równanie
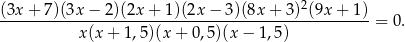
Na rysunku jest przedstawiony fragment wykresu funkcji 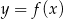 .
.
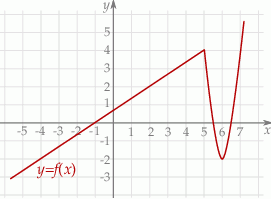
W przedziale 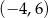 równanie
równanie 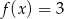
A) nie ma rozwiązań.
B) ma dokładnie dwa rozwiązania.
C) ma dokładnie trzy rozwiązania.
D) ma nieskończenie wiele rozwiązań.
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 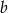 prawdziwa jest nierówność
prawdziwa jest nierówność
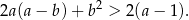
W ciągu trzech godzin dwie jednakowe maszyny produkują razem 1200 guzików. Ile guzików wyprodukuje pięć takich maszyn w ciągu dwóch godzin? Przyjmij, że maszyny pracują z taką samą, stałą wydajnością.
A) 2000 B) 900 C) 1000 D) 1500
Dana jest nierówność kwadratowa
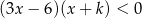
z niewiadomą  i parametrem
i parametrem 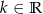 . Rozwiązaniem tej nierówności jest przedział
. Rozwiązaniem tej nierówności jest przedział 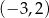 . Liczba
. Liczba 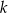 jest równa
jest równa
A) 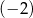 B) 2 C)
B) 2 C) 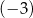 D) 3
D) 3
Objętość sześcianu 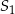 jest równa
jest równa 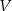 , a objętość sześcianu
, a objętość sześcianu 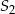 jest równa
jest równa 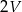 . Pole powierzchni całkowitej sześcianu
. Pole powierzchni całkowitej sześcianu 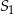 jest równe
jest równe 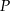 .
.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1, 2 albo 3.
Pole powierzchni całkowitej sześcianu 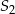 jest równe
jest równe
A) 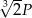 , , | B) 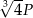 , , |
| ponieważ stosunek pól powierzchni brył podobnych jest równy | |
| 1) | sześcianowi skali podobieństwa. |
| 2) | skali podobieństwa. |
| 3) | kwadratowi skali podobieństwa. |
Dany jest wielomian 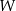 określony wzorem
określony wzorem 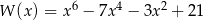 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wielomian
. Wielomian 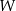 przy rozkładzie na czynniki ma postać
przy rozkładzie na czynniki ma postać
A) 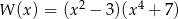 B)
B) 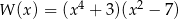
C) 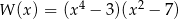 D)
D) 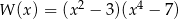
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 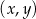 , dana jest prosta
, dana jest prosta 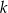 o równaniu
o równaniu 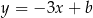 , przechodząca przez punkt
, przechodząca przez punkt 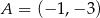 . Współczynnik
. Współczynnik 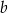 w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 0 B) 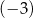 C)
C) 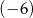 D)
D) 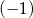
Liczba 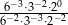 jest równa
jest równa
A) 6 B) 3 C) 24 D) 2
Na wykresie funkcji 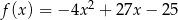 wyznacz taki punkt
wyznacz taki punkt 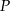 , którego druga współrzędna jest 7 razy większa od pierwszej współrzędnej.
, którego druga współrzędna jest 7 razy większa od pierwszej współrzędnej.
Kąt  jest rozwarty oraz
jest rozwarty oraz 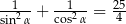 . Wartość wyrażenia
. Wartość wyrażenia 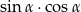 jest równa
jest równa
A) 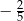 B)
B)  C)
C) 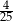 D)
D) 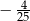
Ciąg 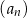 jest określony wzorem
jest określony wzorem 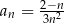 dla każdej liczby naturalnej
dla każdej liczby naturalnej 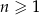 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 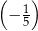 B)
B) 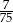 C)
C) 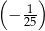 D)
D) 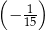
Informacja do zadań 17.1 i 17.2
Na boku 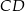 prostokąta
prostokąta 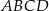 wybrano punkt
wybrano punkt 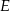 taki, że
taki, że 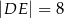 . Przekątna
. Przekątna 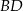 i odcinek
i odcinek 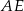 przecinają się w punkcie
przecinają się w punkcie 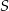 oraz
oraz 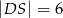 . Bok
. Bok 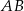 prostokąta
prostokąta 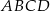 ma długość 12 (zobacz rysunek).
ma długość 12 (zobacz rysunek).
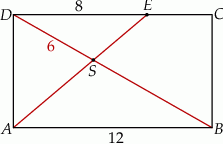
Oblicz długość odcinka 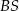 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 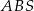 jest 5 razy mniejsze od pola prostokąta jest 5 razy mniejsze od pola prostokąta 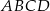 . . | P | F |
Obwód trójkąta 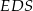 stanowi stanowi  obwodu trójkąta obwodu trójkąta 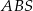 . . | P | F |
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 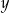 wyrażenie
wyrażenie
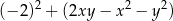
jest równe
A) ![[2− (x− y)]2](https://img.zadania.info/zes/0070258/HzesT101x.gif) B)
B) ![− [(x − y) − 2]⋅ [(x − y )+ 2]](https://img.zadania.info/zes/0070258/HzesT102x.gif)
C) ![[2− (x− y)]⋅[2 + (x − y)]](https://img.zadania.info/zes/0070258/HzesT103x.gif) D)
D) ![[2 − (x + y)]2](https://img.zadania.info/zes/0070258/HzesT104x.gif)
E) ![[2− (x+ y)]⋅[2+ (x+ y)]](https://img.zadania.info/zes/0070258/HzesT105x.gif) F)
F) ![[2 + (x − y)]2](https://img.zadania.info/zes/0070258/HzesT106x.gif)
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 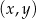 , dane są:
, dane są:
– prosta 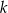 o równaniu
o równaniu 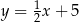
– prosta 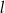 o równaniu
o równaniu 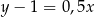 .
.
Proste 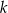 i
i 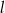
A) pokrywają się. B) nie mają punktów wspólnych.
C) są prostopadłe. D) przecinają się pod kątem 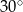 .
.
Punkty 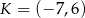 i
i 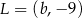 są końcami odcinka
są końcami odcinka 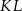 . Pierwsza współrzędna środka odcinka
. Pierwsza współrzędna środka odcinka 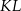 jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że
jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że
A) 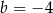 B)
B) 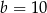 C)
C) 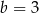 D)
D) 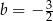
Dany jest rosnący ciąg 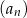 określony dla
określony dla 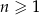 , którego wyrazami są wszystkie liczby trzycyfrowe podzielne przez 17. Dziewiętnasty wyraz tego ciągu jest równy
, którego wyrazami są wszystkie liczby trzycyfrowe podzielne przez 17. Dziewiętnasty wyraz tego ciągu jest równy
A) 425 B) 323 C) 408 D) 493
Trawnik ma kształt trójkąta równoramiennego o podstawie 80 m i ramionach długości 50 m. Z powierzchni trawnika postanowiono wydzielić prostokątny plac zabaw w ten sposób, że dwa z wierzchołków tego prostokąta leżą na podstawie, a pozostałe dwa na ramionach trójkąta ograniczającego trawnik (zobacz rysunek).
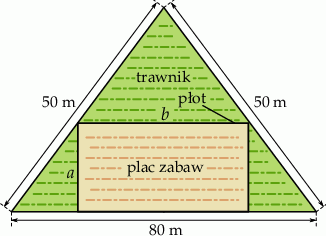
Oblicz wymiary  i
i 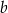 placu zabaw, tak, aby jego pole było największe możliwe.
placu zabaw, tak, aby jego pole było największe możliwe.
Punkty 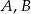 oraz
oraz 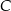 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 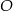 . Kąt
. Kąt 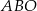 ma miarę
ma miarę 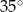 , a kąt
, a kąt 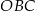 ma miarę
ma miarę 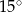 (zobacz rysunek).
(zobacz rysunek).
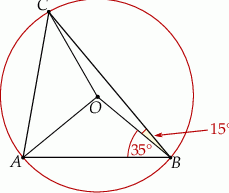
Miara kąta 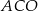 jest równa
jest równa
A) 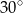 B)
B) 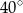 C)
C) 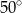 D)
D) 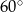
Ze zbioru liczb 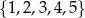 losujemy kolejno trzy razy po jednej liczbie ze zwracaniem tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie ze zwracaniem tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia 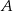 – otrzymana liczba jest cztery razy większa od kwadratu liczby naturalnej.
– otrzymana liczba jest cztery razy większa od kwadratu liczby naturalnej.
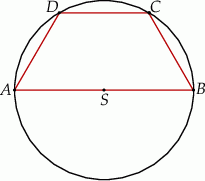
Informacja do zadań 25.1 i 25.2
W okręgu o promieniu 6 poprowadzono cięciwę 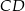 równoległą do średnicy
równoległą do średnicy 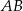 tego okręgu i taką, że
tego okręgu i taką, że 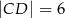 (zobacz rysunek).
(zobacz rysunek).
Odległość cięciwy 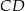 od średnicy
od średnicy 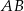 jest równa
jest równa
A) 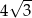 B)
B) 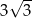 C)
C) 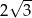 D) 4
D) 4
Obwód trapezu 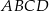 jest równy
jest równy
A) 30 B) 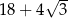 C)
C) 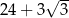 D) 32
D) 32
Liczba 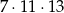 ma
ma
A) tylko pięć dzielników naturalnych B) tylko sześć dzielników naturalnych
C) tylko siedem dzielników naturalnych D) tylko osiem dzielników naturalnych
W układzie współrzędnych dany jest okrąg  o równaniu
o równaniu
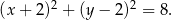
Okrąg  przecina prostą
przecina prostą 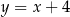 w punktach o współrzędnych
w punktach o współrzędnych
A) 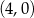 i
i 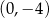 B)
B) 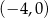 i
i 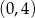
C) 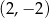 i
i 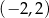 D)
D) 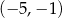 i
i 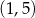
Wszystkie liczby trzycyfrowe uporządkowano malejąco. Mediana otrzymanego w ten sposób zestawu danych jest równa
A) 549,5 B) 550 C) 501 D) 599,5
Na loterii stosunek liczby losów wygrywających do liczby losów przegrywających jest równy 2 : 7. Zakupiono jeden los z tej loterii. Prawdopodobieństwo zdarzenia polegającego na tym, że zakupiony los jest przegrywający, jest równe
A)  B)
B)  C)
C) 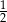 D)
D) 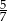
W graniastosłupie prawidłowym sześciokątnym 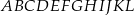 wierzchołki
wierzchołki 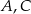 i
i 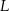 połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.
połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.
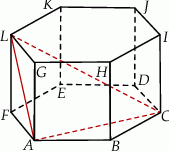
Cosinus największego kąta trójkąta 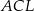 jest równy
jest równy
A)  B)
B) 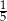 C) 0 D)
C) 0 D) 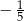
Przekątne trapezu 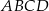 przecinają się w punkcie
przecinają się w punkcie 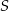 , jego podstawy mają długości
, jego podstawy mają długości 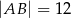 i
i 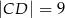 , a wysokość trapezu ma długość 8. Punkt
, a wysokość trapezu ma długość 8. Punkt 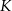 jest środkiem odcinka
jest środkiem odcinka 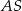 (zobacz rysunek).
(zobacz rysunek).
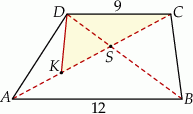
Oblicz pole trójkąta 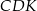 .
.
Informacja do zadań 32.1 i 32.2
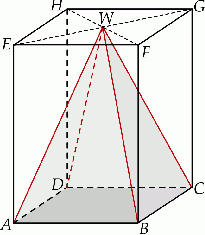
Dany jest graniastosłup prawidłowy czworokątny 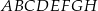 o krawędzi podstawy równej 9 i wysokości równej 12. Wierzchołki podstawy
o krawędzi podstawy równej 9 i wysokości równej 12. Wierzchołki podstawy 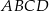 graniastosłupa połączono odcinkami z punktem
graniastosłupa połączono odcinkami z punktem 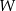 , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy 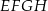 . Otrzymano w ten sposób ostrosłup prawidłowy czworokątny
. Otrzymano w ten sposób ostrosłup prawidłowy czworokątny  .
.
Objętość 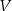 ostrosłupa
ostrosłupa 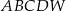 jest równa
jest równa
A) 972 B) 162 C) 324 D) 243
Oblicz cosinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.

