/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 9 marca 2013 Czas pracy: 170 minut
Zadania zamknięte
Liczba 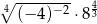 jest równa
jest równa
A) 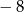 B) 8 C)
B) 8 C) 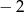 D) 4
D) 4
Wskaż liczbę, która spełnia równanie 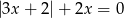 .
.
A) 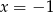 B)
B) 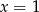 C)
C) 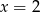 D)
D) 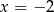
Liczba 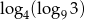 jest równa
jest równa
A) 1 B) 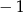 C)
C) 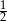 D)
D) 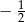
Liczba 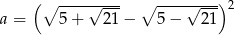 jest równa
jest równa
A) 4 B) 6 C) 10 D) 14
Wierzchołek paraboli będącej wykresem funkcji 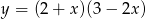 ma współrzędne
ma współrzędne
A) 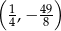 B)
B) 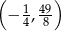 C)
C) 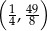 D)
D) 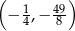
Liczby 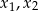 są różnymi rozwiązaniami równania
są różnymi rozwiązaniami równania 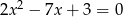 . Iloczyn
. Iloczyn 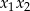 jest równy
jest równy
A) 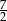 B)
B)  C)
C)  D)
D) 
Do 4 kg roztworu soli o stężeniu 10% dosypano pół kilograma soli. Stężenie procentowe nowego roztworu wynosi
A) 22,5% B) 40% C) 20% D) 36%
Zbiorem rozwiązań nierówności 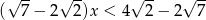 jest przedział
jest przedział
A) 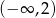 B)
B) 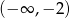 C)
C) 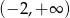 D)
D) 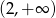
Cięciwa okręgu ma długość 24 cm i jest oddalona od jego środka o 5 cm. Promień tego okręgu ma długość
A) 13 cm B) 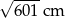 C) 5 cm D)
C) 5 cm D) 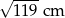
Liczba 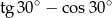 jest równa
jest równa
A) 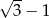 B)
B) 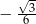 C)
C) 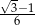 D)
D) 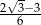
Do wykresu funkcji liniowej 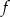 należą punkty
należą punkty 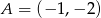 i
i 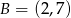 . Funkcja
. Funkcja 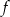 ma wzór
ma wzór
A) 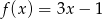 B)
B) 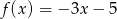 C)
C) 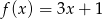 D)
D) 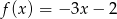
Liczba miejsc zerowych funkcji
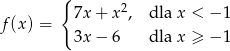
jest równa
A) 0 B) 1 C) 2 D) 3
Okrąg o równaniu 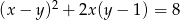 ma promień równy
ma promień równy
A) 9 B) 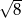 C) 3 D) 8
C) 3 D) 8
Odcinki 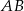 i
i 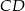 są równoległe i
są równoległe i 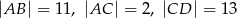 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 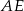 jest równa
jest równa
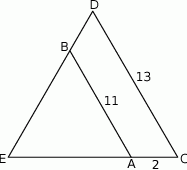
A) 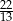 B)
B) 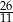 C) 11 D) 13
C) 11 D) 13
W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy
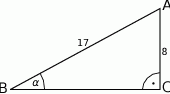
A) 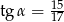 B)
B) 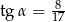 C)
C) 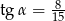 D)
D) 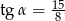
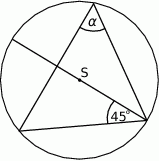
Punkt 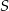 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
A) 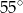 B)
B) 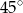 C)
C) 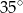 D)
D) 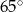
Wiadomo, że dziedziną funkcji 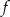 określonej wzorem
określonej wzorem 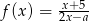 jest zbiór
jest zbiór 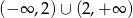 . Wówczas
. Wówczas
A) 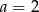 B)
B) 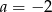 C)
C) 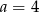 D)
D) 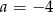
Dany jest ciąg 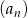 określony wzorem
określony wzorem 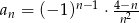 dla
dla 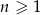 . Wówczas wyraz
. Wówczas wyraz 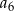 tego ciągu jest równy
tego ciągu jest równy
A) 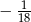 B)
B) 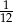 C)
C) 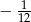 D)
D) 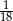
W ciągu geometrycznym 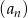 dane są:
dane są: 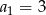 i
i 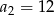 . Wtedy
. Wtedy
A) 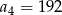 B)
B) 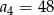 C)
C) 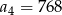 D)
D) 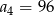
W kolejnych dziewięciu rzutach kostką otrzymano następujące wyniki: 3, 5, 1, 3, 4, 6, 5, 2, 5. Mediana tych wyników jest równa:
A) 5 B) 4 C) 3,5 D) 3
Punkt 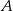 ma współrzędne
ma współrzędne 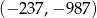 . Punkt
. Punkt 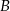 jest symetryczny do punktu
jest symetryczny do punktu 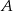 względem początku układu współrzędnych, a punkt
względem początku układu współrzędnych, a punkt 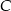 jest symetryczny do punktu
jest symetryczny do punktu 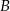 względem osi
względem osi 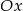 . Punkt
. Punkt 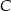 ma współrzędne
ma współrzędne
A) 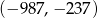 B)
B) 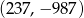 C)
C) 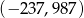 D)
D) 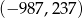
Przekrój osiowy walca jest kwadratem o boku  . Jeżeli
. Jeżeli 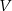 oznacza objętość walca,
oznacza objętość walca, 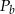 oznacza pole powierzchni bocznej walca, to
oznacza pole powierzchni bocznej walca, to
A) 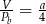 B)
B) 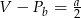 C)
C) 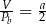 D)
D) 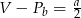
Ze zbioru liczb naturalnych zawartych w przedziale 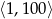 wybieramy losowo jedną. Niech
wybieramy losowo jedną. Niech 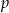 oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 6. Wówczas
oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 6. Wówczas
A) 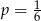 B)
B) 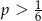 C)
C) 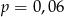 D)
D) 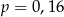
Zadania otwarte
Rozwiąż nierówność: 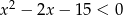 .
.
Rozwiąż równanie 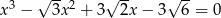 .
.
Udowodnij, że dowolne liczby rzeczywiste  i
i 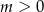 spełniają nierówność
spełniają nierówność
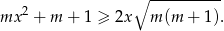
Czwarty wyraz ciągu arytmetycznego jest równy 8. Suma pięciu pierwszych wyrazów tego ciągu jest równa 15. Oblicz siódmy wyraz tego ciągu.
Punkt 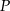 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 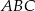 oraz
oraz 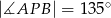 . Wykaż, że trójkąt
. Wykaż, że trójkąt  jest prostokątny.
jest prostokątny.
Spośród wierzchołków graniastosłupa sześciokątnego prostego losujemy jeden wierzchołek z dolnej podstawy i jeden wierzchołek z górnej podstawy. Oblicz prawdopodobieństwo tego, że wylosowane wierzchołki są końcami krawędzi bocznej graniastosłupa.
Punkty 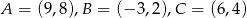 są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka 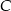 przecina prostą
przecina prostą 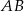 w punkcie
w punkcie 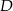 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 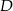 .
.
W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 6, a krawędź podstawy ma długość 3. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
Klasa IIIb liczy o jednego ucznia więcej niż klasa IIIa. Na koniec roku okazało się, że suma ocen z matematyki uzyskanych przez uczniów klasy IIIa jest równa 97,5 i jest jednocześnie równa sumie ocen z matematyki uzyskanych przez uczniów klasy IIIb. Gdy obliczono średnie z tych ocen w każdej z klas to okazało się, że średnia w klasie IIIa była wyższa o 0,15 niż średnia uzyskana w klasie IIIb. Oblicz ilu uczniów liczą obie klasy.

