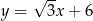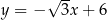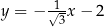/Szkoła średnia/Zadania maturalne
Poprawkowy Egzamin Maturalny
z Matematyki poziom podstawowy 22 sierpnia 2023 Czas pracy: 180 minut
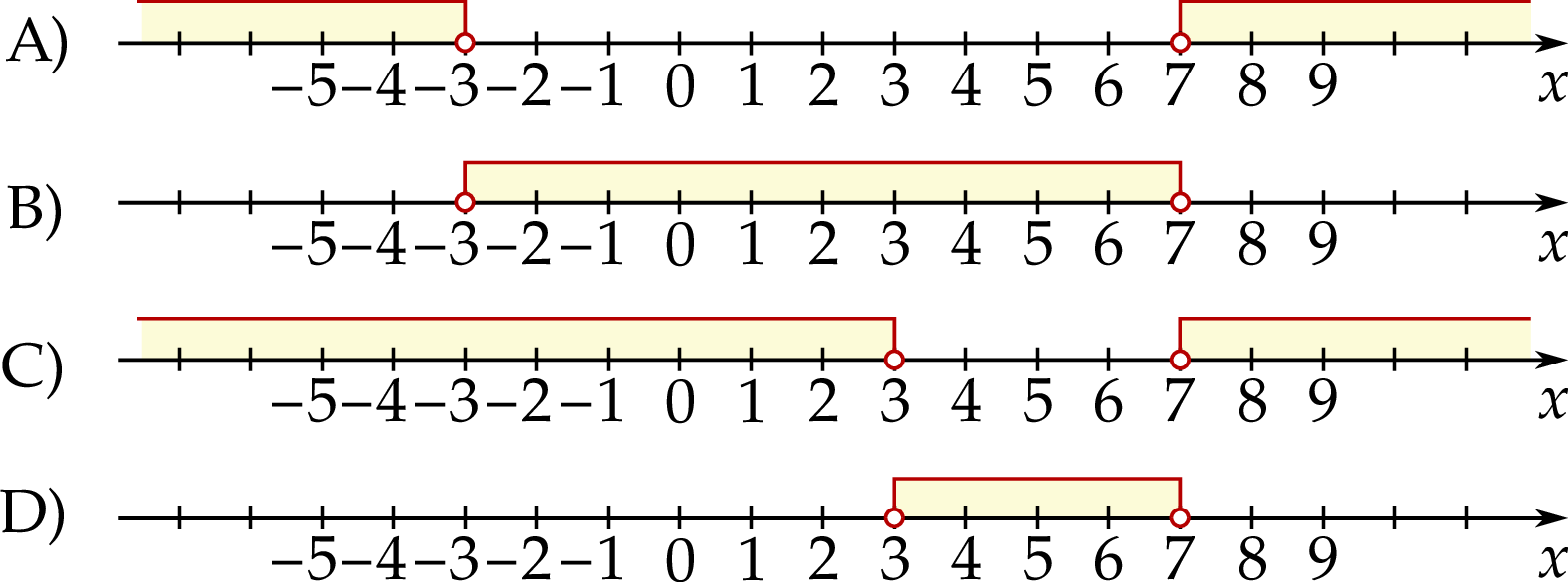
Dana jest nierówność
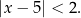
Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających powyższą nierówność?
Liczba 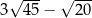 jest równa
jest równa
A) 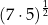 B)
B) 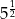 C) 7 D)
C) 7 D) 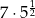
Liczba 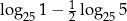 jest równa
jest równa
A) 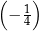 B)
B) 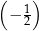 C)
C) 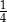 D)
D) 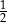
Wykaż, że dla każdej liczby naturalnej 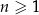 liczba
liczba 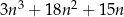 jest podzielna przez 6.
jest podzielna przez 6.
Wartość wyrażenia 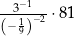 jest równa
jest równa
A) 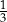 B)
B)  C) 3 D)
C) 3 D) 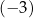
Wartość wyrażenia 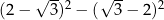 jest równa
jest równa
A) 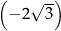 B) 0 C) 6 D)
B) 0 C) 6 D) 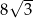
Dla każdej liczby rzeczywistej  różnej od 0 wartość wyrażenia
różnej od 0 wartość wyrażenia 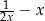 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A)  B)
B) 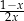 C)
C) 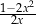 D)
D) 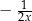
Równanie 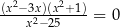 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie.
B) dwa rozwiązania.
C) trzy rozwiązania.
D) cztery rozwiązania.
Rozwiąż równanie 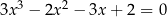 .
.
W kartezjańskim układzie współrzędnych 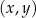 , punkt
, punkt 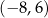 jest punktem przecięcia prostych o równaniach
jest punktem przecięcia prostych o równaniach
A) 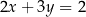 i
i 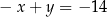 B)
B) 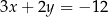 i
i 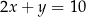
C) 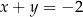 i
i 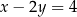 D)
D) 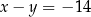 i
i 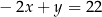
Miejscem zerowym funkcji liniowej 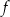 jest liczba 1. Wykres tej funkcji przechodzi przez punkt
jest liczba 1. Wykres tej funkcji przechodzi przez punkt 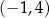 . Wzór funkcji
. Wzór funkcji 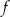 ma postać
ma postać
A) 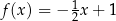 B)
B) 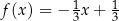
C) 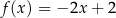 D)
D) 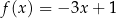
Funkcja 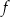 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  wzorem
wzorem 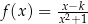 , gdzie
, gdzie 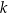 jest pewną liczbą rzeczywistą. Ta funkcja spełnia warunek
jest pewną liczbą rzeczywistą. Ta funkcja spełnia warunek 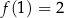 . Wartość współczynnika
. Wartość współczynnika 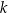 we wzorze tej funkcji jest równa
we wzorze tej funkcji jest równa
A) 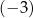 B) 3 C)
B) 3 C) 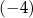 D) 4
D) 4
Funkcja kwadratowa 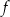 jest określona wzorem
jest określona wzorem 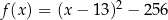 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 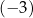 . Drugim miejscem zerowym funkcji
. Drugim miejscem zerowym funkcji 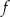 jest liczba
jest liczba
A) 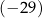 B)
B) 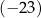 C) 23 D) 29
C) 23 D) 29
Informacja do zadań 14.1 – 14.3
W kartezjańskim układzie współrzędnych  narysowano wykres funkcji
narysowano wykres funkcji  (zobacz rysunek).
(zobacz rysunek).
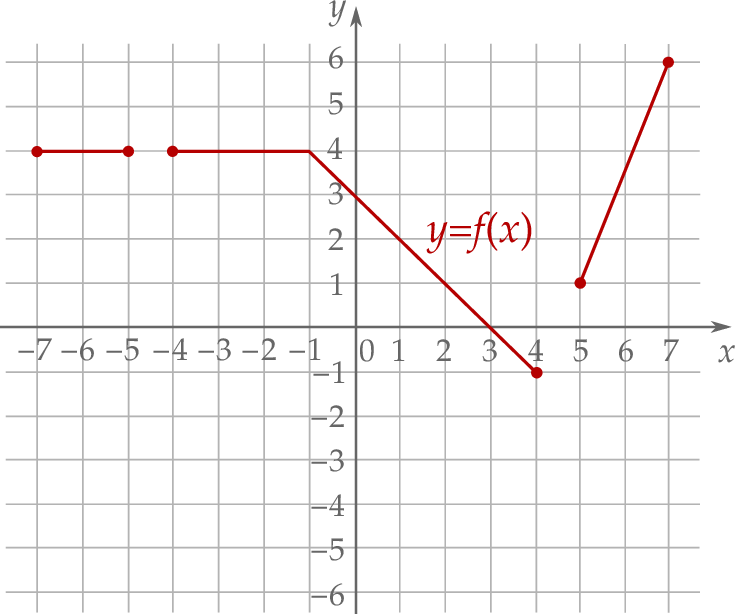
Funkcja 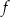 jest rosnąca w przedziale
jest rosnąca w przedziale
A) ![[− 5,4]](https://img.zadania.info/zes/0070541/HzesT63x.png) B)
B) ![[5 ,7]](https://img.zadania.info/zes/0070541/HzesT64x.png) C)
C) ![[1,5]](https://img.zadania.info/zes/0070541/HzesT65x.png) D)
D) ![[− 1,5]](https://img.zadania.info/zes/0070541/HzesT66x.png)
Wyznacz zbiór wszystkich argumentów, dla których funkcja 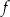 przyjmuje wartości większe od 1.
przyjmuje wartości większe od 1.
Funkcja 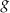 jest określona za pomocą funkcji
jest określona za pomocą funkcji 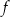 następująco:
następująco: 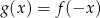 dla każdego
dla każdego ![x ∈ [− 7,− 5] ∪ [− 4,4 ]∪ [5 ,7]](https://img.zadania.info/zes/0070541/HzesT71x.png) . Na jednym z rysunków A–D przedstawiono, w kartezjańskim układzie współrzędnych
. Na jednym z rysunków A–D przedstawiono, w kartezjańskim układzie współrzędnych 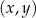 , wykres funkcji
, wykres funkcji 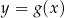 . Wykres funkcji
. Wykres funkcji 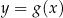 przedstawiono na rysunku
przedstawiono na rysunku
Funkcje  oraz
oraz  są określone dla każdej liczby rzeczywistej
są określone dla każdej liczby rzeczywistej  . Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Przedział ![(− ∞ ,2]](https://img.zadania.info/zes/0070541/HzesT79x.png) jest zbiorem wartości funkcji
jest zbiorem wartości funkcji
A) 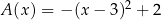 B)
B) 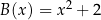 C)
C) 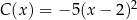
D) 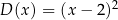 E)
E) 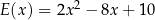 F)
F) 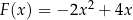
Ciąg 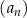 jest określony wzorem
jest określony wzorem 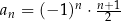 dla każdej liczby naturalnej
dla każdej liczby naturalnej 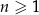 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) 2 B) 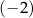 C) 3 D)
C) 3 D) 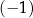
Dany jest ciąg geometryczny 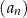 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 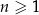 . Pierwszy wyraz tego ciągu jest równy 128, natomiast iloraz ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy 128, natomiast iloraz ciągu jest równy 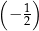 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wyraz 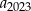 jest liczbą ujemną. jest liczbą ujemną. | P | F |
Różnica  jest równa 96. jest równa 96. | P | F |
Ciąg 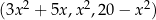 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz  .
.
Kąt  jest ostry i
jest ostry i 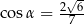 . Sinus kąta
. Sinus kąta  jest równy
jest równy
A) 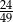 B)
B)  C)
C) 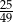 D)
D) 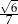
Trapez 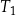 , o polu równym 52 i obwodzie 36, jest podobny do trapezu
, o polu równym 52 i obwodzie 36, jest podobny do trapezu 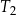 . Pole trapezu
. Pole trapezu 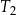 jest równe 13. Obwód trapezu
jest równe 13. Obwód trapezu 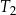 jest równy
jest równy
A) 18 B) 9 C) 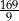 D)
D) 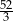
Koło ma promień równy 3. Obwód wycinka tego koła o kącie środkowym 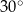 jest równy
jest równy
A) 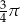 B)
B) 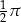 C)
C) 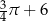 D)
D) 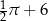
W okręgu 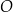 kąt środkowy
kąt środkowy 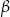 oraz kąt wpisany
oraz kąt wpisany  są oparte na tym samym łuku. Kąt
są oparte na tym samym łuku. Kąt 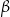 ma miarę o
ma miarę o 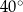 większą od kąta
większą od kąta  . Miara kąta
. Miara kąta 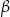 jest równa
jest równa
A) 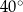 B)
B) 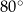 C)
C) 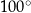 D)
D) 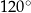
W trójkącie 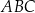 długość boku
długość boku 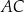 jest równa 3, a długość boku
jest równa 3, a długość boku 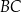 jest równa 4. Dwusieczna kąta
jest równa 4. Dwusieczna kąta 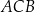 przecina bok
przecina bok 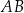 w punkcie
w punkcie 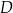 . Stosunek
. Stosunek 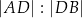 jest równy
jest równy
A) 4 : 3 B) 4 : 7 C) 3 : 4 D) 3 : 7
Dany jest trapez równoramienny 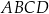 , w którym podstawa
, w którym podstawa 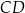 ma długość 6, ramię
ma długość 6, ramię 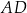 ma długość 4, a kąty
ma długość 4, a kąty 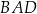 oraz
oraz 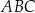 mają miarę
mają miarę 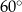 (zobacz rysunek).
(zobacz rysunek).
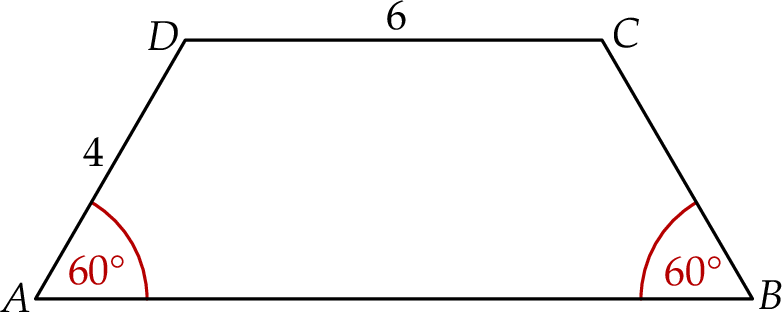
Oblicz pole tego trapezu.
W kartezjańskim układzie współrzędnych  dane są prosta
dane są prosta  o równaniu
o równaniu 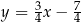 oraz punkt
oraz punkt 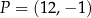 . Prosta przechodząca przez punkt
. Prosta przechodząca przez punkt 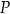 i równoległa do prostej
i równoległa do prostej 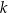 ma równanie
ma równanie
A) 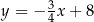 B)
B) 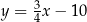 C)
C) 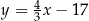 D)
D) 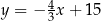
W kartezjańskim układzie współrzędnych 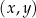 dany jest okrąg
dany jest okrąg 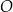 o środku
o środku 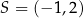 i promieniu 3. Okrąg
i promieniu 3. Okrąg 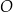 jest określony równaniem
jest określony równaniem
A) 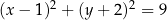 B)
B) 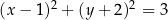
C) 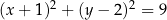 D)
D) 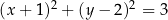
W kartezjańskim układzie współrzędnych 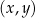 proste o równaniach:
proste o równaniach:
przecinają się w punktach, które są wierzchołkami trójkąta 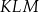 .
.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1, 2 albo 3.
Trójkąt 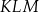 jest
jest
| A) równoramienny, | B) prostokątny, |
ponieważ
| 1) | oś 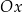 przechodzi przez jeden z wierzchołków tego trójkąta i środek jednego z boków tego trójkąta. przechodzi przez jeden z wierzchołków tego trójkąta i środek jednego z boków tego trójkąta. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | oś 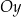 zawiera dwusieczną tego trójkąta. zawiera dwusieczną tego trójkąta. |
W kartezjańskim układzie współrzędnych 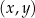 punkt
punkt 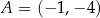 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 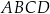 . Punkt
. Punkt 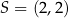 jest środkiem symetrii tego równoległoboku. Długość przekątnej
jest środkiem symetrii tego równoległoboku. Długość przekątnej 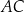 równoległoboku
równoległoboku 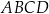 jest równa
jest równa
A) 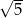 B)
B) 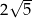 C)
C) 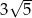 D)
D) 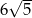
Informacja do zadań 29.1 i 29.2
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6.
Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 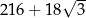 B)
B) 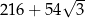 C)
C) 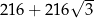 D)
D) 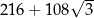
Oblicz cosinus kąta nachylenia dłuższej przekątnej tego graniastosłupa do płaszczyzny podstawy graniastosłupa.
Wszystkich różnych liczb naturalnych czterocyfrowych, w których zapisie dziesiętnym wszystkie cyfry są różne, jest
A) 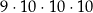 B)
B) 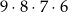 C)
C) 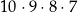 D)
D) 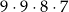
Ze zbioru pięciu liczb 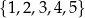 losujemy bez zwracania kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia
losujemy bez zwracania kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia 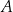 polegającego na tym, że obie wylosowane liczby są nieparzyste.
polegającego na tym, że obie wylosowane liczby są nieparzyste.
Na diagramie przedstawiono rozkład wynagrodzenia brutto wszystkich stu pracowników pewnej firmy za styczeń 2023 roku.
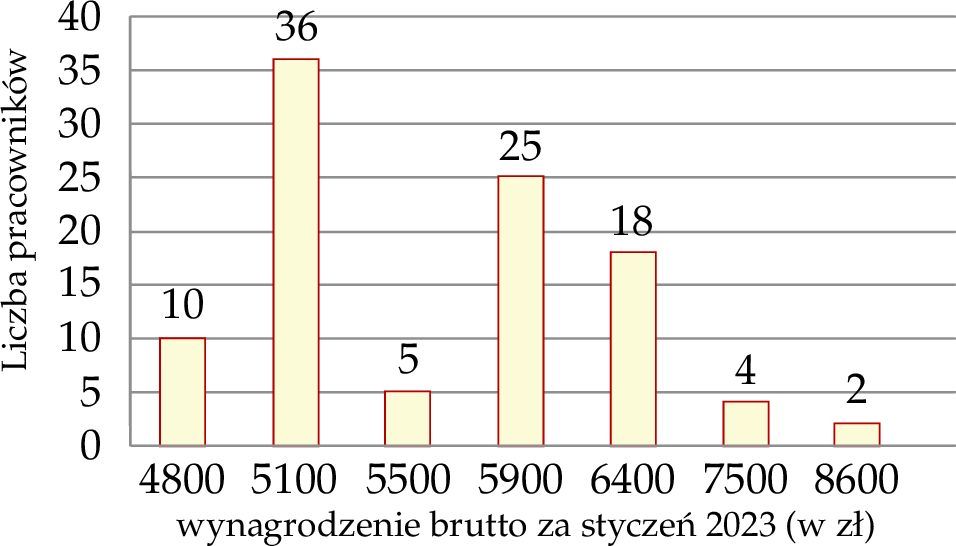
Średnia wynagrodzenia brutto wszystkich pracowników tej firmy za styczeń 2023 roku jest równa
A) 5 690 zł B) 5 280 zł C) 6 257 zł D) 5 900 zł
Zakład stolarski produkuje krzesła, które sprzedaje po 196 złotych za sztukę. Właściciel, na podstawie analizy rzeczywistych wpływów i wydatków, stwierdził, że:
-
przychód
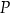 (w złotych) ze sprzedaży
(w złotych) ze sprzedaży  krzeseł można opisać funkcją
krzeseł można opisać funkcją 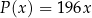
-
koszt
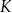 (w złotych) produkcji
(w złotych) produkcji  krzeseł dziennie można opisać funkcją
krzeseł dziennie można opisać funkcją 
Dziennie w zakładzie można wyprodukować co najwyżej 30 krzeseł. Oblicz, ile krzeseł powinien dziennie sprzedawać zakład, aby zysk ze sprzedaży krzeseł wyprodukowanych przez ten zakład w ciągu jednego dnia był możliwie największy. Oblicz ten największy zysk.