/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom rozszerzony 2 marca 2017 Czas pracy: 180 minut
Zadania zamknięte
Reszta z dzielenia wielomianu 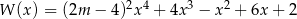 przez dwumian
przez dwumian 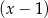 jest równa 11 dla
jest równa 11 dla
A) 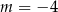 B)
B) 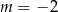 C)
C) 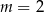 D)
D) 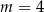
Dana jest funkcja 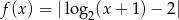 . Wykres tej funkcji jest przedstawiony na rysunku
. Wykres tej funkcji jest przedstawiony na rysunku
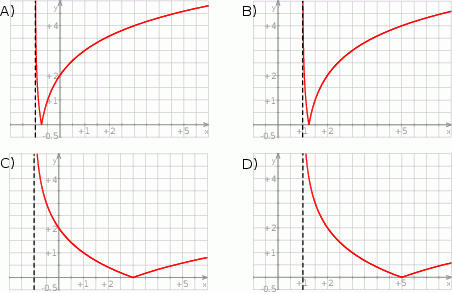
Wierzchołek 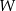 paraboli, będącej wykresem funkcji
paraboli, będącej wykresem funkcji 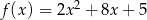 przesunięto o wektor
przesunięto o wektor 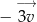 , gdzie
, gdzie ![→ v = [− 4;5]](https://img.zadania.info/zes/0071032/HzesT11x.gif) , otrzymując punkt
, otrzymując punkt 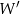 . Współrzędne punktu
. Współrzędne punktu 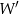 są równe
są równe
A) 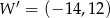 B)
B) 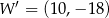 C)
C) 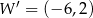 D)
D) 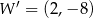
Szereg geometryczny:
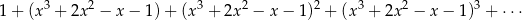
jest zbieżny dla
A) 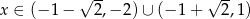
B) 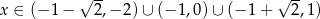
C) 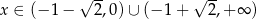
D) 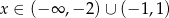
Styczna do wykresu funkcji 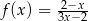 w punkcie o współrzędnych
w punkcie o współrzędnych 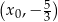 ma równanie
ma równanie
A) 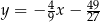 B)
B) 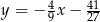 C)
C) 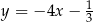 D)
D) 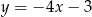
Zadania otwarte
Oblicz odległość środka okręgu 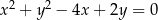 od prostej
od prostej 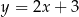 .
.
Na okręgu o promieniu  opisano trapez równoramienny, którego kąt ostry ma miarę
opisano trapez równoramienny, którego kąt ostry ma miarę  . Wykaż, że promień okręgu opisanego na tym czworokącie jest równy
. Wykaż, że promień okręgu opisanego na tym czworokącie jest równy 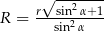 .
.
Widząc, że 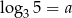 i
i 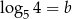 oblicz
oblicz 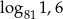 .
.
W klasie IIIA jest 12 dziewcząt i 14 chłopców, natomiast w klasie IIIB jest 10 dziewcząt i 16 chłopców. Rzucamy cztery razy sześcienną kostką do gry. Jeśli suma wyrzuconych oczek jest liczbą parzystą i co najmniej na jednej kostce wypadła parzysta liczba oczek, to wybieramy trzyosobową delegację z klasy IIIA, w przeciwnym wypadku z klasy IIIB. Oblicz prawdopodobieństwo, że w skład delegacji wejdzie co najmniej jeden chłopiec.
Dla jakich wartości parametru 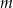 granica funkcji
granica funkcji 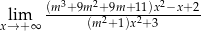 jest równa czwartemu wyrazowi ciągu określonego wzorem rekurencyjnym
jest równa czwartemu wyrazowi ciągu określonego wzorem rekurencyjnym 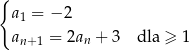
Oblicz, ile jest wszystkich liczb dziewięciocyfrowych, w zapisie których dokładnie trzy razy występuje siódemka, dokładnie dwa razy czwórka, a pozostałe cyfry nie mogą się powtarzać i żadna cyfra nie jest zerem.
Wykaż, że dla dowolnych nieujemnych liczb rzeczywistych  ,
, 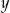 spełniona jest nierówność:
spełniona jest nierówność: 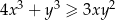 .
.
Rozwiąż równanie 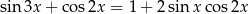 dla
dla 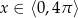 .
.
W ostrosłupie prawidłowym czworokątnym cosinus kąta między krawędziami bocznymi, które nie są sąsiednie jest równy 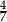 , a pole koła opisanego na podstawie ostrosłupa jest równe
, a pole koła opisanego na podstawie ostrosłupa jest równe 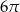 . Oblicz cosinus kąta
. Oblicz cosinus kąta  między sąsiednimi ścianami bocznymi ostrosłupa.
między sąsiednimi ścianami bocznymi ostrosłupa.
Środki okręgów 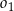 i
i 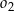 znajdują się po różnych stronach prostej
znajdują się po różnych stronach prostej 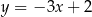 , która zawiera punkty wspólne tych okręgów. Wiedząc, że promień okręgu
, która zawiera punkty wspólne tych okręgów. Wiedząc, że promień okręgu 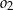 jest równy
jest równy 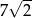 oraz, że okrąg
oraz, że okrąg 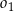 ma równanie
ma równanie 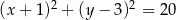 , wyznacz równanie okręgu
, wyznacz równanie okręgu 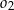 .
.
Tworząca stożka ma długość 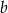 . Wyznacz wysokość tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.
. Wyznacz wysokość tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.
Wyznacz te wartości parametru 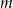 , dla których równanie
, dla których równanie
![(x− 3)[x 2 − 2(2m + 1 )x+ (m + 2)2] = 0](https://img.zadania.info/zes/0071032/HzesT58x.gif)
ma trzy różne rozwiązania.

