/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy
(technikum) 14 marca 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 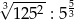 jest równa
jest równa
A) 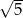 B)
B) 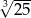 C)
C) 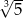 D) 5
D) 5
Liczby  i
i 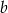 są dodatnie oraz 12% liczby
są dodatnie oraz 12% liczby  jest równe 15% liczby
jest równe 15% liczby 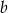 . Stąd wynika, że
. Stąd wynika, że  jest równe
jest równe
A) 103% liczby 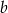 B) 125% liczby
B) 125% liczby 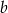 C) 150% liczby
C) 150% liczby 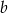 D) 153% liczby
D) 153% liczby 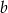
Wyrażenie 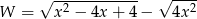 dla
dla 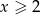 przyjmuje postać
przyjmuje postać
A) 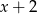 B)
B) 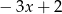 C)
C) 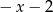 D)
D) 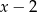
Suma dwudziestu początkowych wyrazów ciągu arytmetycznego 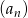 danego wzorem
danego wzorem 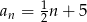 jest równa
jest równa
A) 205 B) 410 C) 200 D) 210
Jaką liczbę należy podstawić zamiast litery  , aby równanie
, aby równanie 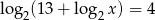 było prawdziwe?
było prawdziwe?
A) 8 B) 12 C) 16 D) 32
Wskaż liczbę, która spełnia równanie 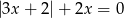 .
.
A) 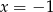 B)
B) 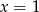 C)
C) 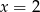 D)
D) 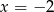
Najmniejsza wartość funkcji 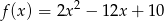 w przedziale
w przedziale 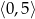 jest równa
jest równa
A) -1 B) -8 C) -10 D) 0
Rysunek przedstawia wykres funkcji 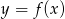 .
.
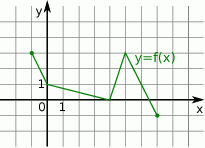
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 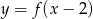 .
.
Która z podanych prostych jest styczna do okręgu 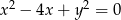 ?
?
A) 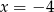 B)
B) 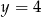 C)
C) 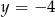 D)
D) 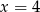
Funkcja liniowa 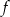 jest określona wzorem
jest określona wzorem 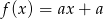 , gdzie
, gdzie 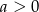 . Wówczas spełniony jest warunek
. Wówczas spełniony jest warunek
A) 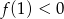 B)
B) 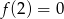 C)
C) 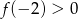 D)
D) 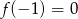
Wskaż nierówność, którą spełnia liczba 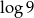 .
.
A) 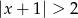 B)
B) 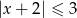 C)
C) 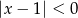 D)
D) 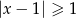
Z trójkąta 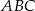 o obwodzie 50 wycięto kwadrat
o obwodzie 50 wycięto kwadrat 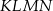 o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
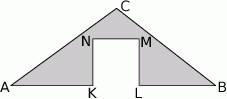
A) 65 B) 60 C) 75 D) 70
Wskaż przedział, który jest zbiorem rozwiązań nierówności 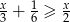
A) 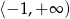 B)
B) 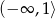 C)
C) 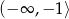 D)
D) 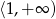
Dwa kolejne wyrazy ciągu geometrycznego 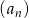 są równe 3 i 18. Wyrazem tego ciągu może być liczba
są równe 3 i 18. Wyrazem tego ciągu może być liczba
A) 27 B) 54 C) 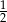 D)
D) 
Kąt  jest ostry i
jest ostry i 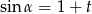 . Wtedy
. Wtedy
A) 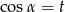 B)
B) 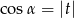 C)
C) 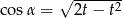 D)
D) 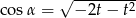
Promień okręgu wpisanego w trójkąt równoboczny jest o 2 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 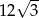 B)
B) 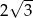 C)
C) 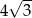 D)
D) 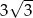
Przekrój osiowy walca jest kwadratem o boku  . Jeżeli
. Jeżeli 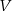 oznacza objętość walca,
oznacza objętość walca, 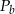 oznacza pole powierzchni bocznej walca, to
oznacza pole powierzchni bocznej walca, to
A) 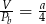 B)
B) 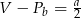 C)
C) 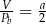 D)
D) 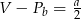
Która z liczb nie może być równa polu rombu o obwodzie 12?
A) 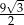 B)
B) 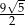 C)
C) 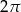 D)
D) 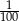
Punkty  i
i  leżą na okręgu o środku
leżą na okręgu o środku  (zobacz rysunek).
(zobacz rysunek).
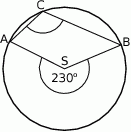
Miara zaznaczonego kąta wpisanego 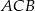 jest równa
jest równa
A) 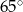 B)
B) 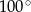 C)
C) 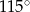 D)
D) 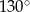
Liczba przekątnych sześcianu to
A) 6 B) 12 C) 8 D) 4
Pan Jakub ma 4 marynarki, 7 par różnych spodni i 10 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 280 B) 21 C) 28 D) 70
Zadania otwarte
Wyznacz najmniejszą wartość funkcji 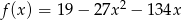 na przedziale
na przedziale 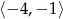 .
.
Proste o równaniach 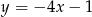 i
i 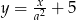 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
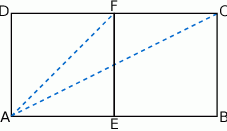
Odcinek 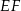 łączący środki dwóch dłuższych boków prostokąta
łączący środki dwóch dłuższych boków prostokąta  dzieli go na dwa kwadraty, przy czym przekątna prostokąta jest o 3 dłuższa od przekątnej kwadratu. Oblicz pole prostokąta
dzieli go na dwa kwadraty, przy czym przekątna prostokąta jest o 3 dłuższa od przekątnej kwadratu. Oblicz pole prostokąta  .
.
Ze zbioru 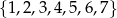 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 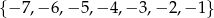 liczbę
liczbę 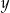 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 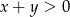 .
.
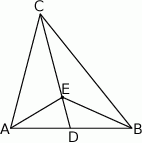
Na środkowej 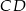 trójkąta
trójkąta 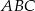 wybrano punkt
wybrano punkt 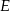 . Wykaż, że trójkąty
. Wykaż, że trójkąty 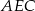 i
i 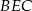 mają równe pola.
mają równe pola.
Wyznacz współrzędne punktu  , który dzieli odcinek o końcach
, który dzieli odcinek o końcach 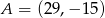 i
i 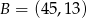 w stosunku
w stosunku 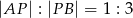 .
.
Udowodnij, że jeżeli 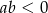 to
to 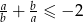 .
.
Oblicz pole rombu, w którym długość boku jest równa 13 cm, a długości przekątnych różnią się o 14 cm.
W trójkącie prostokątnym 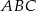 o przeciwprostokątnej
o przeciwprostokątnej 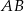 dane są wierzchołki
dane są wierzchołki 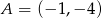 i
i 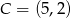 . Punkt
. Punkt 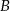 leży na prostej o równaniu
leży na prostej o równaniu 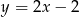 . Wyznacz równanie okręgu opisanego na tym trójkącie.
. Wyznacz równanie okręgu opisanego na tym trójkącie.
Mamy dwa pojemniki: pierwszy ma kształt sześcianu, drugi - ostrosłupa prawidłowego czworokątnego. Przekątna sześcianu ma długość 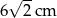 . Wysokość ostrosłupa tworzy ze ścianą boczną kąt o mierze
. Wysokość ostrosłupa tworzy ze ścianą boczną kąt o mierze 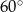 . Pole powierzchni bocznej ostrosłupa jest równe
. Pole powierzchni bocznej ostrosłupa jest równe 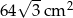 . Sprawdź na podstawie odpowiednich obliczeń, czy woda wypełniająca całkowicie pierwszy pojemnik zmieści się w drugim pojemniku.
. Sprawdź na podstawie odpowiednich obliczeń, czy woda wypełniająca całkowicie pierwszy pojemnik zmieści się w drugim pojemniku.

