/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas trzecich)
poziom podstawowy grupa II 12 stycznia 2011 Czas pracy: 170 minut
Zadania zamknięte
Liczba 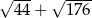 jest równa
jest równa
A) 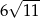 B)
B) 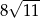 C)
C) 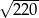 D)
D) 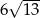
Liczba 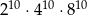 jest równa
jest równa
A) 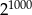 B)
B) 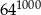 C)
C) 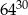 D)
D) 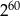
Rozwiązaniem równania 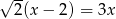 jest liczba
jest liczba
A) 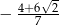 B)
B) 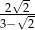 C)
C) 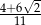 D)
D) 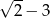
Suma wyrażeń 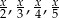 jest równa
jest równa
A) 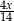 B)
B) 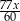 C)
C) 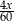 D)
D) 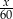
Pierwiastkami równania 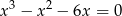 są liczby
są liczby
A) 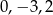 B)
B) 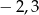 C)
C) 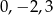 D)
D) 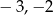
Jeżeli suma kątów wewnętrznych wielokąta foremnego jest równa 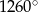 to wielokąt ten ma wierzchołków:
to wielokąt ten ma wierzchołków:
A) 8 B) 9 C) 7 D) 10
Jeżeli 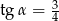 to to stosunek
to to stosunek 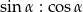 jest równy:
jest równy:
A) 3:4 B) 4:3 C) 1:1 D) 2:3
W trójkącie równoramiennym o bokach długości: 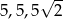 kąt przy podstawie ma miarę:
kąt przy podstawie ma miarę:
A) 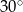 B)
B) 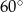 C)
C) 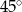 D)
D) 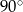
Punkt przecięcia środkowych w trójkącie 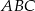 , gdzie
, gdzie 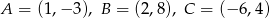 ma współrzędne:
ma współrzędne:
A) 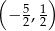 B)
B) 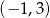 C)
C) 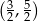 D)
D) 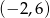
Liczby 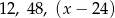 są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas trzeci wyraz tego ciągu jest równy:
są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas trzeci wyraz tego ciągu jest równy:
A) 24 B) 216 C) 60 D) 192
Przekątna kwadratu 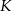 ma długość 2, a obwód kwadratu
ma długość 2, a obwód kwadratu 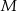 ma długość 16. Skala podobieństwa kwadratu
ma długość 16. Skala podobieństwa kwadratu 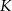 do kwadratu
do kwadratu 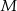 jest równa:
jest równa:
A) 4 B) 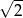 C)
C) 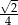 D)
D) 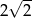
Przekrój osiowy walca jest kwadratem o boku długości 8. Pole powierzchni bocznej tego walca jest równe:
A) 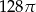 B)
B) 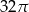 C)
C) 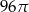 D)
D) 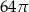
Funkcja 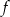 przyporządkowuje każdej liczbie naturalnej liczbę jej dzielników będących liczbami naturalnymi. Wobec tego
przyporządkowuje każdej liczbie naturalnej liczbę jej dzielników będących liczbami naturalnymi. Wobec tego 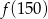 jest równe:
jest równe:
A) 11 B) 10 C) 13 D) 12
Dana jest funkcja kwadratowa 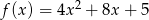 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 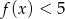 jest
jest
A) 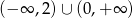 B)
B) 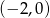 C)
C) 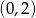 D)
D) 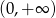
Liczba  stanowi 80% liczby dodatniej
stanowi 80% liczby dodatniej 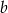 . O ile procent liczba
. O ile procent liczba 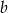 jest większa od liczby
jest większa od liczby  ?
?
A) 20% B) 80% C) 25% D) 120%
Liczba 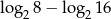 jest równa
jest równa
A) 2 B) 1 C) -1 D) 2
Osią symetrii wykresu funkcji 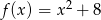 jest prosta o równaniu
jest prosta o równaniu
A) 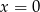 B)
B) 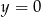 C)
C) 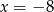 D)
D) 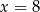
Pewnego dnia w klasie liczącej 11 dziewcząt i 15 chłopców nieobecny był jeden chłopiec i jedna dziewczynka. Nauczyciel wybrał do odpowiedzi jednego ucznia. Prawdopodobieństwo, że będzie to dziewczynka jest równe:
A) 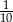 B)
B) 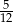 C)
C) 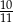 D)
D) 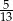
Miejscem zerowym funkcji 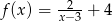 jest
jest
A) 3 B) 2,5 C) 2 D) -3
Wartość wyrażenia 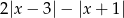 dla
dla 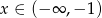 jest równa
jest równa
A) 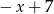 B)
B) 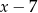 C)
C) 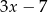 D)
D) 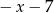
Kąt  jest ostry i
jest ostry i 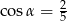 . Wówczas
. Wówczas
A) 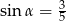 B)
B) 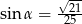 C)
C) 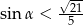 D)
D) 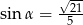
Prosta 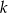 ma równanie
ma równanie 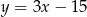 . Wskaż równanie prostej prostopadłej do
. Wskaż równanie prostej prostopadłej do 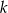 .
.
A) 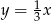 B)
B) 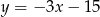 C)
C) 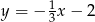 D)
D) 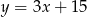
Trójkąt równoboczny o boku długości 4 cm obrócono wokół prostej zawierającej wysokość trójkąta. Objętość powstałej bryły jest równa:
A) 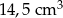 B)
B) 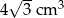 C)
C) 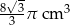 D)
D) 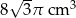
Zbiór 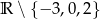 jest dziedziną wyrażenia:
jest dziedziną wyrażenia:
A) 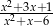 B)
B) 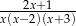 C)
C) 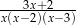 D)
D) 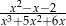
Ile jest liczb całkowitych wśród rozwiązań nierówności 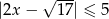 ?
?
A) 6 B) 4 C) 5 D) 7
Zadania otwarte
Rozwiąż równanie 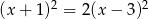 .
.
Rozwiąż równanie 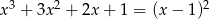 .
.
Podaj współrzędne punktu przecięcia się wykresu funkcji 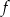 z osią
z osią 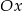 , gdy funkcja
, gdy funkcja 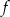 określona jest wzorem
określona jest wzorem
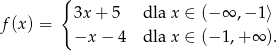
Uzasadnij, że istnieje jedna para 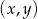 liczb całkowitych
liczb całkowitych 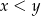 , których suma jest równa 23, a ich iloczyn jest równy 132.
, których suma jest równa 23, a ich iloczyn jest równy 132.
Sprawdź, czy prosta 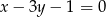 jest styczna do okręgu
jest styczna do okręgu 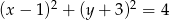 .
.
W trójkącie prostokątnym suma sinusów kątów ostrych jest równa  . Wykaż, że iloczyn cosinusów tych kątów jest równy
. Wykaż, że iloczyn cosinusów tych kątów jest równy 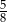 .
.
Na trójkącie równobocznym opisano drugi trójkąt równoboczny tak, że wierzchołki pierwszego trójkąta leżą na bokach drugiego. Boki obydwu trójkątów tworzą kąty 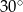 . Jakim procentem pola małego trójkąta jest pole dużego trójkąta?
. Jakim procentem pola małego trójkąta jest pole dużego trójkąta?
Koszt wynajęcia autokaru na wycieczkę klasową wynosił 1500 zł. Pięciu uczniów nie pojechało na wycieczkę i wtedy każdy z pozostałych uczniów musiał zapłacić o 10 zł więcej. Oblicz, ilu uczniów jest w tej klasie.
Oblicz cosinus kąta między krawędzią boczną i krawędzią podstawy ostrosłupa prawidłowego trójkątnego, jeżeli wiadomo, że promień okręgu opisanego na podstawie, wysokość ostrosłupa i krawędź boczna tworzą trójkąt równoramienny.

