/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 12 marca 2011 Czas pracy: 180 minut
Wykres funkcji homograficznej 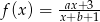 można otrzymać przesuwając wykres funkcji
można otrzymać przesuwając wykres funkcji 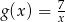 , a dziedzina funkcji
, a dziedzina funkcji 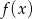 jest tym samym zbiorem co jej zbiór wartości. Wyznacz współczynniki
jest tym samym zbiorem co jej zbiór wartości. Wyznacz współczynniki  i
i 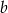 .
.
Długości boków prostokąta 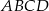 spełniają warunki:
spełniają warunki: 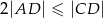 i
i 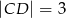 . Na boku
. Na boku 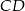 wybrano punkty
wybrano punkty 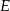 i
i 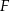 w ten sposób, że
w ten sposób, że 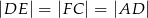 . Punkt
. Punkt 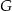 jest takim punktem odcinka
jest takim punktem odcinka 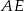 , że
, że 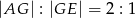 . Oblicz długość boku
. Oblicz długość boku 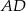 prostokąta, dla której pole trójkąta
prostokąta, dla której pole trójkąta 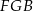 jest największe.
jest największe.
Rozwiąż równanie 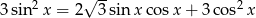 w przedziale
w przedziale 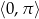 .
.
W trójkącie równoramiennym 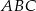 , gdzie
, gdzie 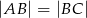 , podstawa ma długość 6. Punkt
, podstawa ma długość 6. Punkt 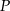 jest punktem przecięcia wysokości wychodzących z wierzchołków
jest punktem przecięcia wysokości wychodzących z wierzchołków 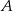 i
i 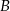 . Oblicz pole tego trójkąta, jeśli
. Oblicz pole tego trójkąta, jeśli 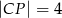 .
.
Ciągi 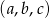 i
i 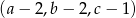 są ciągami geometrycznymi o wyrazach dodatnich, a ciąg
są ciągami geometrycznymi o wyrazach dodatnich, a ciąg 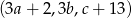 jest ciągiem arytmetycznym. Wyznacz
jest ciągiem arytmetycznym. Wyznacz 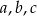 .
.
Udowodnij, że suma długości wysokości ścian bocznych ostrosłupa pięciokątnego jest nie większa niż suma długości jego krawędzi bocznych.
Wyznacz wszystkie wartości parametru 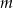 , dla których równanie
, dla których równanie 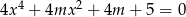 ma cztery różne pierwiastki rzeczywiste spełniające warunek
ma cztery różne pierwiastki rzeczywiste spełniające warunek
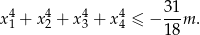
O zdarzeniach losowych 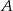 i
i 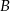 wiadomo, że
wiadomo, że 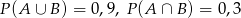 i
i 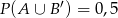 . Oblicz
. Oblicz 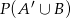 .
.
Punkt 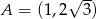 jest wierzchołkiem trójkąta równobocznego
jest wierzchołkiem trójkąta równobocznego 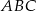 . Bok
. Bok 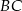 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 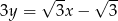 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 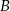 i
i 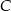 trójkąta.
trójkąta.
Trzy wychodzące z jednego wierzchołka krawędzie równoległościanu są równe 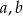 i
i  . Krawędzie
. Krawędzie  i
i 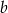 są prostopadłe, a krawędź
są prostopadłe, a krawędź  tworzy z każdą z nich kąt ostry
tworzy z każdą z nich kąt ostry  . Oblicz objętość równoległościanu.
. Oblicz objętość równoległościanu.

