/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (OKE Poznań)
poziom rozszerzony 11 stycznia 2010 Czas pracy: 180 minut
Udowodnij, że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.
Dla każdego 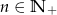 wyrazy ciągu
wyrazy ciągu 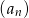 spełniają dwa warunki
spełniają dwa warunki 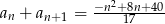 i
i 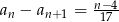 . Oblicz, które wyrazy tego ciągu są dodatnie.
. Oblicz, które wyrazy tego ciągu są dodatnie.
Liczbę 255 przedstaw jako sumę czterech całkowitych składników będących kolejnymi wyrazami ciągu geometrycznego tak, aby trzeci wyraz był o 45 większy od wyrazu pierwszego.
Różnymi pierwiastkami równania kwadratowego 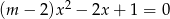 są liczby
są liczby 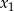 oraz
oraz 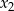 . Narysuj wykres funkcji
. Narysuj wykres funkcji 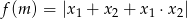 .
.
Wykaż, że w trójkącie prostokątnym suma długości obu przyprostokątnych jest równa sumie długości średnic okręgów wpisanego i opisanego na tym trójkącie.
Podstawą graniastosłupa prostego jest romb, którego krótsza przekątna ma długość  , a kąt ostry miarę
, a kąt ostry miarę 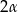 . Pole przekroju wyznaczonego przez krawędź boczną graniastosłupa i dłuższą przekątną podstawy wynosi
. Pole przekroju wyznaczonego przez krawędź boczną graniastosłupa i dłuższą przekątną podstawy wynosi 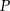 . Oblicz długość dłuższej przekątnej graniastosłupa, wykonaj rysunek bryły i zaznacz w nim właściwy przekrój.
. Oblicz długość dłuższej przekątnej graniastosłupa, wykonaj rysunek bryły i zaznacz w nim właściwy przekrój.
W czworokącie 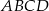 przekątne przecinają się w punkcie o współrzędnych
przekątne przecinają się w punkcie o współrzędnych 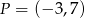 w taki sposób, że
w taki sposób, że 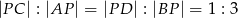 . Wiedząc, że
. Wiedząc, że ![−→ AC = [4 ,6]](https://img.zadania.info/zes/0074152/HzesT14x.gif) i
i ![− → BD = [−1 0,− 2]](https://img.zadania.info/zes/0074152/HzesT15x.gif) , oblicz współrzędne wierzchołków tego czworokąta. Uzasadnij, że czworokąt
, oblicz współrzędne wierzchołków tego czworokąta. Uzasadnij, że czworokąt 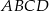 jest trapezem.
jest trapezem.
Wykaż, że cosinus kąta przecięcia się wykresów funkcji 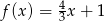 i
i 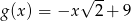 jest równy
jest równy 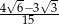 .
.
Oblicz wartość funkcji 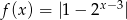 dla argumentu
dla argumentu
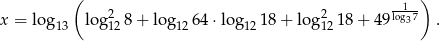
Posługując się wykresem funkcji 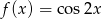 dla
dla 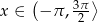 , rozwiąż nierówność
, rozwiąż nierówność 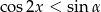 wiedząc, że miara kąta
wiedząc, że miara kąta  jest równa mierze łukowej kąta środkowego okręgu opartego na
jest równa mierze łukowej kąta środkowego okręgu opartego na 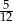 okręgu.
okręgu.
Liczba uczniów w klasie jest 812 razy mniejsza od liczby utworzonych z nich uporządkowanych trójek. Oblicz prawdopodobieństwo wylosowania trzech osób, które (w kolejności losowania) są zapisane w dzienniku pod numerami pierwszym, drugim, i trzecim.

