/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom podstawowy grupa I 23 maja 2017 Czas pracy: 170 minut
Zadania zamknięte
Jeżeli 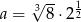 i
i 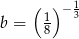 , to wartość wyrażenia
, to wartość wyrażenia 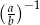 jest równa
jest równa
A) 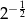 B)
B) 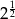 C)
C) 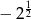 D)
D) 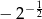
Jeżeli liczba 91 jest o 40% większa od liczby  , to liczba
, to liczba  jest równa
jest równa
A) 72 B) 70 C) 68 D) 65
Wartość wyrażenia 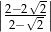 jest równa
jest równa
A) 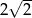 B)
B) 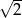 C)
C) 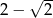 D) 2
D) 2
Jeśli 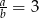 , to wartość wyrażenia
, to wartość wyrażenia 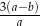 jest równa
jest równa
A) 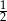 B)
B)  C) 2 D) 3
C) 2 D) 3
Wartość wyrażenia 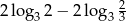 jest równa
jest równa
A) 4 B) 2 C) 3 D) 1
Funkcja kwadratowa 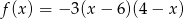 jest malejąca w przedziale
jest malejąca w przedziale
A) 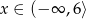 B)
B) 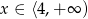 C)
C) 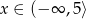 D)
D) 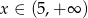
Wartość wyrażenia 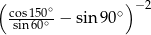 jest równa
jest równa
A) 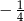 B)
B) 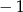 C) 1 D)
C) 1 D) 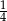
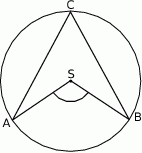
Punkt 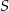 jest środkiem okręgu, na którym leżą punkty
jest środkiem okręgu, na którym leżą punkty 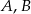 i
i 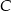 (patrz rysunek). Jeśli
(patrz rysunek). Jeśli 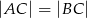 i miara kąta wypukłego
i miara kąta wypukłego 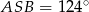 , to kąt wypukły
, to kąt wypukły 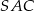 jest równy
jest równy
A) 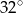 B)
B) 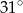 C)
C) 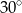 D)
D) 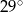
Miary kątów trójkąta tworzą ciąg geometryczny o ilorazie 4. Miara największego z nich jest równa
A) 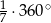 B)
B) 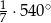 C)
C) 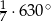 D)
D) 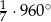
Dziedziną funkcji 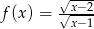 jest przedział
jest przedział
A) 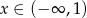 B)
B) 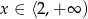 C)
C) 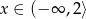 D)
D) 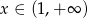
Pole powierzchni trójkąta równoramiennego o ramionach długości 6 cm i kącie między nimi 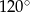 jest równe
jest równe
A) 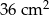 B)
B) 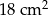 C)
C) 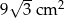 D)
D) 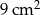
Jeżeli 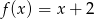 i
i 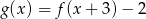 , to funkcja
, to funkcja 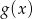 jest równa
jest równa
A) 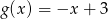 B)
B) 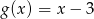 C)
C) 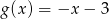 D)
D) 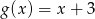
Dziedziną funkcji 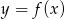 jest przedział
jest przedział 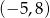 . Zatem dziedziną funkcji
. Zatem dziedziną funkcji 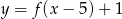 jest przedział
jest przedział
A) 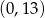 B)
B) 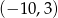 C)
C) 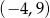 D)
D) 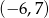
Punkt 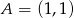 jest jednym z wierzchołków kwadratu
jest jednym z wierzchołków kwadratu 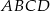 , a punkt
, a punkt 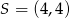 jest środkiem okręgu wpisanego w ten kwadrat. Przekątna tego kwadratu ma długość
jest środkiem okręgu wpisanego w ten kwadrat. Przekątna tego kwadratu ma długość
A) 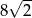 B)
B) 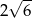 C)
C) 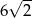 D)
D) 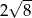
O funkcji liniowej 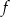 wiadomo, że
wiadomo, że 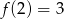 oraz punkt
oraz punkt 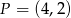 należy do jej wykresu. Wzór funkcji
należy do jej wykresu. Wzór funkcji 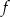 to
to
A) 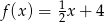 B)
B) 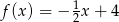 C)
C) 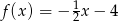 D)
D) 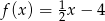
Długość odcinka zaznaczonego na rysunku literką  jest równa
jest równa
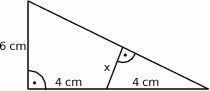
A) 2,4 cm B) 3 cm C) 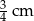 D) 2 cm
D) 2 cm
Zbiorem wartości funkcji 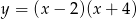 jest przedział
jest przedział
A) 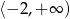 B)
B) 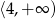 C)
C) 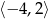 D)
D) 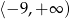
Dany jest trójwyrazowy ciąg arytmetyczny 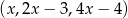 . Stąd wynika, że
. Stąd wynika, że  jest równy
jest równy
A) 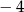 B)
B) 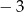 C)
C) 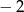 D)
D) 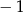
Wyrażenie 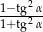 jest równe
jest równe
A) 1 B) 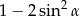 C) 0 D)
C) 0 D) 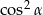
Dla każdej liczby całkowitej dodatniej  suma
suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 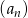 jest określona wzorem
jest określona wzorem 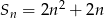 . Wtedy wyraz
. Wtedy wyraz 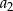 jest równy
jest równy
A) 4 B) 8 C) 12 D) 24
Najmniejszą liczbą całkowitą spełniającą nierówność 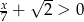 jest
jest
A) 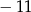 B)
B) 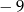 C)
C) 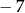 D) 9
D) 9
Liczby 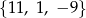 są trzema początkowymi wyrazami ciągu arytmetycznego
są trzema początkowymi wyrazami ciągu arytmetycznego 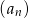 , określonego dla liczb naturalnych
, określonego dla liczb naturalnych 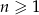 . Wzór ogólny tego ciągu ma postać
. Wzór ogólny tego ciągu ma postać
A) 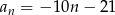 B)
B) 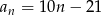 C)
C) 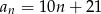 D)
D) 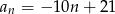
Trzeci wyraz malejącego ciągu geometrycznego jest równy 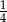 , a piąty
, a piąty 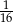 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 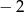 B)
B) 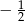 C)
C) 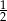 D) 2
D) 2
Punkt 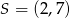 jest środkiem odcinka
jest środkiem odcinka 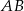 , w którym
, w którym 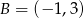 . Punkt
. Punkt 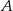 ma współrzędne:
ma współrzędne:
A) 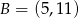 B)
B) 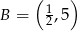 C)
C) 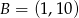 D)
D) 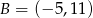
Do wykresu funkcji określonej wzorem 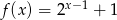 , należy punkt o współrzędnych
, należy punkt o współrzędnych
A) 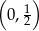 B)
B) 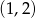 C)
C) 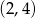 D)
D) 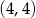
Zadania otwarte
Wyznacz zbiór całkowitych rozwiązań nierówności 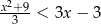 .
.
Wykaż, ze dla dowolnych liczb rzeczywistych 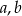 prawdziwa jest nierówność
prawdziwa jest nierówność 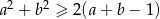 .
.
Ile wyrazów ujemnych ma ciąg 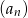 określony wzorem
określony wzorem 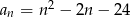 dla
dla 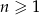 ?
?
Rozwiąż równanie 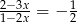 .
.
Kąt  jest ostry oraz
jest ostry oraz 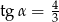 . Oblicz
. Oblicz 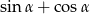 .
.
Oblicz długości boków trójkąta prostokątnego o polu powierzchni równym 20, wiedząc, że długości jego przyprostokątnych różnią się o 6.
W trójkącie prostokątnym 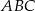 z wierzchołka kąta prostego poprowadzono odcinek
z wierzchołka kąta prostego poprowadzono odcinek 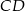 taki, że
taki, że 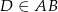 . Trójkąt
. Trójkąt 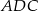 jest równoboczny. Oblicz pole trójkąta
jest równoboczny. Oblicz pole trójkąta 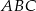 , wiedząc, że jego obwód jest równy 6.
, wiedząc, że jego obwód jest równy 6.
Szósty wyraz ciągu arytmetycznego 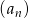 jest o 6 mniejszy od czwartego wyrazu. Wyznacz wzór ogólny na
jest o 6 mniejszy od czwartego wyrazu. Wyznacz wzór ogólny na  –ty wyraz ciągu
–ty wyraz ciągu 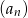 , wiedząc, że ciąg
, wiedząc, że ciąg 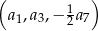 jest geometryczny.
jest geometryczny.
Dany jest trójkąt 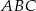 , gdzie
, gdzie 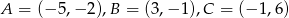 .
.
- Wyznacz równanie prostej zawierającej bok
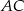 .
. - Oblicz długość środkowej
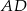 .
. - Wyznacz równanie prostej zawierającej wysokość poprowadzoną z wierzchołka
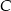 .
. - Oblicz pole tego trójkąta.

