/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy+ 9 kwietnia 2011 Czas pracy: 170 minut
Zadania zamknięte
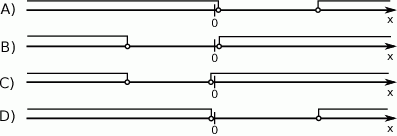
Wskaż rysunek, który może przedstawiać zbiór rozwiązań nierówności 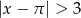 .
.
W solance, która zawierała 5% soli zwiększono zawartość soli o 500%. Stężenie soli w otrzymanym roztworze wynosi
A) 50% B) 30% C) 24% D) 25%
Jeżeli 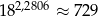 to przybliżona wartość liczby
to przybliżona wartość liczby 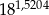 jest równa
jest równa
A) 81 B) 27 C) 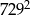 D) 19683
D) 19683
Jeżeli 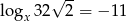 to liczba
to liczba  jest równa
jest równa
A) 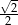 B)
B) 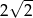 C)
C) 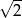 D) 2
D) 2
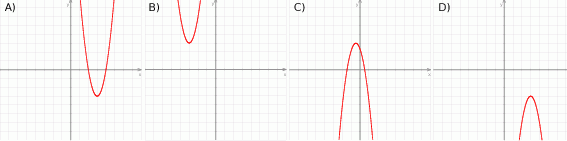
Który z rysunków może przedstawiać wykres funkcji kwadratowej 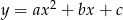 takiej, że
takiej, że 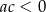 ?
?
Czwarta potęga liczby 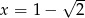 jest równa
jest równa
A) 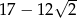 B)
B) 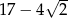 C)
C) 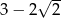 D)
D) 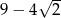
Do zbioru rozwiązań nierówności 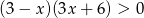 należy liczba
należy liczba
A) 3 B) 2 C) -2 D) -3
Liczby 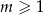 i
i 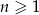 spełniają warunek
spełniają warunek 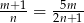 . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 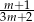 B)
B) 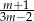 C)
C) 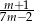 D)
D) 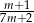
Korzystając z danego wykresu funkcji 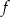 , wskaż nierówność prawdziwą
, wskaż nierówność prawdziwą
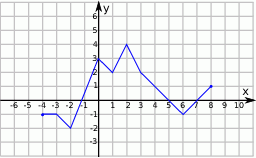
A) 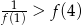 B)
B) ![[f (−3 )]2 < f (4)](https://img.zadania.info/zes/0074990/HzesT30x.gif) C)
C) 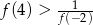 D)
D) ![2 f(3) > [f (3)]](https://img.zadania.info/zes/0074990/HzesT32x.gif)
Suma 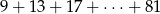 kolejnych wyrazów ciągu arytmetycznego jest równa
kolejnych wyrazów ciągu arytmetycznego jest równa
A) 859 B) 851 C) 855 D) 1710
Liczba 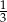 jest wartością wyrażenia
jest wartością wyrażenia
A) 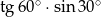 B)
B) 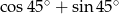 C)
C) 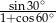 D)
D) 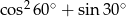
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 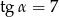 . Wówczas wartość wyrażenia
. Wówczas wartość wyrażenia 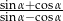 jest równa
jest równa
A) 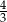 B)
B) 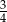 C)
C) 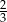 D)
D) 
W ciągu geometrycznym 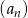 o wyrazach dodatnich spełnione są warunki:
o wyrazach dodatnich spełnione są warunki: 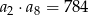 oraz
oraz 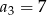 . Iloraz tego ciąg jest równy
. Iloraz tego ciąg jest równy
A) 4 B) 2 C) 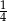 D)
D) 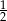
Wskaż 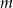 , dla którego proste
, dla którego proste 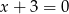 i
i 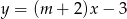 są prostopadłe.
są prostopadłe.
A) 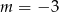 B)
B) 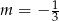 C)
C) 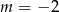 D)
D) 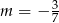
Okrąg o równaniu 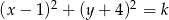 jest styczny do osi
jest styczny do osi 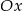 . Liczba
. Liczba 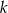 jest równa
jest równa
A) 2 B) 4 C) 8 D) 16
Ile jest liczb naturalnych trzycyfrowych, których kolejne cyfry tworzą ciąg geometryczny o ilorazie równym 2 lub 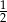 ?
?
A) 4 B) 16 C) 8 D) 9
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 2 | 4 | 3 | 4 | 5 | 3 |
Mediana tych danych jest równa.
A) 3 B) 3,5 C) 4 D) 5
Na rysunku zaznaczono długości niektórych odcinków w rombie oraz kąt  .
.
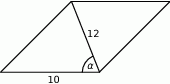
Wtedy
A) 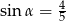 B)
B) 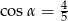 C)
C) 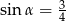 D)
D) 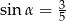
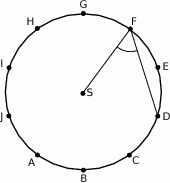
Punkty 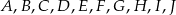 dzielą okrąg o środku
dzielą okrąg o środku 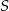 na dziesięć równych łuków. Oblicz miarę kąta
na dziesięć równych łuków. Oblicz miarę kąta 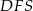 zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 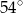 B)
B) 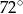 C)
C) 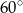 D)
D) 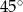
Podstawą prostopadłościanu jest prostokąt o wymiarach 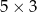 , a jego pole powierzchni całkowitej jest równe 94. Wysokość tego prostopadłościanu ma długość
, a jego pole powierzchni całkowitej jest równe 94. Wysokość tego prostopadłościanu ma długość
A) 2 B) 3 C) 4 D) 5
Zadania otwarte
Dane są funkcje 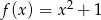 i
i 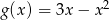 . Rozwiąż nierówność
. Rozwiąż nierówność 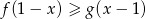 .
.
Rozwiąż równanie 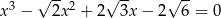 .
.
W trójkącie równobocznym 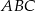 dane są wierzchołek
dane są wierzchołek 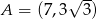 i środek okręgu wpisanego
i środek okręgu wpisanego 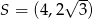 . Oblicz pole trójkąta
. Oblicz pole trójkąta 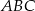 .
.
Wykaż, że jeżeli 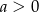 , to
, to 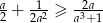 .
.
Wykaż, że jeżeli liczby 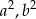 i
i 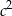 tworzą ciąg arytmetyczny, który nie jest stały, to liczby
tworzą ciąg arytmetyczny, który nie jest stały, to liczby 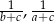 i
i 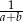 również tworzą ciąg arytmetyczny.
również tworzą ciąg arytmetyczny.
Wiedząc, że  , oblicz
, oblicz 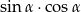 .
.
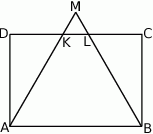
Dany jest prostokąt 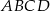 , w którym
, w którym 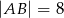 i
i 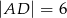 . Na boku
. Na boku 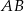 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 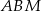 (patrz rysunek). Oblicz obwód trójkąta
(patrz rysunek). Oblicz obwód trójkąta 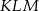 .
.
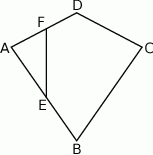
Punkty 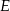 i
i 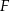 są środkami boków
są środkami boków 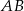 i
i 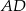 deltoidu
deltoidu 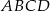 . Pole trójkąta
. Pole trójkąta 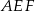 jest równe 3. Oblicz pole deltoidu
jest równe 3. Oblicz pole deltoidu 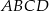 .
.
Suma sześcianów trzech kolejnych liczb całkowitych wynosi -36. Wyznacz te liczby.
Doświadczenie losowe polega na trzykrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 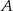 polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek otrzymanych w trzech rzutach będzie podzielny przez 48.
polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek otrzymanych w trzech rzutach będzie podzielny przez 48.
Parking wyłożono płytami betonowymi w kształcie prostokątów. Gdyby ten sam parking wyłożyć prostokątnymi płytami o powierzchni większej o 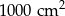 to liczba użytych płyt zmniejszyłaby się o 8. Gdyby natomiast użyć płyt o powierzchni mniejszej o
to liczba użytych płyt zmniejszyłaby się o 8. Gdyby natomiast użyć płyt o powierzchni mniejszej o 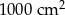 , to liczba użytych płyt zwiększyłaby się o 12. Oblicz pole powierzchni parkingu.
, to liczba użytych płyt zwiększyłaby się o 12. Oblicz pole powierzchni parkingu.

