/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (OKE Poznań)
poziom rozszerzony Styczeń 2008 Czas pracy: 180 minut
Wyznacz dziedzinę funkcji
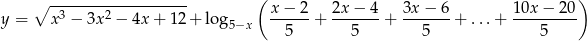
Rozwiąż równanie 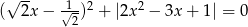 .
.
Dla jakiego parametru 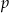 iloczyn miejsc zerowych funkcji
iloczyn miejsc zerowych funkcji 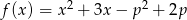 jest równy mniejszemu pierwiastkowi równania
jest równy mniejszemu pierwiastkowi równania 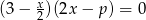 .
.
Sinus pewnego kąta ostrego  , liczba
, liczba  oraz cosinus tego samego kąta
oraz cosinus tego samego kąta  tworzą w podanej kolejności ciąg geometryczny. Oblicz sumę
tworzą w podanej kolejności ciąg geometryczny. Oblicz sumę 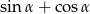 .
.
Różnica między drugim wyrazem ciągu geometrycznego a pierwszym wyrazem tego ciągu wynosi -6, a różnica między czwartym a pierwszym wyrazem tego ciągu jest równa -18. Oblicz trzeci wyraz tego ciągu.
Uzasadnij, że suma długości wysokości w dowolnym trójkącie jest mniejsza od jego obwodu.
Pole trapezu prostokątnego opisanego na okręgu jest równe 5, a obwód trapezu wynosi 10. Oblicz długość promienia okręgu.
Końcami odcinka są punkty o współrzędnych 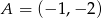 oraz
oraz 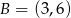 . Odcinek
. Odcinek 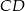 jest obrazem odcinka
jest obrazem odcinka 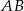 zarówno w jednokładności o dodatniej skali i środku
zarówno w jednokładności o dodatniej skali i środku 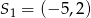 , jak i w jednokładności o ujemnej skali i środku
, jak i w jednokładności o ujemnej skali i środku 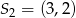 . Oblicz współrzędne końców odcinka
. Oblicz współrzędne końców odcinka 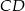 oraz skalę jednokładności o środku
oraz skalę jednokładności o środku 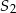 .
.
Spośród liczb 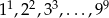 wybieramy losowo trzy. Oblicz prawdopodobieństwo, że iloczyn tych liczb jest parzysty.
wybieramy losowo trzy. Oblicz prawdopodobieństwo, że iloczyn tych liczb jest parzysty.
W trójkąt prostokątny o przyprostokątnych o długościach 2 i 4 wpisano prostokąt w ten sposób, że dwa jego boki leżą na przyprostokątnych trójkąta, a jeden z wierzchołków prostokąta leży na przeciwprostokątnej trójkąta. Prostokąt ten obraca się dookoła prostej, zawierającej dłuższą przyprostokątną trójkąta, tworząc walec. Oblicz, który z walców, otrzymanych w powyższy sposób, posiada największe pole powierzchni bocznej i oblicz jego objętość.

