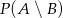/Szkoła średnia/Zadania maturalne
Przykładowe zadania
maturalne z matematyki Matura 2010 poziom podstawowy Informator CKE
1. Wykorzystanie i tworzenie informacji
Diagram przedstawia wyniki ankiety, w której ankietowani odpowiedzieli na pytanie, jakie napoje piją między posiłkami. Ankietowani wybierali tylko jeden z czterech rodzajów napojów.
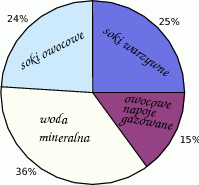
Na podstawie informacji przedstawionych na diagramie oblicz:
- ile procent badanych osób pije soki owocowe lub wodę mineralną,
- ile procent badanych osób nie pije owocowych napojów gazowanych,
- ile procent badanych osób nie pije soków warzywnych i nie pije wody mineralnej.
Dany jest ciąg 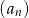 określony wzorem
określony wzorem 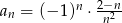 dla
dla 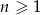 . Oblicz
. Oblicz 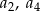 i
i 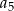 .
.
Przedstaw 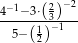 w postaci nieskracalnego ułamka zwykłego.
w postaci nieskracalnego ułamka zwykłego.
Podaj miejsca zerowe funkcji 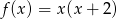 .
.
Oblicz 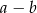 , gdy
, gdy 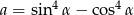 ,
, 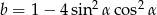 dla
dla 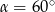 .
.
Wskaż równanie okręgu o środku w punkcie 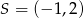 i promieniu
i promieniu 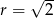 .
.
A) 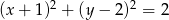
B) 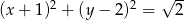
C) 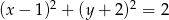
D) 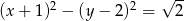
2. Wykorzystanie i interpretowanie reprezentacji
Na osi liczbowej zaznaczono przedział 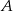 złożony z tych liczb rzeczywistych, których odległość od punktu 1 jest niewiększa od 4,5. Przedział
złożony z tych liczb rzeczywistych, których odległość od punktu 1 jest niewiększa od 4,5. Przedział 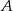 przesunięto wzdłuż osi o 2 jednostki w kierunku dodatnim, otrzymując przedział
przesunięto wzdłuż osi o 2 jednostki w kierunku dodatnim, otrzymując przedział 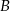 . Wyznacz wszystkie liczby całkowite, które należą jednocześnie do
. Wyznacz wszystkie liczby całkowite, które należą jednocześnie do 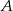 i do
i do 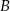 .
.
Rozwiąż równanie 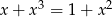 .
.
Oblicz największą i najmniejszą wartość funkcji 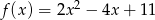 w przedziale
w przedziale 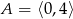 .
.
Pan Kowalski planując wyjazd na wakacje letnie w następnym roku postanowił założyć lokatę, wpłacając do banku 2000 zł na okres jednego roku. Ma do wyboru trzy rodzaje lokat: lokata 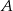 – oprocentowanie w stosunku rocznym 5%, kapitalizacja odsetek po roku;
– oprocentowanie w stosunku rocznym 5%, kapitalizacja odsetek po roku;
lokata 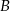 – oprocentowanie w stosunku rocznym 4,8%, kapitalizacja odsetek co pół roku;
– oprocentowanie w stosunku rocznym 4,8%, kapitalizacja odsetek co pół roku;
lokata 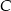 – oprocentowanie w stosunku rocznym 4,6%, kapitalizacja odsetek co kwartał.
– oprocentowanie w stosunku rocznym 4,6%, kapitalizacja odsetek co kwartał.
Oceń, wykonując odpowiednie obliczenia, która lokata jest najkorzystniejsza dla Pana Kowalskiego.
W trójkącie równoramiennym 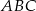 , w którym
, w którym 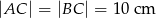 , wysokość poprowadzona z wierzchołka
, wysokość poprowadzona z wierzchołka 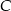 jest równa 5 cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w stopniach.
jest równa 5 cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w stopniach.
Ostrokątny trójkąt równoramienny 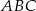 o podstawie
o podstawie 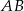 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 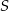 , przy czym kąt
, przy czym kąt 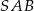 ma miarę
ma miarę 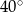 . Oblicz miarę kąta
. Oblicz miarę kąta 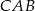 .
.
Oblicz odległość punktu 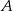 od środka odcinka
od środka odcinka 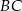 , gdzie
, gdzie 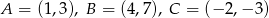 .
.
W graniastosłupie czworokątnym prawidłowym przekątna o długości 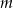 jest nachylona do płaszczyzny podstawy pod kątem
jest nachylona do płaszczyzny podstawy pod kątem  . Wiadomo, że
. Wiadomo, że 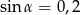 . Wyznacz objętość tego graniastosłupa.
. Wyznacz objętość tego graniastosłupa.
O zdarzeniach losowych 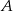 i
i 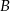 wiemy, że:
wiemy, że: 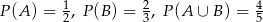 . Oblicz:
. Oblicz:
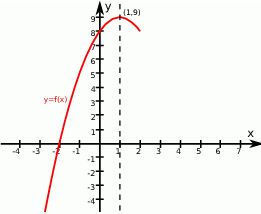
Na podstawie fragmentu wykresu funkcji kwadratowej 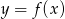 wskaż, które zdanie jest prawdziwe.
wskaż, które zdanie jest prawdziwe.
A) Miejscami zerowymi funkcji są liczby: -2 oraz 4.
B) Funkcja jest rosnąca w przedziale 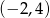 .
.
C) Funkcja przyjmuje wartości większe od zera dla 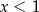 .
.
D) Zbiorem wartości funkcji jest przedział 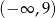 .
.
W kolejce do kasy biletowej ustawiły się cztery dziewczynki i pięciu chłopców. Liczba wszystkich możliwych ustawień osób w tej kolejce wynosi
A) 4!+5! B) 9! C) 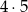 D)
D) 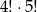
3. Modelowanie matematyczne
Dany jest prostokąt o bokach  i
i 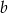 . Zmniejszamy długość boku
. Zmniejszamy długość boku  o 10% oraz zwiększamy długość boku
o 10% oraz zwiększamy długość boku 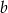 o 20%.
o 20%.
- O ile procent zwiększy się pole tego prostokąta?
- Wyznacz długość boku
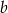 , dla której nowy prostokąt będzie miał taki sam obwód jak prostokąt wyjściowy, jeśli wiadomo, że bok
, dla której nowy prostokąt będzie miał taki sam obwód jak prostokąt wyjściowy, jeśli wiadomo, że bok  ma długość 30 cm.
ma długość 30 cm.
Liczbę 42 przedstaw w postaci sumy dwóch składników tak, by różnica ich kwadratów była równa 168.
Dla każdej liczby rzeczywistej 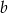 równanie
równanie 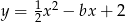 opisuje pewną parabolę. Wyznacz wszystkie wartości parametru
opisuje pewną parabolę. Wyznacz wszystkie wartości parametru 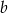 , dla których wierzchołek paraboli leży nad osią
, dla których wierzchołek paraboli leży nad osią 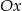 .
.
Punkt 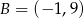 należy do okręgu stycznego do osi
należy do okręgu stycznego do osi 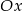 w punkcie
w punkcie 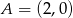 . Wyznacz równanie tego okręgu.
. Wyznacz równanie tego okręgu.
Strzelając do tarczy pewien strzelec uzyskuje co najmniej 9 punktów z prawdopodobieństwem 0,5, a co najwyżej 9 punktów z prawdopodobieństwem 0,7. Oblicz prawdopodobieństwo, że ten strzelec uzyska dokładnie 9 punktów.
Długość ramienia 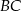 trapezu prostokątnego jest dwa razy większa od różnicy długości jego podstaw. Kąt
trapezu prostokątnego jest dwa razy większa od różnicy długości jego podstaw. Kąt 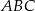 ma miarę
ma miarę
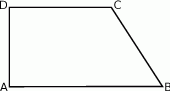
A) 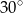 B)
B) 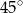 C)
C) 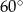 D)
D) 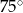
4. Użycie i tworzenie strategii
Podaj przykład liczb całkowitych dodatnich  i
i 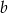 , spełniających nierówność
, spełniających nierówność 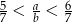 .
.
Stosując wzory skróconego mnożenia rozłóż na czynniki wyrażenie 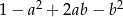 .
.
W ciągu arytmetycznym 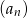 dane są wyrazy:
dane są wyrazy: 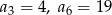 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości  , dla których wyrazy ciągu
, dla których wyrazy ciągu 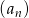 są mniejsze od 200.
są mniejsze od 200.
Liczby dodatnie 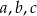 spełniają warunek:
spełniają warunek: 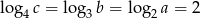 . Oblicz
. Oblicz 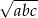 .
.
Ile punktów wspólnych ma okrąg o równaniu 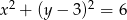 z prostą o równaniu
z prostą o równaniu 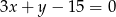 ?
?
Zbiorem wartości funkcji kwadratowej 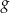 jest przedział
jest przedział 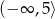 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 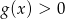 jest przedział
jest przedział 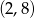 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 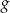 .
.
Rozwiąż równanie 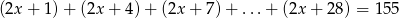 , jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
, jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 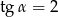 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 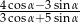 .
.
Dany jest trójkąt prostokątny 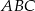 o przeciwprostokątnej
o przeciwprostokątnej 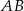 , taki że
, taki że 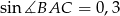 i
i 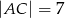 . Oblicz pole koła opisanego na tym trójkącie.
. Oblicz pole koła opisanego na tym trójkącie.
W układzie współrzędnych na płaszczyźnie zaznaczono punkty 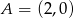 i
i 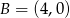 . Wyznacz wszystkie możliwe położenia punktu
. Wyznacz wszystkie możliwe położenia punktu 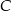 , dla których
, dla których 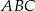 jest trójkątem równoramiennym o podstawie
jest trójkątem równoramiennym o podstawie 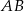 i polu równym 3.
i polu równym 3.
Rzucamy trzy razy symetryczną sześcienną kostką do gry. Opisz zbiór wszystkich zdarzeń elementarnych, a następnie oblicz prawdopodobieństwo, że w każdym rzucie liczba oczek będzie większa od numeru rzutu.
5. Rozumowanie i argumentacja
Wiadomo, że 1,5849 jest przybliżeniem liczby 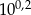 z zaokrągleniem do 4 miejsc po przecinku. Wyznacz przybliżenie liczby
z zaokrągleniem do 4 miejsc po przecinku. Wyznacz przybliżenie liczby 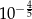 z zaokrągleniem do 3 miejsc po przecinku oraz przybliżenie liczby
z zaokrągleniem do 3 miejsc po przecinku oraz przybliżenie liczby 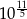 z zaokrągleniem do 1 miejsca po przecinku.
z zaokrągleniem do 1 miejsca po przecinku.
Wykaż, że dla 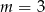 nierówność
nierówność 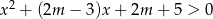 jest spełniona przez wszystkie liczby rzeczywiste
jest spełniona przez wszystkie liczby rzeczywiste  .
.
Jednym z miejsc zerowych funkcji kwadratowej 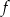 jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to
jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to 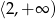 . Największa wartość funkcji
. Największa wartość funkcji 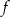 w przedziale
w przedziale 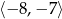 jest równa
jest równa 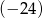 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 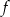 i narysuj jej wykres.
i narysuj jej wykres.
W pewnym trójkącie prostokątnym suma cosinusów kątów ostrych jest równa 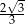 . Oblicz iloczyn sinusów tych kątów.
. Oblicz iloczyn sinusów tych kątów.
Dany jest trapez 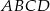 o podstawach
o podstawach 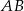 i
i 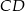 . Przekątne tego trapezu przecinają się w punkcie
. Przekątne tego trapezu przecinają się w punkcie 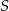 . Wykaż, że
. Wykaż, że 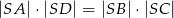 .
.
Prostokąt 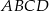 obracając się wokół boku
obracając się wokół boku 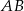 , zakreślił walec
, zakreślił walec 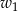 . Ten sam prostokąt obracając się wokół boku
. Ten sam prostokąt obracając się wokół boku 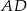 , zakreślił walec
, zakreślił walec 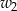 . Otrzymane walce mają równe pola powierzchni całkowitych. Wykaż, że prostokąt
. Otrzymane walce mają równe pola powierzchni całkowitych. Wykaż, że prostokąt 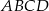 jest kwadratem.
jest kwadratem.