/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 18 marca 2017 Czas pracy: 180 minut
Zadania zamknięte
Styczna do wykresu funkcji 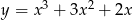 w punkcie
w punkcie 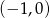 ma równanie
ma równanie
A) 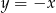 B)
B) 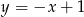 C)
C) 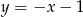 D)
D) 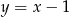
W trapezie 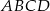 o podstawach
o podstawach 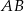 i
i 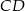 dane są:
dane są: 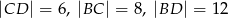 oraz
oraz 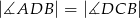 (zobacz rysunek).
(zobacz rysunek).
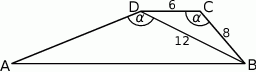
Wówczas długość ramienia 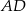 tego trapezu jest równa
tego trapezu jest równa
A) 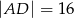 B)
B) 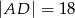 C)
C) 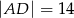 D)
D) 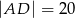
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 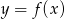 , której dziedziną jest zbiór
, której dziedziną jest zbiór 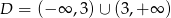 .
.
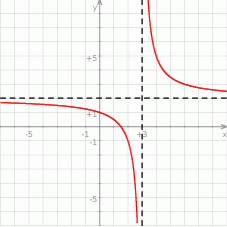
Równanie 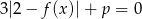 z niewiadomą
z niewiadomą  ma dokładnie dwa rozwiązania tylko wtedy, gdy
ma dokładnie dwa rozwiązania tylko wtedy, gdy
A) 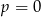 B)
B) 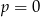 lub
lub 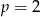 C)
C) 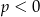 D)
D) 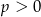
Liczba 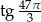 jest równa
jest równa
A) 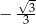 B)
B) 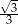 C)
C) 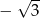 D)
D) 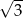
Granica 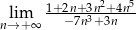 jest równa
jest równa
A) 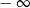 B)
B) 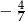 C) 0 D)
C) 0 D) 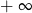
Zadania otwarte
Wśród 200 uczniów pewnego krakowskiego gimnazjum przeprowadzono ankietę dotyczącą planów wakacyjnych. Wyniki ankiety przedstawiono w tabeli.
| Klasa | Liczba uczniów | Liczba uczniów, którzy nie wyjadą na wakacje | Liczba uczniów, którzy wyjadą z rodzicami | Liczba uczniów, którzy wyjadą na kolonie |
| Pierwsza | 50 | 8 | 36 | 12 |
| Druga | 80 | 16 | 48 | 24 |
| Trzecia | 70 | 12 | 40 | 24 |
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, wyjedzie na wakacje, jeśli wiadomo, że ta osoba nie jest uczniem drugiej klasy.
Oblicz sumę 50 początkowych wyrazów ciągu 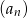 , który określony jest w następujący sposób
, który określony jest w następujący sposób
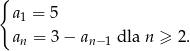
Wykaż, że dla dowolnych liczb ujemnych  spełniona jest nierówność
spełniona jest nierówność
Dany jest równoległobok 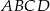 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 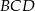 jest styczny do przekątnej
jest styczny do przekątnej 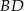 w punkcie
w punkcie 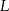 , a okrąg wpisany w trójkąt
, a okrąg wpisany w trójkąt 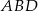 ma środek
ma środek 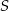 i jest styczny do boku
i jest styczny do boku 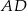 w punkcie
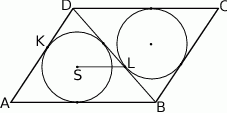
w punkcie 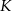 .
.
Wykaż, że jeżeli odcinek 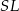 jest równoległy do prostej
jest równoległy do prostej 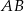 , to
, to 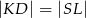 .
.
Liczba 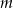 jest sumą odwrotności dwóch różnych pierwiastków równania
jest sumą odwrotności dwóch różnych pierwiastków równania
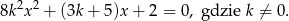
Wyznacz zbiór wartości funkcji określonej wzorem 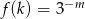 .
.
Oblicz, ile jest wszystkich liczb naturalnych pięciocyfrowych, w których zapisie występują dokładnie trzy cyfry parzyste.
Na jednym z ramion kąta ostrego o wierzchołku 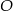 i mierze
i mierze  wybrano punkty
wybrano punkty 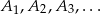 , a na drugim ramieniu punkty
, a na drugim ramieniu punkty 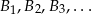 w ten sposób, że
w ten sposób, że 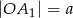 ,
, 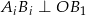 oraz
oraz 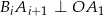 dla wszystkich
dla wszystkich 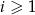 .
.
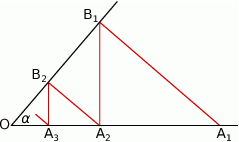
Wykaż, że długość nieskończonej łamanej 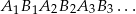 jest równa
jest równa 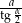 .
.
Wyznacz przedziały monotoniczności funkcji 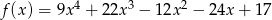 .
.
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego  jest równa
jest równa  , a wysokość tego ostrosłupa ma długość
, a wysokość tego ostrosłupa ma długość 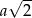 . Punkty
. Punkty  i
i 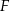 są środkami krawędzi bocznych odpowiednio
są środkami krawędzi bocznych odpowiednio 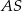 i
i 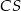 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 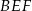 .
.
Punkt 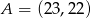 jest wierzchołkiem trójkąta prostokątnego o polu
jest wierzchołkiem trójkąta prostokątnego o polu 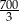 . Prosta
. Prosta 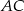 zawiera przeciwprostokątną tego trójkąta, a prosta zwierająca przyprostokątną
zawiera przeciwprostokątną tego trójkąta, a prosta zwierająca przyprostokątną 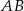 ma równanie
ma równanie 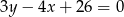 . Środek okręgu wpisanego w trójkąt
. Środek okręgu wpisanego w trójkąt 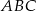 ma współrzędne
ma współrzędne 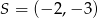 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 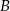 i
i 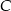 tego trójkąta.
tego trójkąta.
Częścią wspólną płaszczyzny 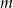 i kuli
i kuli 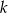 o środku
o środku 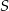 i promieniu
i promieniu 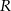 jest koło
jest koło  . Jaka musi być odległość płaszczyzny
. Jaka musi być odległość płaszczyzny 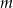 od środka kuli
od środka kuli 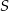 , aby stożek o podstawie
, aby stożek o podstawie  i wierzchołku
i wierzchołku 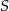 miał największą możliwą objętość? Oblicz tę maksymalną objętość.
miał największą możliwą objętość? Oblicz tę maksymalną objętość.

