/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 9 marca 2013 Czas pracy: 180 minut
Zbadaj liczbę rozwiązań układu równań w zależności od parametru 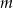
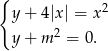
Wykaż, że jeżeli 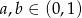 to prawdziwa jest nierówność
to prawdziwa jest nierówność
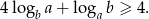
Rozwiąż nierówność 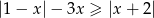 .
.
Rozwiąż równanie 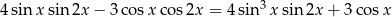 w przedziale
w przedziale 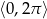 .
.
Liczby dodatnie 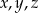 są wyrazami ciągu geometrycznego o numerach równych odpowiednio
są wyrazami ciągu geometrycznego o numerach równych odpowiednio 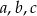 , a liczby
, a liczby 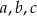 są kolejnymi wyrazami ciągu geometrycznego. Wykaż, że
są kolejnymi wyrazami ciągu geometrycznego. Wykaż, że
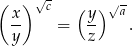
Wyznacz wszystkie wartości parametru 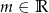 , dla których równanie
, dla których równanie 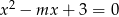 ma dwa różne pierwiastki
ma dwa różne pierwiastki 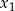 i
i 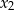 takie, że
takie, że 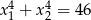 .
.
Przekątne deltoidu 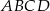 przecinają się w punkcie
przecinają się w punkcie 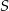 , który znajduje się w III ćwiartce układu współrzędnych. Wyznacz równanie okręgu opisanego na trójkącie
, który znajduje się w III ćwiartce układu współrzędnych. Wyznacz równanie okręgu opisanego na trójkącie 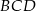 jeżeli okręgi opisane na trójkątach
jeżeli okręgi opisane na trójkątach 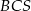 i
i 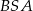 mają odpowiednio równania
mają odpowiednio równania 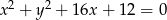 i
i 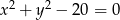 .
.
Suma długości dwóch boków trójkąta jest równa 4, a kąt zawarty między nimi ma miarę 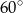 . Oblicz najmniejszą możliwą wartość obwodu trójkąta.
. Oblicz najmniejszą możliwą wartość obwodu trójkąta.
Pięć ponumerowanych kul rozmieszczamy losowo w 5 pudełkach. Jakie jest prawdopodobieństwo, że dokładnie dwa pudełka będą puste?
Podstawą ostrosłupa 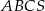 jest trójkąt
jest trójkąt 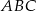 , w którym
, w którym 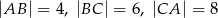 . Wszystkie ściany boczne tworzą z płaszczyzną podstawy kąt
. Wszystkie ściany boczne tworzą z płaszczyzną podstawy kąt 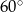 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.

