/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 30 kwietnia 2011 Czas pracy: 180 minut
Rozwiąż nierówność 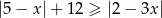 .
.
Trójkąt ostrokątny, którego boki mają długości 17 i 16 ma pole równe 64. Oblicz promień okręgu opisanego na tym trójkącie.
Wyznacz wszystkie wartości parametru 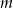 , dla których równanie
, dla których równanie 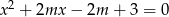 ma dwa różne pierwiastki należące do przedziału
ma dwa różne pierwiastki należące do przedziału 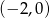 .
.
Przekątne trapezu przecinają się w punkcie 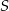 . Przez punkt
. Przez punkt 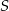 poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach
poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach 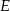 i
i 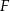 . Wykaż, że
. Wykaż, że 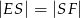 .
.
Liczby  i
i 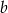 są pierwiastkami równania
są pierwiastkami równania 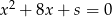 , a liczby
, a liczby  i
i 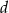 są pierwiastkami równania
są pierwiastkami równania 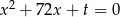 . Ciąg
. Ciąg 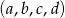 jest malejącym ciągiem geometrycznym. Oblicz
jest malejącym ciągiem geometrycznym. Oblicz  i
i 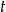 .
.
Napisz równanie okręgu opisanego na trójkącie o wierzchołkach 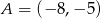 ,
, 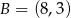 i
i 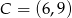 .
.
Rozwiąż nierówność 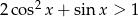 , gdzie
, gdzie 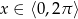 .
.
Wykaż, że jeżeli żadne dwie spośród liczb 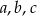 nie są równe oraz liczby
nie są równe oraz liczby 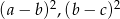 i
i 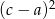 tworzą ciąg arytmetyczny, to liczby
tworzą ciąg arytmetyczny, to liczby 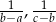 i
i 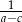 również tworzą ciąg arytmetyczny.
również tworzą ciąg arytmetyczny.
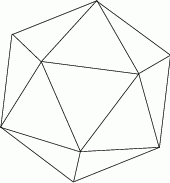
Każda ściana dwudziestościanu foremnego 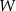 jest trójkątem równobocznym, a z każdego wierzchołka tej bryły wychodzi 5 krawędzi. Wybieramy losowo dwa różne wierzchołki wielościanu
jest trójkątem równobocznym, a z każdego wierzchołka tej bryły wychodzi 5 krawędzi. Wybieramy losowo dwa różne wierzchołki wielościanu 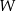 . Jakie jest prawdopodobieństwo tego, że odcinek łączący te dwa wierzchołki nie jest krawędzią wielościanu
. Jakie jest prawdopodobieństwo tego, że odcinek łączący te dwa wierzchołki nie jest krawędzią wielościanu 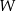 ?
?
Wyznacz wszystkie wartości parametru 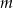 , dla którego wielomian
, dla którego wielomian 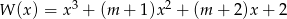 ma trzy różne pierwiastki rzeczywiste.
ma trzy różne pierwiastki rzeczywiste.
W kulę wpisano walec w ten sposób, że objętość walca stanowi 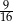 objętości kuli. Oblicz stosunek promienia kuli do wysokości walca.
objętości kuli. Oblicz stosunek promienia kuli do wysokości walca.

