/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 2 marca 2013 Czas pracy: 180 minut

Zadanie 1
(4 pkt)

Wyznacz zbiór wartości funkcji 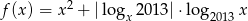2 f(x) = x + | logx 201 3|⋅log2013x .

Zadanie 2
(5 pkt)

Rozwiąż nierówność

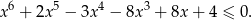
x6 + 2x5 − 3x4 − 8x3 + 8x + 4 ≤ 0.

Zadanie 3
(4 pkt)

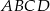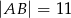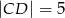Oblicz pole trapezu ABCD , którego podstawy mają długości |AB | = 11 i |CD | = 5 , a ramiona mają długości 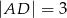|AD | = 3 i |BC | = 6 .

Zadanie 4
(4 pkt)

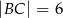Rozwiąż równanie 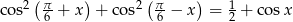( ) ( ) cos2 π6 + x + cos2 π6-− x = 12 + cosx .

Zadanie 5
(6 pkt)

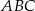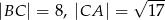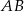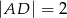W trójkącie prostokątnym ABC przyprostokątne mają długości √ --- |BC | = 8, |CA | = 1 7 . Na boku AB wybrano punkt D tak, że |AD | = 2 . Oblicz sinus kąta DCA .

Zadanie 6
(4 pkt)

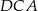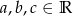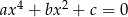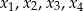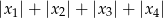Dane są liczby a,b,c ∈ R takie, że równanie 4 2 ax + bx + c = 0 ma cztery rozwiązania rzeczywiste x1,x2,x3,x4 . Oblicz wartość wyrażenia |x1|+ |x2|+ |x 3|+ |x4| .

Zadanie 7
(4 pkt)

Cztery liczby tworzą ciąg geometryczny, przy czym suma pierwszej i czwartej jest równa 27, a iloczyn drugiej i trzeciej jest równy 72. Wyznacz te liczby.

Zadanie 8
(6 pkt)

Wielomian 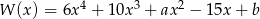W (x) = 6x4 + 10x 3 + ax 2 − 1 5x+ b jest podzielny przez trójmian 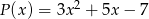P (x) = 3x 2 + 5x − 7 . Wyznacz liczby a i b .

Zadanie 9
(4 pkt)

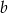Oblicz prawdopodobieństwo, że w dziesięciu rzutach kostką dokładnie na dwóch kostkach otrzymamy ściankę z dwoma oczkami i dokładnie na trzech kostkach ściankę z trzema oczkami.

Zadanie 10
(5 pkt)

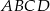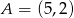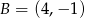Pole równoległoboku ABCD o danych wierzchołkach A = (5,2) i B = (4,− 1) jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej 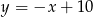y = −x + 10 , który ma obie współrzędne będące liczbami całkowitymi.

Zadanie 11
(4 pkt)

Oblicz odległość środka ściany sześcianu o krawędzi długości a od przekątnej tego sześcianu.

Arkusz Wersja PDF
Rozwiązania