/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom rozszerzony 23 maja 2017 Czas pracy: 180 minut
Zadania zamknięte
Suma wszystkich współczynników wielomianu 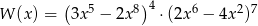 jest równa
jest równa
A) 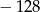 B) 216 C) 64 D)
B) 216 C) 64 D) 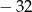
Funkcja 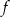 określona jest wzorem
określona jest wzorem
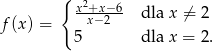
Zbiorem wartości funkcji 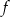 jest
jest
A) 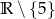 B)
B) 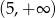 C)
C) 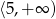 D)
D) 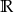
Najmniejszą liczbą w zbiorze rozwiązań nierówności 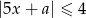 jest liczba 150. Liczba
jest liczba 150. Liczba  jest równa
jest równa
A) 600 B) 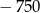 C)
C) 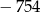 D) 754
D) 754
Czworokąty 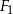 i
i 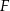 są podobne. Pole czworokąta
są podobne. Pole czworokąta 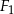 jest o 36% mniejsze od pola czworokąta
jest o 36% mniejsze od pola czworokąta 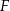 . Obwód czworokąta
. Obwód czworokąta 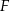 jest większy od obwodu czworokąta
jest większy od obwodu czworokąta 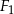 o:
o:
A) 20% B) 25% C) 36% D) 18%
Liczba 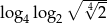 jest równa
jest równa
A) 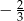 B)
B) 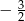 C) 0,5 D)
C) 0,5 D) 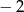
Zadania otwarte
Między liczbami rzeczywistymi  i
i 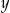 zachodzi związek
zachodzi związek 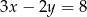 . Wyznacz najmniejszą wartość wyrażenia
. Wyznacz najmniejszą wartość wyrażenia 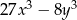 .
.
Oblicz granicę 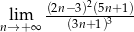 .
.
Niech 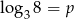 . Wykaż, że
. Wykaż, że 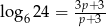 .
.
Wykaż, że proste przechodzące przez wierzchołek równoległoboku i środki boków, do których on nie należy, dzielą przekątną równoległoboku na trzy równe części.
Dany jest ciąg określony wzorem 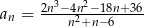 .
.
- Wykaż, że wszystkie wyrazy tego ciągu są liczbami całkowitymi.
- Sprawdź, czy jest to ciąg arytmetyczny.
Suma dwóch liczb, ich iloczyn i różnica ich kwadratów są równe. Wyznacz te liczby.
Okrąg o promieniu 4 jest wpisany w trójkąt. Punkt styczności podzielił jeden z boków na odcinki o długości 6 i 8. Oblicz długości boków tego trójkąta.
Wiadomo, że 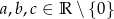 oraz
oraz 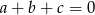 . Oblicz wartość sumy
. Oblicz wartość sumy
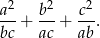
Iloczyn trzech kolejnych liczb nieparzystych jest o 65 większy od różnicy kwadratów liczby największej i najmniejszej. Znajdź te liczby.
Dany jest okrąg o promieniu 11 oraz punkt 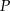 oddalony o 7 od środka okręgu. Przez punkt
oddalony o 7 od środka okręgu. Przez punkt 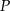 poprowadzono cięciwę o długości 18. W jakim stosunku punkt
poprowadzono cięciwę o długości 18. W jakim stosunku punkt 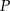 podzielił tę cięciwę na dwa odcinki?
podzielił tę cięciwę na dwa odcinki?
Rozwiąż nierówność