/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki (stara formuła)
poziom rozszerzony 9 maja 2019 Czas pracy: 180 minut
Funkcja 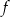 jest określona wzorem
jest określona wzorem 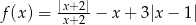 , dla każdej liczby rzeczywistej
, dla każdej liczby rzeczywistej 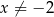 . Wyznacz zbiór wartości tej funkcji.
. Wyznacz zbiór wartości tej funkcji.
Udowodnij, że dla dowolnych dodatnich liczb rzeczywistych  i
i 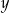 , takich że
, takich że 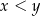 , i dowolnej dodatniej liczby rzeczywistej
, i dowolnej dodatniej liczby rzeczywistej  , prawdziwa jest nierówność
, prawdziwa jest nierówność 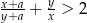 .
.
Dany jest trójkąt równoramienny 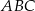 , w którym
, w którym 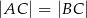 . Na ramieniu
. Na ramieniu 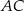 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 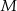 (
(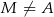 i
i 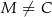 ), a na ramieniu
), a na ramieniu 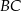 wybrano punkt
wybrano punkt 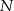 , w taki sposób, że
, w taki sposób, że 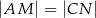 . Przez punkty
. Przez punkty 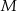 i
i 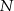 poprowadzono proste prostopadłe do podstawy
poprowadzono proste prostopadłe do podstawy 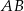 tego trójkąta, które wyznaczają na niej punkty
tego trójkąta, które wyznaczają na niej punkty 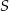 i
i 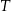 . Udowodnij, że
. Udowodnij, że 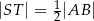 .
.
Ciąg 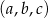 jest geometryczny, ciąg
jest geometryczny, ciąg 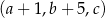 jest malejącym ciągiem arytmetycznym oraz
jest malejącym ciągiem arytmetycznym oraz 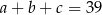 . Oblicz
. Oblicz 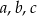 .
.
Dane są okręgi o równaniach 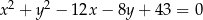 i
i 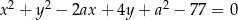 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru  , dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
, dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
Wielomian określony wzorem 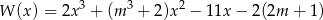 jest podzielny przez dwumian
jest podzielny przez dwumian 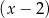 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 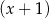 daje resztę 6. Oblicz
daje resztę 6. Oblicz 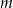 oraz pierwiastki wielomianu
oraz pierwiastki wielomianu 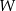 dla wyznaczonej wartości
dla wyznaczonej wartości 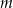 .
.
Rozwiąż równanie 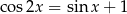 w przedziale
w przedziale 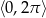 .
.
Punkt 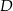 leży na boku
leży na boku 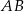 trójkąta
trójkąta 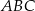 oraz
oraz 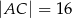 ,
, 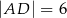 ,
, 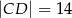 i
i 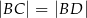 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 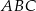 .
.
Wyznacz wszystkie wartości parametru 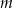 , dla których funkcja kwadratowa
, dla których funkcja kwadratowa 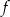 określona wzorem
określona wzorem
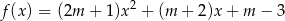
ma dwa różne pierwiastki rzeczywiste 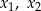 spełniające warunek
spełniające warunek 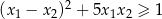 .
.
Ze zbioru 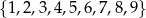 losujemy kolejno ze zwracaniem trzy liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie spośród trzech wylosowanych liczb będą równe. Wynik zapisz w postaci ułamka nieskracalnego.
losujemy kolejno ze zwracaniem trzy liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie spośród trzech wylosowanych liczb będą równe. Wynik zapisz w postaci ułamka nieskracalnego.
Podstawą ostrosłupa 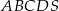 jest prostokąt
jest prostokąt 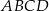 , którego boki mają długości
, którego boki mają długości 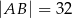 i
i 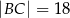 . Ściany boczne
. Ściany boczne 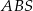 i
i 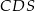 są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem
są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem  . Ściany boczne
. Ściany boczne 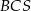 i
i 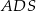 są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem
są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem 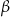 . Miary kątów
. Miary kątów  i
i 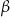 spełniają warunek:
spełniają warunek: 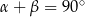 . Oblicz
. Oblicz 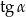 oraz pole powierzchni całkowitej tego ostrosłupa.
oraz pole powierzchni całkowitej tego ostrosłupa.

