/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 11 kwietnia 2015 Czas pracy: 170 minut
Zadania zamknięte
Jeśli 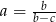 , to
, to
A) 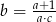 B)
B) 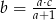 C)
C) 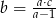 D)
D) 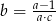
Liczba 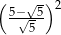 jest równa
jest równa
A) 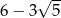 B) 4 C)
B) 4 C) 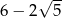 D) 6
D) 6
Liczba 1,1 jest przybliżeniem z niedomiarem liczby 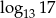 i błąd bezwzględny tego przybliżenia jest mniejszy od 0,01. Liczba
i błąd bezwzględny tego przybliżenia jest mniejszy od 0,01. Liczba
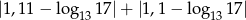
jest równa
A) 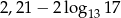 B) 0,01 C)
B) 0,01 C) 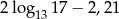 D) 2,21
D) 2,21
Okrąg o średnicy 6 jest styczny do osi 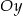 , a oś
, a oś 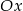 jest jego osią symetrii. Środek tego okręgu ma współrzędne
jest jego osią symetrii. Środek tego okręgu ma współrzędne
A) 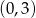 B)
B) 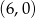 C)
C) 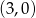 D)
D) 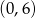
Dane są dwie funkcje określone dla wszystkich liczb rzeczywistych  wzorami
wzorami 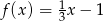 oraz
oraz 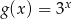 . Liczba punktów wspólnych wykresów tych funkcji jest równa
. Liczba punktów wspólnych wykresów tych funkcji jest równa
A) 3 B) 2 C) 1 D) 0
Punkty 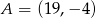 i
i 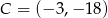 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 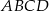 . Przekątne tego kwadratu przecinają się w punkcie
. Przekątne tego kwadratu przecinają się w punkcie
A) 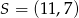 B)
B) 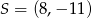 C)
C) 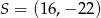 D)
D) 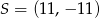
Wskaż równość fałszywą.
A) 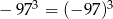 B)
B) 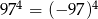 C)
C) 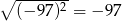 D)
D) 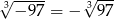
Kąt  jest ostry i spełniona jest równość
jest ostry i spełniona jest równość 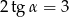 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 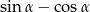 jest równa
jest równa
A) 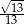 B)
B) 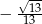 C) 0 D)
C) 0 D) 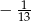
Liczba osób planujących wziąć udział w demonstracji początkowo wzrosła o 30%, a po dwóch dniach zmalała o 40%. W wyniku tych dwóch zmian liczba osób planujących wziąć udział w demonstracji zmalała o
A) 24% B) 10% C) 78% D) 22%
Na płaszczyźnie dane są punkty: 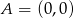 ,
, 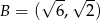 i
i 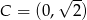 . Kąt
. Kąt 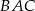 jest równy
jest równy
A) 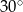 B)
B) 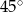 C)
C) 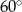 D)
D) 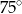
Funkcja 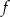 , określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie
, określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie  resztę z dzielenia tej liczby przez 7. Która z poniższych funkcji nie ma miejsca zerowego?
resztę z dzielenia tej liczby przez 7. Która z poniższych funkcji nie ma miejsca zerowego?
A) 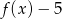 B)
B) 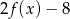 C)
C) 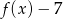 D)
D) 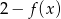
Na rysunku przedstawiony jest ostrosłup prawidłowy trójkątny 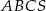 . Kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa oznaczono literą:
. Kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa oznaczono literą:
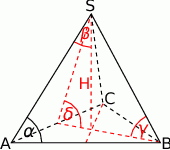
A)  B)
B) 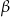 C)
C) 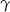 D)
D) 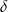
Ekipa złożona z 16 pracowników wykonała dach hali przemysłowej w ciągu 65 dni. Jeżeli dach na drugiej takiej samej hali trzeba wykonać w ciągu 52 dni, to, przy założeniu takiej samej wydajności, należy zatrudnić do pracy o
A) 2 osoby więcej. B) 4 osoby więcej. C) 6 osób więcej. D) 8 osób więcej.
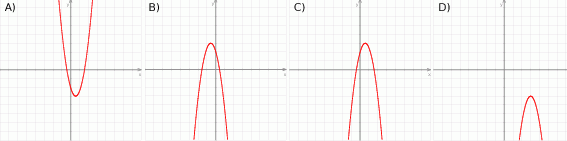
Który z rysunków może przedstawiać wykres funkcji kwadratowej 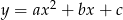 takiej, że
takiej, że 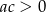 ?
?
Równanie 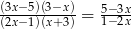 ma dwa rozwiązania. Są to liczby:
ma dwa rozwiązania. Są to liczby:
A) 3 i 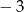 B) 3 i
B) 3 i 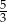 C) 0 i 3 D) 0 i
C) 0 i 3 D) 0 i 
Liczba 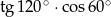 jest równa liczbie
jest równa liczbie
A) 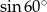 B)
B) 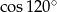 C)
C) 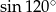 D)
D) 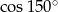
Krótsza przekątna rombu o boku długości 6 tworzy z jego bokiem kąt o mierze 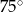 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 18 B) 9 C) 36 D) 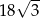
Tworząca stożka ma długość 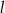 , a promień jego podstawy jest równy
, a promień jego podstawy jest równy  (zobacz rysunek).
(zobacz rysunek).
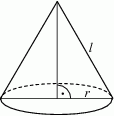
Powierzchnia boczna tego stożka jest 3 razy większa od pola jego podstawy. Wówczas
A) 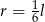 B)
B) 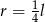 C)
C) 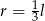 D)
D) 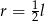
Suma dwunastu początkowych wyrazów ciągu arytmetycznego 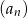 jest równa 42. Pierwszy wyraz
jest równa 42. Pierwszy wyraz 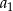 tego ciągu jest równy 4. Wtedy
tego ciągu jest równy 4. Wtedy
A) 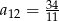 B)
B) 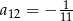 C)
C) 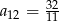 D)
D) 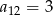
Jeżeli trójkąty 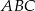 i
i 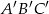 są podobne, a ich obwody są odpowiednio równe 25 cm i 50 cm, to skala podobieństwa trójkątów
są podobne, a ich obwody są odpowiednio równe 25 cm i 50 cm, to skala podobieństwa trójkątów 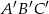 i
i 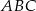 jest równa
jest równa
A) 2 B) 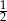 C)
C) 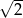 D)
D) 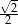
Dany jest ciąg geometryczny 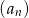 , w którym
, w którym 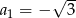 ,
, 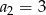 ,
, 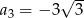 . Dziewiąty wyraz tego ciągu, czyli
. Dziewiąty wyraz tego ciągu, czyli 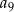 , jest równy
, jest równy
A) 243 B) 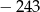 C)
C) 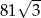 D)
D) 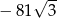
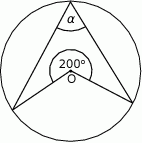
Punkt 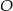 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  przedstawiony na rysunku ma miarę:
przedstawiony na rysunku ma miarę:
A) 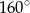 B)
B) 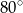 C)
C) 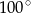 D)
D) 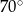
Rzucamy jeden raz symetryczną sześcienną kostką do gry. Niech 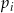 oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez
oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez 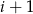 . Wtedy
. Wtedy
A) 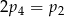 B)
B) 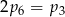 C)
C) 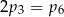 D)
D) 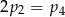
Na okręgu wybrano 20 punktów i połowę z nich pomalowano na biało, a drugą połowę na czarno. Ile jest odcinków o końcach w tych punktach, których jeden koniec jest biały, a drugi czarny?
A) 380 B) 190 C) 90 D) 100
Zadania otwarte
Wyznacz wszystkie liczby naturalne  , dla których
, dla których 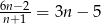 .
.
Wykaż, że dla dowolnej liczby całkowitej 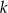 prawdziwa jest nierówność
prawdziwa jest nierówność 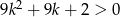 .
.
Udowodnij, że po wymnożeniu kolejnych liczb naturalnych od 1 do 30, czyli po wykonaniu działania 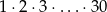 , otrzymamy liczbę, która kończy się dokładnie 7 zerami.
, otrzymamy liczbę, która kończy się dokładnie 7 zerami.
Koło 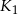 ma promień długości
ma promień długości  . Wewnątrz tego koła rysujemy kolejno koła
. Wewnątrz tego koła rysujemy kolejno koła 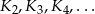 takie, że kolejne koło ma średnicę równą promieniowi poprzedniego koła.
takie, że kolejne koło ma średnicę równą promieniowi poprzedniego koła.
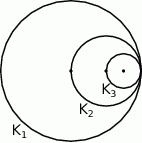
Wyznacz pole koła 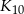 .
.
W trójkącie prostokątnym 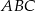 , w którym
, w którym 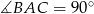 i
i 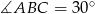 , wybrano na przyprostokątnej
, wybrano na przyprostokątnej 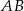 punkt
punkt 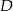 tak, że
tak, że 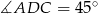 . Oblicz stosunek długości odcinków
. Oblicz stosunek długości odcinków 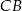 i
i 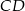 .
.
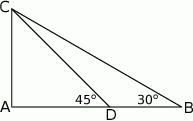
Przeciwprostokątna trójkąta prostokątnego o obwodzie 40 ma długość 17. Oblicz długości przyprostokątnych tego trójkąta.
W prostokącie 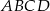 dane są
dane są 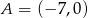 ,
, 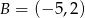 i
i 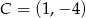 . Napisz równanie prostej, która jest styczna w punkcie
. Napisz równanie prostej, która jest styczna w punkcie 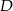 do okręgu opisanego na prostokącie
do okręgu opisanego na prostokącie 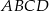 .
.
Samochód przejechał połowę trasy ze średnią prędkością 40 km/h. Na całej trasie średnia prędkość samochodu była równa 48 km/h. Oblicz z jaką średnią prędkością samochód przejechał pozostałą część trasy.
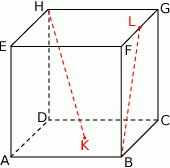
Punkty 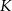 i
i 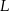 są środkami odpowiednio podstawy
są środkami odpowiednio podstawy 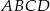 i krawędzi
i krawędzi 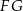 sześcianu
sześcianu 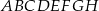 . Suma kwadratów długości odcinków
. Suma kwadratów długości odcinków 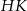 i
i 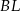 jest równa 33. Oblicz pole powierzchni całkowitej sześcianu.
jest równa 33. Oblicz pole powierzchni całkowitej sześcianu.