/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 10 maja 2008 Czas pracy: 180 minut
Dana jest funkcja 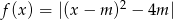 , gdzie
, gdzie 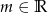 .
.
- Naszkicuj wykres funkcji
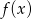 dla
dla 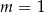 .
. - Dla jakich wartości parametru
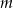 równanie
równanie 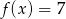 ma dokładnie trzy rozwiązania.
ma dokładnie trzy rozwiązania.
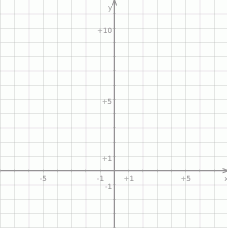
Latarnię uliczną umieszczono w odległości 5 m od naroża budynku – tak jak jest to pokazane na rysunku. Wiedząc, że światło latarni oświetla obszar w promieniu 10 m od źródła światła, oblicz jakie jest pole obszaru oświetlanego latarnią.
W trójkącie 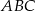 dane są
dane są 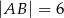 ,
, 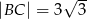 oraz
oraz 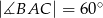 . Oblicz pole trójkąta
. Oblicz pole trójkąta 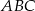 .
.
Wiedząc, że suma kwadratów pierwiastków równania
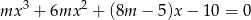
jest równa 30, wyznacz 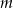 .
.
Niech 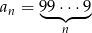 . Oblicz sumę 12 początkowych wyrazów ciągu
. Oblicz sumę 12 początkowych wyrazów ciągu 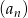 .
.
Wierzchołkami kwadratu 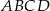 są punkty o współrzędnych
są punkty o współrzędnych 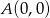 ,
, 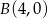 ,
, 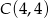 i
i 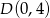 . Dla każdej liczby rzczywistej
. Dla każdej liczby rzczywistej 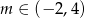 rozważamy trójkąt o wierzchołkach
rozważamy trójkąt o wierzchołkach 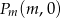 ,
, 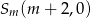 i
i 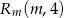 . Wyznacz wszystkie wartości prametru
. Wyznacz wszystkie wartości prametru 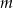 , dla których pole figury, która jest częścią wspólną kwadratu
, dla których pole figury, która jest częścią wspólną kwadratu 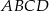 i trójkąta
i trójkąta 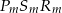 wynosi 2.
wynosi 2.
Sześcian, którego ściany zostały pomalowane czerwoną farbą, dzielimy 6 płaszczyznami równoległymi do jego ścian na 27 identycznych sześcianików. Losujemy 2 spośród nich.
- Oblicz prawdopodobieństwo, że łączna liczba czerwonych ścian wylosowanych sześcianików wynosi 3.
- Oblicz prawdopodobieństwo, że wylosowane sześcianiki mają wspólną ścianę.
- Wyznacz wszystkie liczby
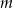 , dla których istnieją dwie liczby rzeczywiste, których suma i iloczyn są równe
, dla których istnieją dwie liczby rzeczywiste, których suma i iloczyn są równe 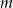 .
. - Uzasadnij, że jeżeli suma i iloczyn dwóch liczb rzeczywistych jest równa liczbie dodatniej
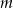 , to suma sześcianów tych liczb jest nie mniejsza niż 16.
, to suma sześcianów tych liczb jest nie mniejsza niż 16.
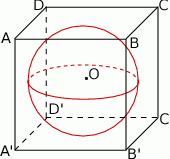
Płaszczyzna 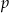 jest styczna do kuli wpisanej w sześcian
jest styczna do kuli wpisanej w sześcian 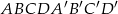 o krawędzi długości
o krawędzi długości 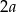 oraz przecina krawędzie
oraz przecina krawędzie 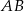 ,
, 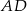 i
i 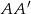 w takich punktach
w takich punktach 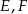 i
i 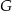 odpowiednio, że
odpowiednio, że 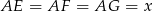 . Wykonaj odpowiedni rysunek i wyznacz
. Wykonaj odpowiedni rysunek i wyznacz  .
.
Funkcje 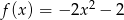 ,
, 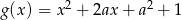 i
i 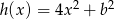 mają tę własność, że dla każdej liczby rzeczywistej
mają tę własność, że dla każdej liczby rzeczywistej  , liczby
, liczby 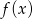 ,
, 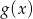 i
i 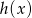 tworzą (w pewnej kolejności) ciąg geometryczny. Wyznacz możliwe ilorazy tego ciągu.
tworzą (w pewnej kolejności) ciąg geometryczny. Wyznacz możliwe ilorazy tego ciągu.
W trójkącie prostokątnym jedna z przyprostokątnych jest średnią arytmetyczną drugiej przyprostokątnej i przeciwprostokątnej. Oblicz sinusy kątów ostrych tego trójkąta.

