/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony 4 czerwca 2013 Czas pracy: 180 minut
Rozwiąż nierówność 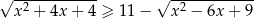 .
.
Wyznacz wszystkie wartości parametru 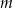 , dla których równanie
, dla których równanie 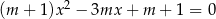 ma dwa różne pierwiastki takie, że ich suma jest nie większa niż 2,5.
ma dwa różne pierwiastki takie, że ich suma jest nie większa niż 2,5.
Rozwiąż równanie 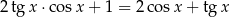 w przedziale
w przedziale 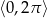 .
.
Wykaż, że prawdziwa jest równość 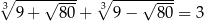 .
.
Uzasadnij, że jeżeli 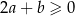 , to
, to 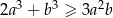 .
.
W równoległoboku 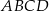 miara kąta ostrego jest równa
miara kąta ostrego jest równa 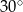 , a odległości punktu przecięcia się przekątnych od sąsiednich boków równoległoboku są równe 2 i
, a odległości punktu przecięcia się przekątnych od sąsiednich boków równoległoboku są równe 2 i 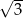 . Oblicz długość krótszej przekątnej tego równoległoboku.
. Oblicz długość krótszej przekątnej tego równoległoboku.
Punkty 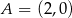 i
i 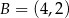 leżą na okręgu o równaniu
leżą na okręgu o równaniu 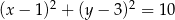 . Wyznacz na tym okręgu taki punkt
. Wyznacz na tym okręgu taki punkt 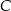 , aby trójkąt
, aby trójkąt 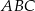 był trójkątem równoramiennym o podstawie
był trójkątem równoramiennym o podstawie 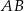 .
.
Wykaż, że dla dowolnego kąta  prawdziwa jest tożsamość
prawdziwa jest tożsamość 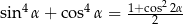 .
.
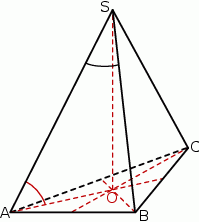
Podstawą ostrosłupa prawidłowego trójkątnego 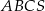 jest trójkąt
jest trójkąt 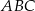 . Kąt nachylenia krawędzi bocznej
. Kąt nachylenia krawędzi bocznej 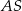 do płaszczyzny podstawy ostrosłupa jest równy kątowi między krawędziami bocznymi
do płaszczyzny podstawy ostrosłupa jest równy kątowi między krawędziami bocznymi 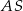 i
i 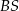 zawartymi w ścianie bocznej
zawartymi w ścianie bocznej 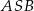 tego ostrosłupa (zob. rysunek). Oblicz kosinus tego kąta.
tego ostrosłupa (zob. rysunek). Oblicz kosinus tego kąta.
Liczby 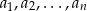 są dodatnie i w podanej kolejności tworzą ciąg geometryczny. Uzasadnij, że prawdziwa jest równość
są dodatnie i w podanej kolejności tworzą ciąg geometryczny. Uzasadnij, że prawdziwa jest równość 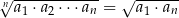 .
.
Suma długości dwóch boków trójkąta równa się 4, a kąt między tymi bokami ma miarę 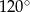 . Oblicz najmniejszą wartość sumy kwadratów długości wszystkich boków tego trójkąta.
. Oblicz najmniejszą wartość sumy kwadratów długości wszystkich boków tego trójkąta.
Pierwiastkami wielomianu stopnia trzeciego są liczby 1, 3, 5. Współczynnik przy najwyższej potędze zmiennej tego wielomianu jest równy 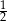 . Uzasadnij, że dla każdej liczby całkowitej nieparzystej wartość tego wielomianu jest liczbą podzielną przez 24.
. Uzasadnij, że dla każdej liczby całkowitej nieparzystej wartość tego wielomianu jest liczbą podzielną przez 24.

