/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom rozszerzony 23 maja 2018 Czas pracy: 180 minut
Zadania zamknięte
Liczba 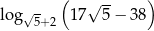 jest równa
jest równa
A) 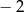 B)
B) 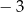 C)
C) 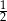 D)
D) 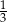
Trójkąt 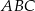 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 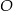 . Jeśli
. Jeśli 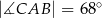 i
i 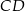 jest średnicą okręgu, to miara kąta
jest średnicą okręgu, to miara kąta 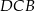 jest równa
jest równa
A) 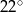 B)
B) 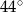 C)
C) 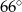 D)
D) 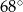
Wskaż nierówność, która opisuje zbiór zaznaczony na osi liczbowej.
![]()
A) 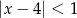 B)
B) 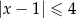 C)
C) 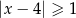 D)
D) 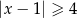
Jeśli 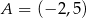 i
i 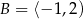 , to różnica przedziałów
, to różnica przedziałów 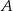 i
i 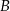 jest równa
jest równa
A) 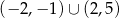 B)
B) 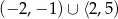 C)
C) 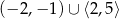 D)
D) 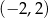
Jeżeli 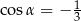 i
i  jest kątem rozwartym, to wartość
jest kątem rozwartym, to wartość 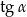 jest równa
jest równa
A) 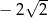 B)
B) 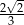 C)
C) 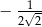 D)
D) 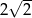
Zadania otwarte
Oblicz wartość wyrażenia 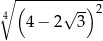 .
.
Niech 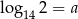 . Wyraź za pomocą
. Wyraź za pomocą  wartość logarytmu
wartość logarytmu 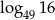 .
.
Oblicz wartość wyrażenia
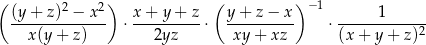
dla 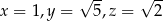 .
.
Dane są okręgi o środkach 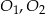 oraz promieniu 2. Jeden z nich jest styczny wewnętrznie, a drugi styczny zewnętrznie do okręgu o środku
oraz promieniu 2. Jeden z nich jest styczny wewnętrznie, a drugi styczny zewnętrznie do okręgu o środku 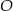 i promieniu 5. Wiadomo, że
i promieniu 5. Wiadomo, że 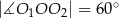 . Oblicz długość odcinka
. Oblicz długość odcinka 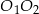 .
.
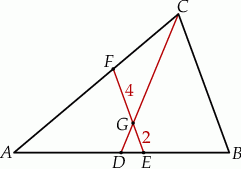
W trójkącie 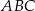 odcinek
odcinek 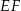 o końcach należących do boków odpowiednio
o końcach należących do boków odpowiednio 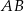 i
i 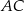 przecina środkową
przecina środkową 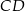 w punkcie
w punkcie 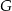 , oraz odcinek
, oraz odcinek 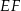 jest równoległy do odcinka
jest równoległy do odcinka 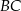 (patrz rysunek). Oblicz długość odcinka
(patrz rysunek). Oblicz długość odcinka 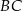 wiedząc, że
wiedząc, że 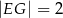 i
i 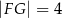 .
.
W trójkąt równoramienny wpisano kwadrat w ten sposób, że dwa jego wierzchołki leżą na podstawie trójkąta, a dwa pozostałe są środkami ramion. Jaką część pola trójkąta stanowi pole kwadratu? Odpowiedź uzasadnij.
W trójkącie równobocznym 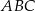 obrano na boku
obrano na boku 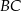 taki punkt
taki punkt 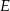 , że
, że 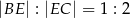 . Oblicz tangens kąta
. Oblicz tangens kąta 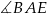 .
.
Dane są trzy okręgi o środkach 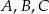 i promieniach równych odpowiednio
i promieniach równych odpowiednio 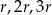 . Każde dwa z tych okręgów są zewnętrznie styczne: pierwszy z drugim w punkcie
. Każde dwa z tych okręgów są zewnętrznie styczne: pierwszy z drugim w punkcie 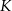 , drugi z trzecim w punkcie
, drugi z trzecim w punkcie 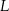 i trzeci z pierwszym w punkcie
i trzeci z pierwszym w punkcie 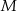 . Oblicz stosunek pola trójkąta
. Oblicz stosunek pola trójkąta 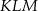 do pola trójkąta
do pola trójkąta 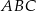 .
.
Rozwiąż równanie 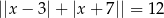 .
.
Wysokości w pewnym trójkącie 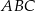 mają długości:
mają długości: 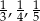 . Wykaż, że jest to trójkąt prostokątny.
. Wykaż, że jest to trójkąt prostokątny.
Uzasadnij, że dla dowolnych liczb dodatnich  i
i 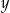 prawdziwa jest nierówność
prawdziwa jest nierówność