/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 1 kwietnia 2017 Czas pracy: 170 minut
Zadania zamknięte
Suma sześciu kolejnych potęg naturalnych liczby 2 jest równa 2016. Najmniejszą z tych liczb jest
A) 5 B) 8 C) 16 D) 32
Cenę pewnego towaru obniżono o 20%, a następnie nową cenę tego towaru obniżono o 30%. Takie dwie obniżki ceny tego towaru można zastąpić równoważną im jedną obniżką
A) o 50% B) o 56% C) o 44% D) o 66%
Liczba 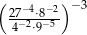 jest równa
jest równa
A) 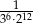 B)
B) 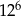 C)
C) 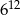 D)
D) 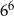
Równość 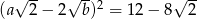 jest prawdziwa dla
jest prawdziwa dla
A) 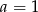 i
i 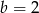 B)
B) 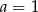 i
i 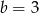 C)
C) 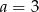 i
i 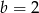 D)
D) 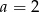 i
i 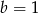
Zbiorem wartości funkcji kwadratowej 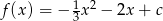 jest przedział
jest przedział 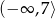 . Zatem współczynnik
. Zatem współczynnik  jest równy
jest równy
A) 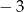 B) 4 C) 7 D) 10
B) 4 C) 7 D) 10
Różnica 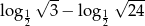 jest równa
jest równa
A) 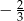 B)
B) 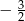 C)
C)  D)
D) 
Dana jest funkcja liniowa 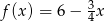 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 8 B) 6 C) 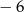 D)
D) 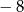
Końce odcinka 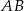 o długości 9 są środkami okręgów o promieniach 6 i 4 (zobacz rysunek).
o długości 9 są środkami okręgów o promieniach 6 i 4 (zobacz rysunek).
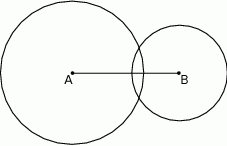
Punkt 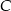 leży na odcinku
leży na odcinku 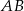 i jest środkiem takiego okręgu, o promieniu większym od 6, że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku
i jest środkiem takiego okręgu, o promieniu większym od 6, że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku 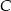 ma długość
ma długość
A) 6,5 B) 7,5 C) 8,5 D) 9,5
Przedstawiona na rysunku bryła składa się z walca i półkuli. Wysokość walca jest taka, jak promień jego podstawy i jest równa 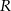 .
.
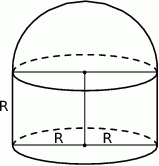
Objętość tej bryły jest równa
A) 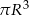 B)
B) 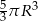 C)
C) 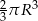 D)
D) 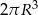
Dana jest funkcja 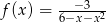 . Wskaż maksymalny zbiór, na którym funkcja
. Wskaż maksymalny zbiór, na którym funkcja 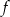 przyjmuje wartości ujemne.
przyjmuje wartości ujemne.
A) 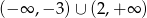 B)
B) 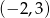 C)
C) 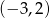 D)
D) 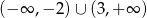
Dany jest ciąg geometryczny 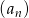 , w którym
, w którym 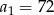 i
i 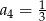 . Iloraz
. Iloraz 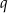 tego ciągu jest równy
tego ciągu jest równy
A) 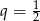 B)
B) 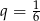 C)
C) 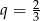 D)
D) 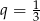
Na rysunku przedstawiono fragment prostej o równaniu 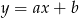 .
.
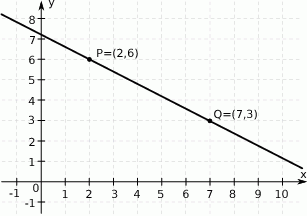
Współczynnik kierunkowy tej prostej jest równy
A) 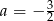 B)
B) 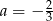 C)
C) 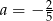 D)
D) 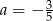
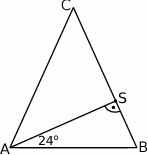
W trójkącie równoramiennym 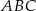 poprowadzono wysokość
poprowadzono wysokość 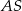 , która utworzyła z podstawą kąt o mierze
, która utworzyła z podstawą kąt o mierze 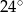 (zobacz rysunek). Ramię tego trójkąta ma długość 10. Długość wysokości
(zobacz rysunek). Ramię tego trójkąta ma długość 10. Długość wysokości 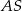 jest liczbą z przedziału
jest liczbą z przedziału
A) 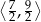 B)
B) 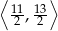 C)
C) 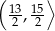 D)
D) 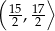
Piętnasty wyraz ciągu arytmetycznego jest równy 6, a różnica tego ciągu jest równa 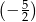 . Szósty wyraz tego ciągu jest równy
. Szósty wyraz tego ciągu jest równy
A) 16 B) 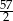 C) 21 D)
C) 21 D) 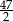
Dany jest trapez 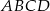 , w którym przekątna
, w którym przekątna 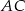 jest prostopadła do ramienia
jest prostopadła do ramienia 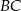 ,
, 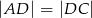 oraz
oraz 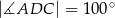 (zobacz rysunek).
(zobacz rysunek).
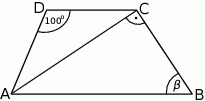
Stąd wynika, że
A) 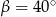 B)
B) 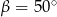 C)
C) 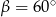 D)
D) 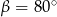
Ile jest liczb naturalnych trzycyfrowych, których iloczyn cyfr jest równy 0?
A) 162 B) 90 C) 171 D) 172
Kąt  jest ostry i
jest ostry i 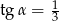 . Wtedy
. Wtedy
A) 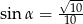 B)
B) 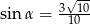 C)
C) 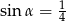 D)
D) 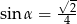
Układ równań 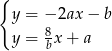 ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 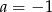 i
i 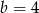 B)
B) 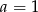 i
i 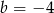 C)
C) 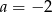 i
i 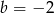 D)
D) 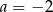 i
i 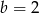
Jeżeli do zestawu czterech danych: 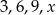 dołączymy liczbę 3, to średnia arytmetyczna wzrośnie o 2. Zatem
dołączymy liczbę 3, to średnia arytmetyczna wzrośnie o 2. Zatem
A) 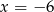 B)
B) 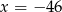 C)
C) 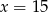 D)
D) 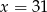
W układzie współrzędnych dane są punkty 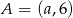 oraz
oraz 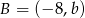 . Punkt
. Punkt 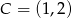 jest takim punktem odcinka
jest takim punktem odcinka 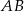 , że
, że 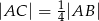 . Wynika stąd, że
. Wynika stąd, że
A) 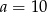 i
i 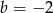 B)
B) 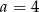 i
i 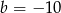 C)
C) 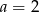 i
i 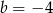 D)
D) 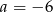 i
i 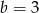
Dany jest okrąg o środku 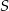 i promieniu
i promieniu  , długość łuku
, długość łuku 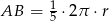 (patrz rysunek).
(patrz rysunek).
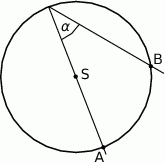
Miara kąta  jest równa
jest równa
A) 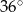 B)
B) 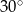 C)
C) 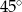 D)
D) 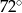
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 3, a przekątna ściany bocznej ma długość 4 (zobacz rysunek). Kąt, jaki tworzą przekątne ścian bocznych tego graniastosłupa wychodzące z jednego wierzchołka, ma miarę  .
.
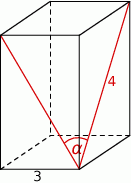
Wtedy wartość 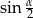 jest równa
jest równa
A)  B)
B) 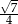 C)
C) 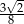 D)
D) 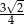
Proste prostopadłe 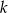 i
i 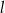 o równaniach
o równaniach 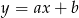 oraz
oraz 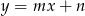 przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
A) obie liczby 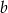 i
i  mogą być ujemne
mogą być ujemne
B) obie liczby 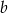 i
i  mogą być dodatnie
mogą być dodatnie
C) obie liczby 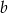 i
i  muszą być ujemne
muszą być ujemne
D) obie liczby 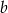 i
i  muszą być dodatnie
muszą być dodatnie
Punkty 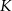 i
i 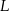 są środkami przyprostokątnych
są środkami przyprostokątnych 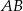 i
i 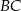 trójkąta prostokątnego
trójkąta prostokątnego 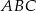 . Punkty
. Punkty 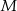 i
i 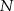 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 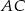 tak, że odcinki
tak, że odcinki 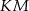 i
i 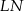 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 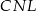 jest równe 2, a pole trójkąta
jest równe 2, a pole trójkąta 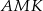 jest równe 5.
jest równe 5.
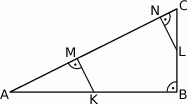
Zatem pole trójkąta 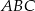 jest równe
jest równe
A) 32 B) 16 C) 28 D) 18
Średnia arytmetyczna sześciu liczb naturalnych: 21, 14, 19, 15, 24,  , jest równa
, jest równa  . Mediana tych liczb jest równa
. Mediana tych liczb jest równa
A) 17 B) 20 C) 19 D) 21
Zadania otwarte
Dane są proste o równaniach 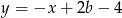 oraz
oraz 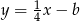 , które przecinają się w punkcie leżącym na osi
, które przecinają się w punkcie leżącym na osi 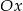 układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi
układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi 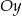 .
.
Punkt 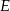 jest punktem wspólnym dwusiecznych kątów
jest punktem wspólnym dwusiecznych kątów 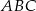 i
i 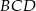 trapezu
trapezu 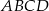 o podstawach
o podstawach 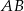 i
i 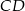 . Punkt
. Punkt 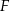 jest środkiem odcinka
jest środkiem odcinka 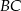 (zobacz rysunek).
(zobacz rysunek).
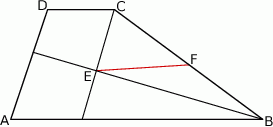
Wykaż, że 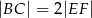 .
.
Rozwiąż nierówność 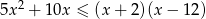 .
.
Wykaż, że jeżeli liczby rzeczywiste 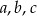 spełniają warunek
spełniają warunek 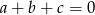 , to
, to
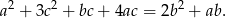
Ze zbioru liczb 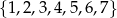 losujemy trzy razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia
losujemy trzy razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia 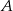 , polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 4.
, polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 4.
Dany jest ciąg arytmetyczny 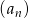 określony dla każdej liczby naturalnej
określony dla każdej liczby naturalnej 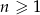 , w którym
, w którym 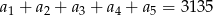 oraz
oraz 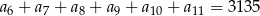 . Oblicz pierwszy wyraz, różnicę oraz najmniejszy dodatni wyraz ciągu
. Oblicz pierwszy wyraz, różnicę oraz najmniejszy dodatni wyraz ciągu 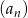 .
.
Jeden z kątów trójkąta jest cztery razy mniejszy od mniejszego z dwóch pozostałych kątów, które różnią się o 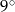 . Oblicz kąty tego trójkąta.
. Oblicz kąty tego trójkąta.
Dany jest stożek o polu powierzchni bocznej równym 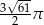 , w którym tangens kąta nachylenia tworzącej do podstawy jest równy
, w którym tangens kąta nachylenia tworzącej do podstawy jest równy  . Oblicz objętość tego stożka.
. Oblicz objętość tego stożka.

