/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (CKE)
poziom podstawowy 4 marca 2022 Czas pracy: 180 minut
Wartość wyrażenia 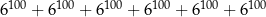 jest równa
jest równa
A) 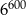 B)
B) 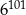 C)
C) 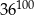 D)
D) 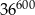
Wartość wyrażenia 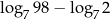 jest równa
jest równa
A) 7 B) 2 C) 1 D) 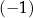
Wszystkich liczb naturalnych trzycyfrowych, w których zapisie dziesiętnym nie występuje cyfra 2, jest
A) 900 B) 729 C) 648 D) 512
Dla każdej liczby rzeczywistej  wartość wyrażenia
wartość wyrażenia 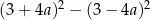 jest równa
jest równa
A) 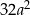 B) 0 C)
B) 0 C) 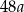 D)
D) 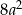
Dane są dwie przecinające się proste. Miary kątów utworzonych przez te proste zapisano za pomocą wyrażeń algebraicznych (zobacz rysunek).

Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Układem równań, w którym zapisano prawidłowe zależności między miarami kątów utworzonych przez te proste, jest układ
A) 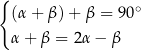 B)
B) 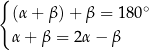 C)
C) 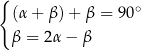
D) 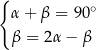 E)
E) 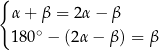 F)
F) 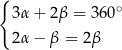
Dany jest wielomian 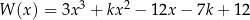 gdzie
gdzie 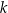 jest pewną liczbą rzeczywistą. Wiadomo, że liczba
jest pewną liczbą rzeczywistą. Wiadomo, że liczba 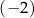 jest pierwiastkiem tego wielomianu. Liczba
jest pierwiastkiem tego wielomianu. Liczba 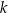 jest równa
jest równa
A) 2 B) 4 C) 6 D) 8
Równanie
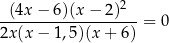
ma w zbiorze liczb rzeczywistych
A) dokładnie jedno rozwiązanie: 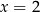 .
.
B) dokładnie dwa rozwiązania: 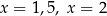 .
.
C) dokładnie trzy rozwiązania: 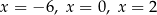 .
.
D) dokładnie cztery rozwiązania: 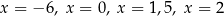 .
.
Spośród rysunków A–D wybierz ten, na którym prawidłowo zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających nierówność
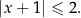

Wykaż, że dla każdej liczby całkowitej nieparzystej  liczba
liczba 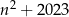 jest podzielna przez 8.
jest podzielna przez 8.
Informacja do zadań 10.1 – 10.3
Dana jest funkcja kwadratowa 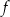 , której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych
, której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych 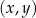 na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 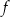 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
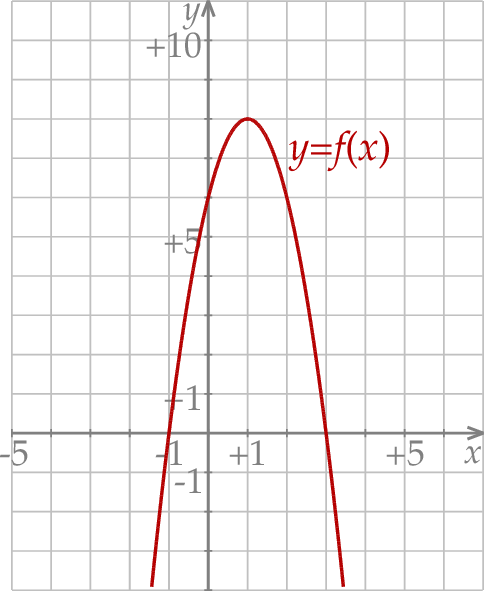
Funkcja 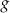 jest określona za pomocą funkcji
jest określona za pomocą funkcji 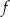 następująco:
następująco: 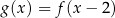 . Wykres funkcji
. Wykres funkcji 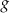 przedstawiono na rysunku
przedstawiono na rysunku
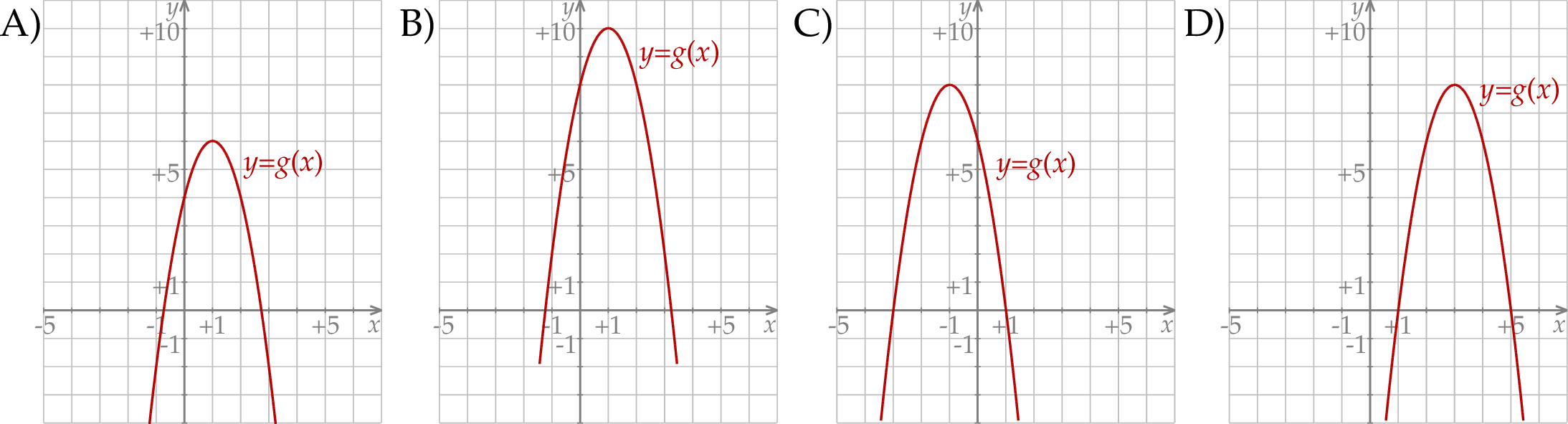
Rozwiąż nierówność 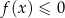 .
.
Wyznacz wzór funkcji kwadratowej 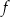 w postaci kanonicznej.
w postaci kanonicznej.
Dana jest funkcja liniowa 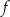 określona wzorem
określona wzorem 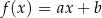 , gdzie
, gdzie  i
i 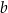 są liczbami rzeczywistymi. Wykres funkcji
są liczbami rzeczywistymi. Wykres funkcji 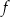 przedstawiono w kartezjańskim układzie współrzędnych
przedstawiono w kartezjańskim układzie współrzędnych 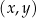 na rysunku poniżej
na rysunku poniżej
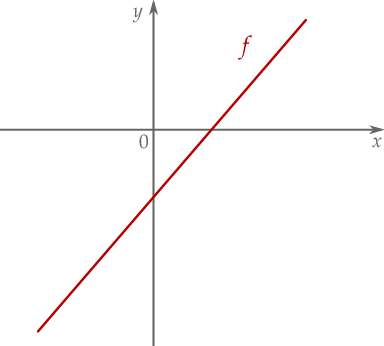
Współczynniki  i
i 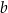 we wzorze funkcji
we wzorze funkcji 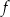 spełniają warunki
spełniają warunki
A) 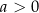 i
i 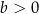 B)
B) 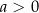 i
i 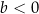 C)
C) 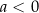 i
i 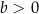 D)
D) 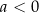 i
i 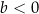
Firma przeprowadziła badania rynkowe dotyczące wpływu zmiany ceny 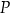 swojego produktu na liczbę
swojego produktu na liczbę 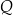 kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 1 jednostkę powoduje spadek liczby kupujących o 3 jednostki. Ponadto przy cenie równej 5 jednostek liczba kupujących jest równa 12 jednostek. Funkcja, która opisuje zależność liczby kupujących ten produkt od jego ceny, ma wzór
kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 1 jednostkę powoduje spadek liczby kupujących o 3 jednostki. Ponadto przy cenie równej 5 jednostek liczba kupujących jest równa 12 jednostek. Funkcja, która opisuje zależność liczby kupujących ten produkt od jego ceny, ma wzór
A) 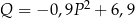 B)
B) 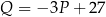
C) 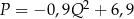 D)
D) 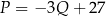
Informacja do zadań 13.1 i 13.2
Czas 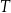 półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa
półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 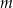 leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
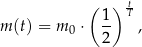
gdzie:
-
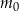 – masa przyjętej dawki leku,
– masa przyjętej dawki leku, -
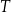 – czas półtrwania leku,
– czas półtrwania leku, -
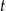 – czas liczony od momentu przyjęcia dawki.
– czas liczony od momentu przyjęcia dawki.
W przypadku przyjęcia kilku(nastu) dawek powyższa zależność pozwala obliczyć, ile leku pozostało w danym momencie w organizmie z każdej poprzednio przyjętej dawki. W ten sposób obliczone masy leku z przyjętych poprzednich dawek sumują się i dają informację o całkowitej aktualnej masie leku w organizmie.
Pacjent otrzymuje co 4 dni o tej samej godzinie dawkę 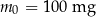 leku L. Czas półtrwania tego leku w organizmie jest równy
leku L. Czas półtrwania tego leku w organizmie jest równy 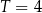 doby.
doby.
Wykres zależności masy 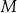 leku L w organizmie tego pacjenta od czasu
leku L w organizmie tego pacjenta od czasu 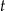 , liczonego od momentu przyjęcia przez pacjenta pierwszej dawki, przedstawiono na rysunku
, liczonego od momentu przyjęcia przez pacjenta pierwszej dawki, przedstawiono na rysunku
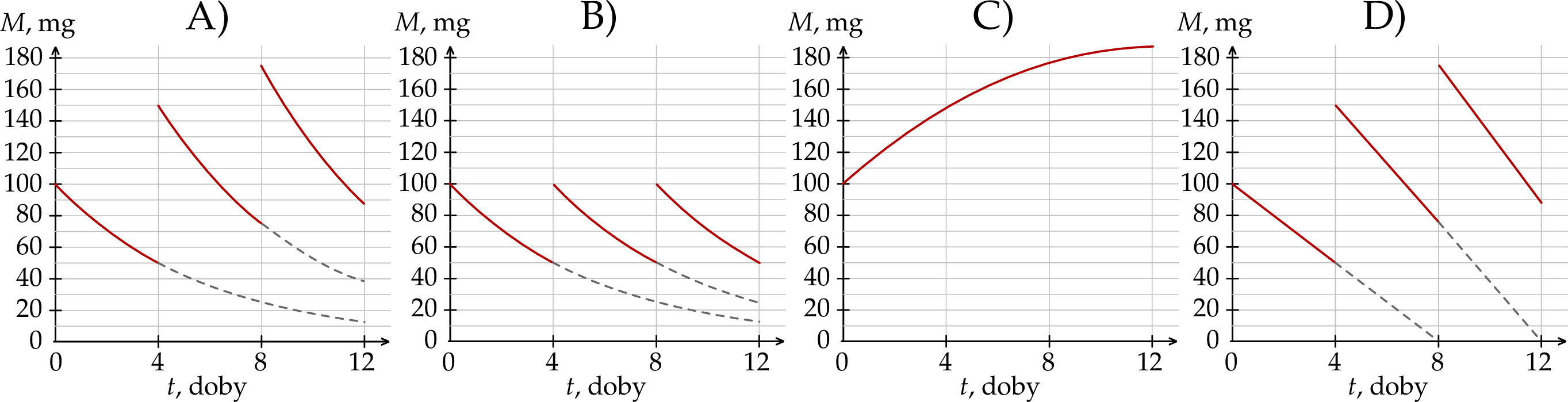
Oblicz masę leku L w organizmie tego pacjenta tuż przed przyjęciem jedenastej dawki tego leku. Wynik podaj w zaokrągleniu do 0,1 mg.
Klient wpłacił do banku 20 000 zł na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości 3% od kwoty bieżącego kapitału znajdującego się na lokacie. Po 2 latach oszczędzania w tym banku kwota na lokacie (bez uwzględniania podatków) jest równa
A) 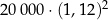 B)
B) 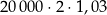 C)
C) 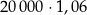 D)
D) 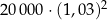
Dany jest ciąg 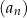 określony wzorem
określony wzorem 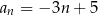 dla każdej liczby naturalnej
dla każdej liczby naturalnej 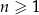 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczby 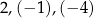 są trzema kolejnymi początkowymi wyrazami ciągu są trzema kolejnymi początkowymi wyrazami ciągu 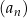 . . | P | F |
Ciąg 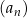 jest ciągiem arytmetycznym o różnicy równej 5. jest ciągiem arytmetycznym o różnicy równej 5. | P | F |
Dany jest trójkąt 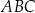 , w którym
, w którym 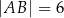 ,
, 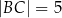 ,
, 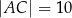 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Cosinus kąta 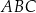 jest równy jest równy 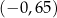 . . | P | F |
Trójkąt 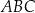 jest rozwartokątny. jest rozwartokątny. | P | F |
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 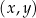 , dany jest okrąg o środku
, dany jest okrąg o środku 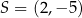 i promieniu
i promieniu 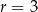 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 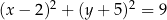 B)
B) 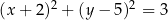
C) 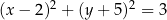 D)
D) 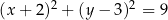
Odcinki 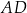 i
i 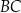 przecinają się w punkcie
przecinają się w punkcie 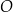 . W trójkątach
. W trójkątach 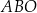 i
i 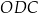 zachodzą związki:
zachodzą związki: 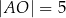 ,
, 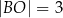 ,
, 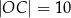 ,
, 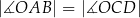 (zobacz rysunek).
(zobacz rysunek).
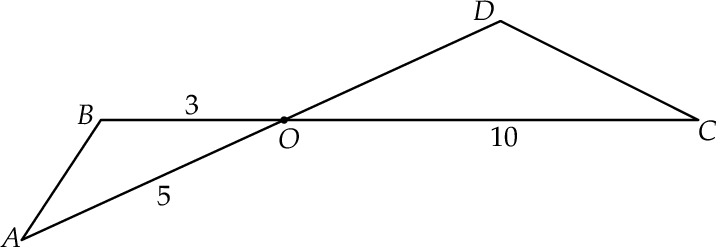
Oblicz długość boku 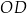 trójkąta
trójkąta 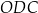 .
.
Informacja do zadań 19.1 i 19.2
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 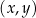 , dana jest prosta
, dana jest prosta 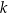 o równaniu
o równaniu 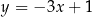 .
.
Jedną z prostych równoległych do prostej 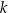 jest prosta o równaniu
jest prosta o równaniu
A) 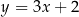 B)
B) 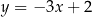 C)
C) 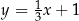 D)
D) 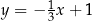
Jedną z prostych prostopadłych do prostej 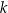 jest prosta o równaniu
jest prosta o równaniu
A) 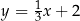 B)
B) 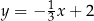 C)
C) 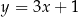 D)
D) 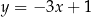
W kartezjańskim układzie współrzędnych 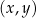 dany jest kwadrat
dany jest kwadrat 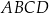 . Wierzchołki
. Wierzchołki 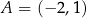 i
i 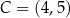 są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu
są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu 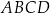 jest równa
jest równa
A) 10 B) 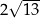 C)
C) 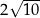 D) 8
D) 8
Odcinek 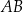 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 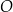 i promieniu
i promieniu 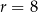 (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 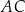 ma długość
ma długość 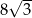 .
.

Miara kąta 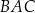 jest równa
jest równa
A) 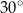 B)
B) 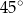 C)
C) 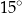 D)
D) 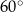
Kąt  jest ostry oraz
jest ostry oraz 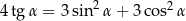 . Tangens kąta
. Tangens kąta  jest równy
jest równy
A) 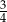 B)
B) 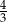 C)
C) 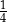 D) 4
D) 4
Dane są dwa trójkąty podobne 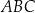 i
i 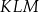 o polach równych – odpowiednio –
o polach równych – odpowiednio – 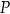 oraz
oraz 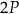 . Obwód trójkąta
. Obwód trójkąta 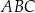 jest równy
jest równy  .
.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1, 2 albo 3.
Obwód trójkąta 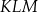 jest równy
jest równy
A) 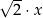 , , | B) 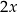 , , |
| ponieważ stosunek obwodów trójkątów podobnych jest równy | |
| 1) | kwadratowi stosunku pól tych trójkątów. |
| 2) | pierwiastkowi kwadratowemu ze stosunku pól tych trójkątów. |
| 3) | stosunkowi pól tych trójkątów. |
Punkty 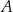 oraz
oraz 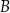 leżą na okręgu o środku
leżą na okręgu o środku 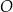 . Proste
. Proste 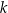 i
i 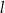 są styczne do tego okręgu w punktach – odpowiednio –
są styczne do tego okręgu w punktach – odpowiednio – 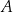 i
i 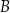 . Te proste przecinają się w punkcie
. Te proste przecinają się w punkcie 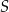 i tworzą kąt o mierze
i tworzą kąt o mierze 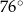 (zobacz rysunek).
(zobacz rysunek).

Miara kąta 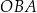 jest równa
jest równa
A) 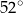 B)
B) 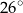 C)
C) 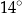 D)
D) 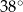
Powierzchnię boczną graniastosłupa prawidłowego czworokątnego rozcięto wzdłuż krawędzi bocznej graniastosłupa i rozłożono na płaszczyźnie. Otrzymano w ten sposób prostokąt 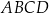 , w którym bok
, w którym bok 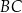 odpowiada krawędzi rozcięcia (wysokości graniastosłupa). Przekątna
odpowiada krawędzi rozcięcia (wysokości graniastosłupa). Przekątna 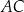 tego prostokąta ma długość 16 i tworzy z bokiem
tego prostokąta ma długość 16 i tworzy z bokiem 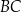 kąt o mierze
kąt o mierze 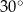 (zobacz rysunek).
(zobacz rysunek).
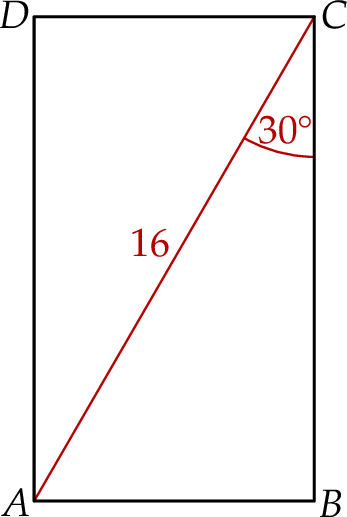
Długość krawędzi podstawy tego graniastosłupa jest równa.
A) 8 B) 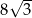 C)
C) 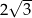 D) 2
D) 2
Dany jest ostrosłup prawidłowy trójkątny 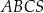 o podstawie
o podstawie 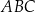 . Punkty
. Punkty 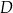 ,
, 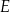 i
i 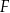 są środkami – odpowiednio – krawędzi bocznych
są środkami – odpowiednio – krawędzi bocznych 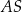 ,
, 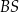 i
i 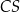 (zobacz rysunek).
(zobacz rysunek).
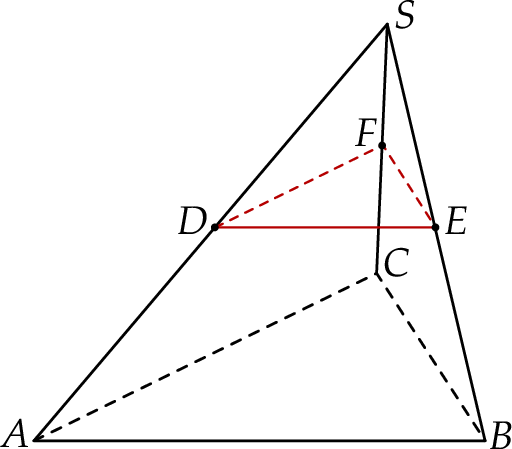
Stosunek objętości ostrosłupa 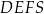 do objętości ostrosłupa
do objętości ostrosłupa 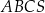 jest równy
jest równy
A) 3 : 4 B) 1 : 4 C) 1 : 8 D) 3 : 8
Dany jest graniastosłup prawidłowy trójkątny 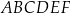 . Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt
. Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt  pomiędzy ścianą boczną
pomiędzy ścianą boczną 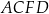 i przekątną
i przekątną 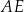 ściany bocznej
ściany bocznej 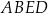 tego graniastosłupa?
tego graniastosłupa?
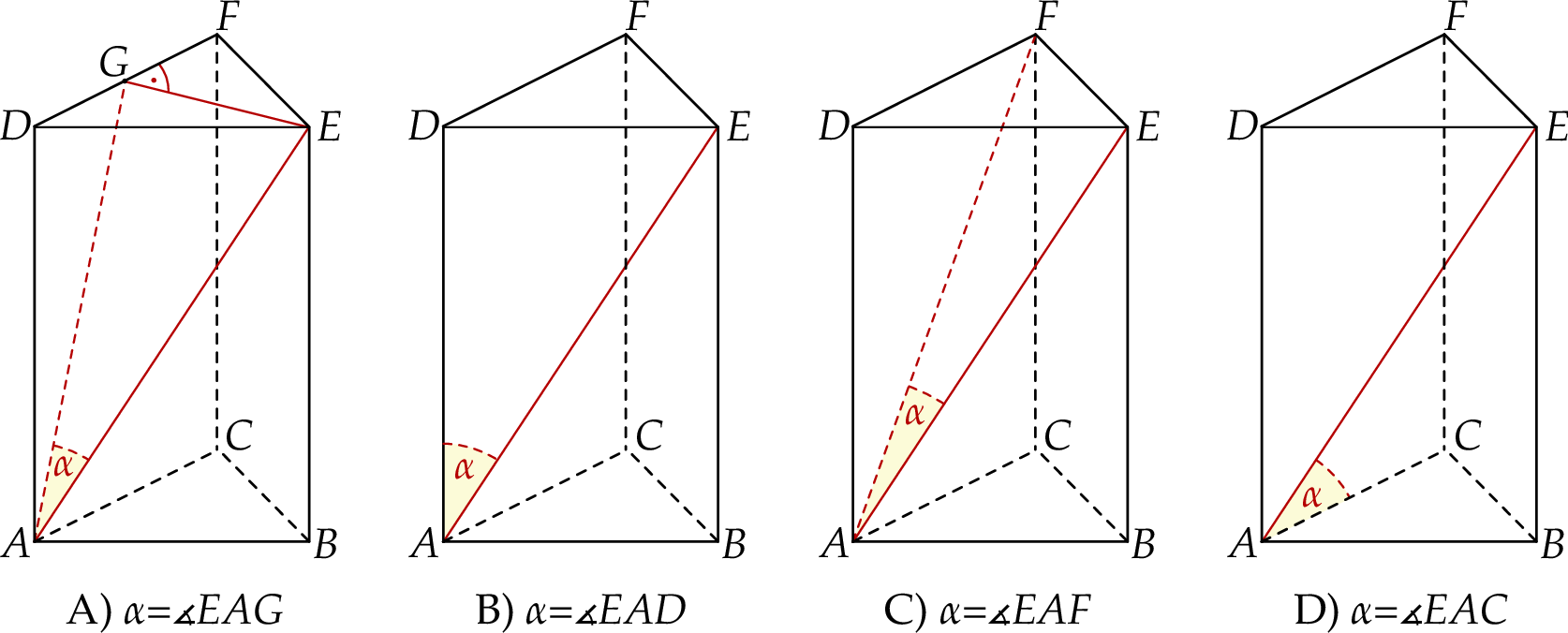
W pojemniku znajdują się losy loterii fantowej ponumerowane kolejnymi liczbami naturalnymi od 1000 do 9999. Każdy los, którego numer jest liczbą o sumie cyfr równej 3, jest wygrywający. Uczestnicy loterii losują z pojemnika po jednym losie. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że pierwszy los wyciągnięty z pojemnika był wygrywający.
Rozważamy wszystkie równoległoboki o obwodzie równym 200 i kącie ostrym o mierze 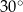 .
.
-
Podaj wzór i dziedzinę funkcji opisującej zależność pola takiego równoległoboku od długości
 boku równoległoboku.
boku równoległoboku. -
Oblicz wymiary tego z rozważanych równoległoboków, który ma największe pole, i oblicz to największe pole.
Informacja do zadań 30.1 i 30.2
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
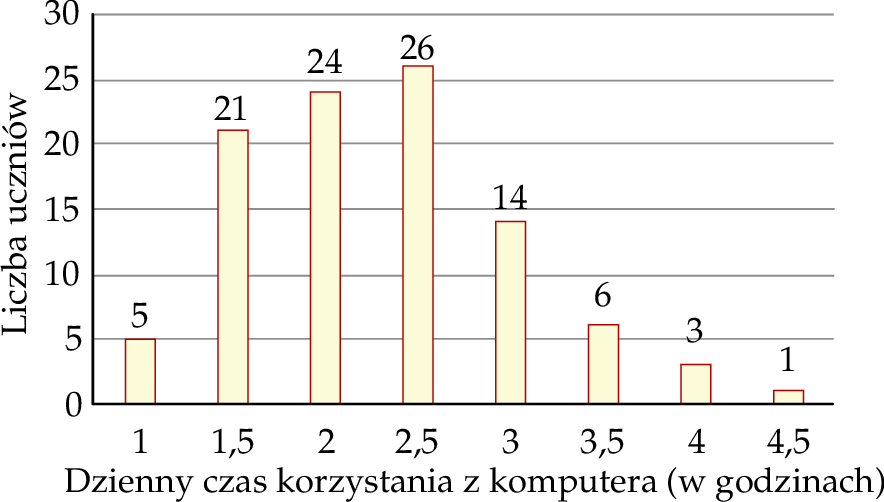
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Mediana dziennego czasu korzystania przez ucznia z komputera jest równa 2,25 godziny. | P | F |
| Połowa z tej grupy uczniów korzysta dziennie z komputera przez mniej niż 2,5 godziny. | P | F |
Dominanta dziennego czasu korzystania przez ucznia z komputera jest równa
A) 2,25 godziny B) 2,50 godziny C) 2,75 godziny D) 1,50 godziny

