/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 10 marca 2018 Czas pracy: 170 minut
Zadania zamknięte
Liczba 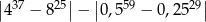 jest równa
jest równa
A) 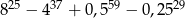
B) 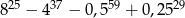
C) 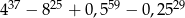
D) 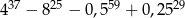
Dane są dwa koła. Promień pierwszego koła jest większy od promienia drugiego koła o 20%. Wynika stąd, że pole pierwszego koła jest większe od pola drugiego koła
A) o mniej niż 50%, ale więcej niż 40%.
B) o mniej niż 60% , ale więcej niż 50%.
C) dokładnie o 60%.
D) o więcej niż 60%.
Różnica 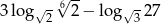 jest równa
jest równa
A) 7 B) 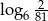 C)
C) 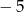 D)
D) 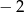
Zbiorem rozwiązań nierówności 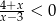 jest
jest
A) 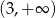 B)
B) 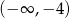 C)
C) 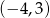 D)
D) 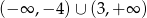
Dla każdej liczby dodatniej 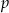 wyrażenie
wyrażenie 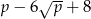 jest równe
jest równe
A) 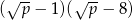
B) 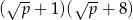
C) 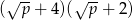
D) 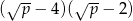
Najmniejszą wartością funkcji kwadratowej 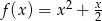 jest
jest
A) 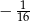 B)
B) 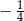 C)
C) 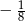 D)
D) 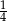
Wskaż rysunek, na którym przedstawiony jest zbiór wszystkich rozwiązań nierówności 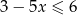 .
.
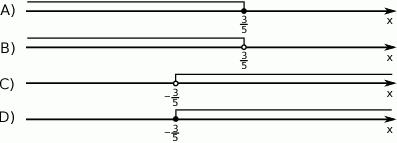
Rozwiązaniem układu równań 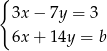 z niewiadomymi
z niewiadomymi  i
i 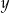 jest para liczb, których suma jest równa 0. Wynika stąd, że
jest para liczb, których suma jest równa 0. Wynika stąd, że
A) 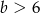 B)
B) 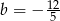 C)
C) 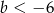 D)
D) 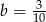
Liczba 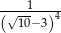 jest równa
jest równa
A) 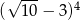 B)
B) 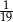 C)
C) 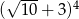 D)
D) 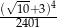
Równanie 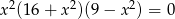 ma dokładnie
ma dokładnie
A) pięć rozwiązań: 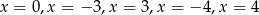
B) trzy rozwiązania: 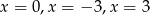
C) dwa rozwiązania: 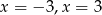
D) jedno rozwiązanie: 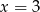
Dany jest ciąg arytmetyczny 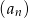 , określony dla
, określony dla 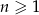 , o którym wiemy, że:
, o którym wiemy, że: 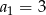 i
i 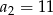 . Wtedy
. Wtedy 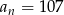 dla
dla
A) 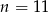 B)
B) 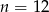 C)
C) 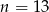 D)
D) 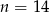
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 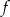 określonej wzorem
określonej wzorem 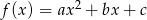 .
.
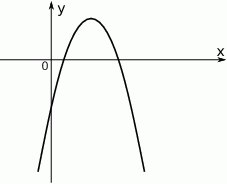
Współczynniki 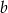 i
i  spełniają warunki:
spełniają warunki:
A) 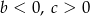 B)
B) 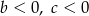 C)
C) 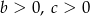 D)
D) 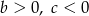
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej 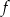 określonej wzorem
określonej wzorem 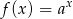 . Wartość funkcji dla
. Wartość funkcji dla 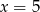 jest cztery razy większa, niż wartość dla
jest cztery razy większa, niż wartość dla 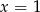 .
.
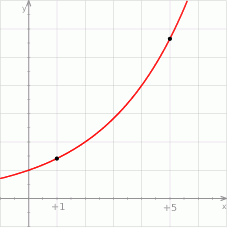
Podstawa  potęgi jest równa
potęgi jest równa
A) 2 B) 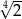 C)
C) 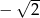 D)
D) 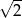
Kąt  jest ostry i
jest ostry i 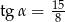 . Wówczas
. Wówczas 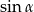 jest równy
jest równy
A) 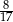 B)
B) 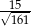 C)
C) 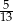 D)
D) 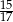
Na okręgu o środku w punkcie 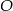 leży punkt
leży punkt 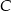 (zobacz rysunek). Odcinek
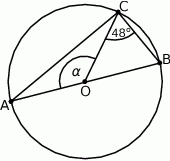
(zobacz rysunek). Odcinek 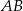 jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy
jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy  ma miarę
ma miarę
A) 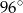 B)
B) 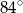 C)
C) 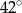 D)
D) 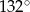
Dany jest ciąg geometryczny
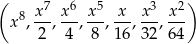
o wyrazach dodatnich. Wtedy
A) 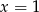 B)
B) 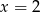 C)
C) 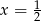 D)
D) 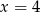
Każda z dwudziestu ścian dwudziestościanu foremnego jest trójkątem równobocznym. Liczba wszystkich krawędzi dwudziestościanu foremnego jest równa
A) 60 B) 30 C) 15 D) 20
Dany jest sześciokąt foremny, którego pole jest równe 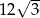 . Bok tego sześciokąta ma długość
. Bok tego sześciokąta ma długość
A) 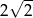 B) 8 C) 4 D)
B) 8 C) 4 D) 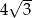
Punkt 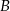 jest rzutem prostopadłym punktu
jest rzutem prostopadłym punktu 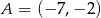 na prostą o równaniu
na prostą o równaniu 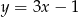 . Wskaż równanie prostej
. Wskaż równanie prostej 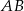 .
.
A) 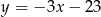 B)
B) 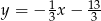 C)
C) 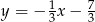 D)
D) 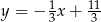
Trójkąt 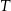 jest podobny do trójkąta
jest podobny do trójkąta 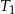 w skali
w skali 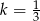 , a trójkąt
, a trójkąt 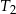 jest podobny do trójkąta
jest podobny do trójkąta 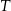 w skali
w skali 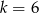 . Pole trójkąta
. Pole trójkąta 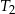 jest równe 32. Trójkąt
jest równe 32. Trójkąt 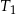 ma pole równe
ma pole równe
A) 128 B) 8 C) 16 D) 24
Prosta 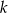 oraz prosta o równaniu
oraz prosta o równaniu 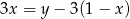 są prostopadłe oraz przecinają się w punkcie
są prostopadłe oraz przecinają się w punkcie 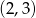 . Prosta
. Prosta 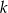 ma równanie
ma równanie
A) 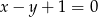 B)
B) 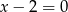 C)
C) 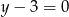 D)
D) 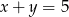
Jedno z ramion kąta  (rysunek) leży na osi odciętych, a drugie przechodzi przez punkt
(rysunek) leży na osi odciętych, a drugie przechodzi przez punkt 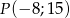 .
.
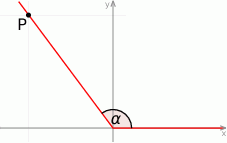
Zatem 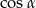 jest równy
jest równy
A) 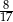 B)
B) 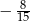 C)
C) 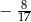 D)
D) 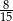
Ile jest wszystkich czterocyfrowych liczb naturalnych podzielnych przez 7?
A) 1285 B) 1428 C) 1284 D) 1286
Dany jest stożek o wysokości 5 i średnicy podstawy 6. Objętość tego stożka jest równa
A) 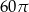 B)
B) 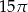 C)
C) 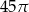 D)
D) 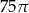
Rzucamy sześć razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sześciu różnych liczb oczek, jest równe
A) 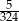 B)
B) 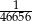 C)
C)  D)
D) 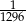
Zadania otwarte
Wykaż, że 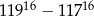 jest liczbą podzielną przez 59.
jest liczbą podzielną przez 59.
Rozwiąż nierówność 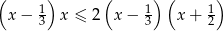 .
.
Dwusieczna kąta ostrego 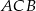 przecina przyprostokątną
przecina przyprostokątną 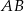 trójkąta prostokątnego
trójkąta prostokątnego 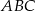 w punkcie
w punkcie 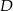 .
.
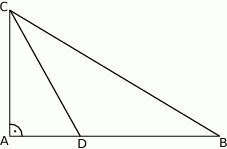
Udowodnij, że jeżeli 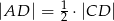 , to
, to 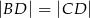 .
.
Wykaż, ze dla dowolnych liczb rzeczywistych 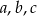 prawdziwa jest nierówność
prawdziwa jest nierówność
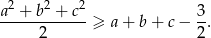
Oblicz
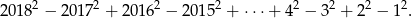
Ze zbioru liczb trzycyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że iloczyn cyfr wylosowanej liczby jest liczbą parzystą?
Funkcja kwadratowa 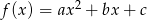 ma dwa miejsca zerowe
ma dwa miejsca zerowe 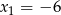 i
i 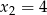 . Wykres funkcji
. Wykres funkcji 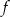 przechodzi przez punkt
przechodzi przez punkt 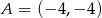 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 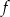 .
.
Dwa boki trójkąta prostokątnego 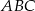 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 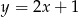 oraz
oraz 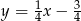 . Wyznacz współrzędne wierzchołków trójkąta
. Wyznacz współrzędne wierzchołków trójkąta 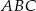 jeżeli wiadomo, że jego trzeci bok jest zawarty w prostej przechodzącej przez punkt
jeżeli wiadomo, że jego trzeci bok jest zawarty w prostej przechodzącej przez punkt 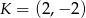 . Rozważ wszystkie możliwości.
. Rozważ wszystkie możliwości.
Dany jest graniastosłup prawidłowy trójkątny 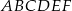 o podstawach
o podstawach 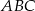 i
i 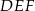 i krawędziach bocznych
i krawędziach bocznych 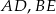 i
i 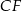 (zobacz rysunek). Krawędzie boczne graniastosłupa mają długość 8, a tangens kąta między wysokością trójkąta
(zobacz rysunek). Krawędzie boczne graniastosłupa mają długość 8, a tangens kąta między wysokością trójkąta 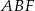 poprowadzoną z wierzchołka
poprowadzoną z wierzchołka 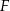 i płaszczyzną podstawy
i płaszczyzną podstawy 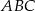 tego graniastosłupa jest równy
tego graniastosłupa jest równy 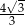 . Oblicz pole trójkąta
. Oblicz pole trójkąta 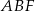 .
.