/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom podstawowy grupa I 31 maja 2011 Czas pracy: 170 minut
Zadania zamknięte
Równanie 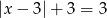 ma:
ma:
A) jedno rozwiązanie
B) dwa rozwiązania
C) nieskończenie wiele rozwiązań
D) zero rozwiązań
Wyrażenie 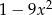 po rozłożeniu na czynniki liniowe ma postać:
po rozłożeniu na czynniki liniowe ma postać:
A) 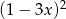 B)
B) 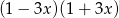 C)
C) 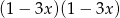 D)
D) 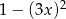
Dla której z liczb wyrażenie 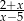 nie ma sensu liczbowego?
nie ma sensu liczbowego?
A) -2 B) -5 C) 0 D) 5
Wyznaczając 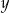 z równania
z równania 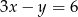 otrzymujemy:
otrzymujemy:
A) 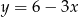 B)
B) 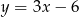 C)
C) 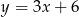 D)
D) 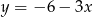
Która z poniższych liczb jest równa ułamkowi: 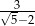 ?
?
A) 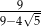 B)
B) 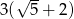 C)
C) 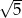 D) 9
D) 9
Do naczynia o pojemności 2,5 l i wlano 0,75 l wody. Jaki procent tego naczynia stanowi objętość wody?
A) 3% B) 60% C) 3,(3)% D) 30%
Obwód prostokąta jest równy 32 cm, a jeden z jego boków jest 3 razy dłuższy od drugiego boku. Pole tego prostokąta jest równe:
A) 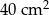 B)
B) 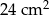 C)
C) 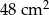 D)
D) 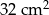
Jeżeli 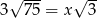 to liczba
to liczba  jest równa
jest równa
A) 25 B) 15 C) 5 D) 75
Liczba 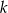 jest średnią arytmetyczną liczb
jest średnią arytmetyczną liczb 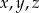 . Wynika stąd, że
. Wynika stąd, że
A) 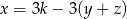 B)
B) 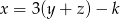 C)
C) 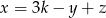 D)
D) 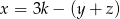
Odcinek podzielono na dwie części w stosunku 1:3. Ile procent całego odcinka stanowi większa jego część?
A) 75% B) 25% C) 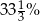 D)
D) 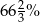
Suma kwadratów liczb 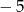 i
i 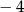 jest równa:
jest równa:
A) 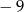 B) 81 C) 41 D)
B) 81 C) 41 D) 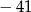
Długościami boków trójkąta mogą być odcinki:
A) 5 cm, 8 cm, 2 cm B) 9 cm, 4 cm, 4 cm C) 3 cm, 2 cm, 1 cm D) 7 cm, 9 cm, 10 cm
W kwadrat wpisano okrąg o promieniu 6 cm. Obwód tego kwadratu jest równy:
A) 12 cm B) 24 cm C) 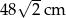 D) 48 cm
D) 48 cm
Miara kąta wewnętrznego ośmiokąta foremnego jest równa:
A) 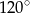 B)
B) 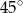 C)
C) 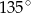 D)
D) 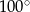
Rozwiązaniem równania 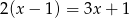 jest liczba:
jest liczba:
A) -3 B) -2 C) 1 D) 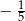
Wyrażenie 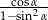 można zapisać w postaci:
można zapisać w postaci:
A) 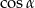 B)
B) 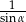 C)
C) 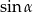 D)
D) 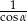
Długość boku trójkąta równobocznego o wysokości 6 cm jest równa:
A) 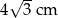 B) 12 cm C)
B) 12 cm C) 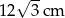 D)
D) 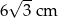
Wartość wyrażenia 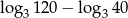 jest równa:
jest równa:
A) 1 B) 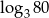 C) 0 D)
C) 0 D) 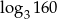
Dla 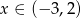 wyrażenie
wyrażenie 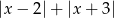 jest równe:
jest równe:
A) 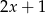 B) -5 C) 1 D) 5
B) -5 C) 1 D) 5
Wyrażenie 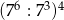 jest równe
jest równe
A) 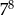 B)
B) 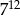 C)
C) 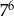 D)
D) 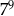
Prosta prostopadła do prostej 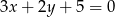 ma równanie:
ma równanie:
A) 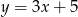 B)
B) 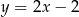 C)
C) 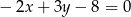 D)
D) 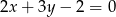
Prosta równoległa do prostej 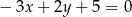 ma równanie:
ma równanie:
A) 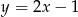 B)
B) 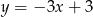 C)
C) 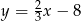 D)
D) 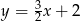
Punkt 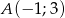 należy do wykresu funkcji:
należy do wykresu funkcji:
A) 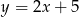 B)
B) 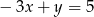 C)
C) 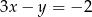 D)
D) 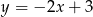
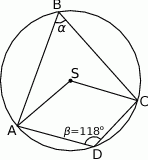
Jaką miarę ma kąt  ?
?
A) 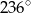 B)
B) 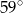 C)
C) 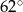 D)
D) 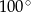
Znajdź skalę podobieństwa trójkąta  do trójkąta
do trójkąta  :
:
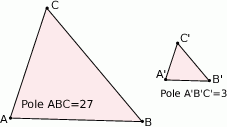
A) 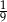 B)
B) 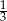 C) 3 D) 9
C) 3 D) 9
Zadania otwarte
Znajdź ułamek o mianowniku 4 leżący na osi liczbowej między 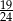 a
a  .
.
Znajdź wszystkie liczby całkowite spełniające nierówność 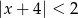 .
.
Udowodnij, że w trójkącie prostokątnym dwusieczna kąta prostego dzieli na połowy kąt zawarty między środkową, a wysokością opuszczoną z wierzchołka kąta prostego.
Wykaż, że liczba 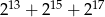 jest podzielna przez 21.
jest podzielna przez 21.
Znaleźć kąt ostry rombu, jeżeli wiadomo, że jego pole jest równe 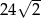 , a promień okręgu w niego wpisanego równy
, a promień okręgu w niego wpisanego równy 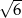 .
.
Wyznacz skalę mapy, na której jezioro o rzeczywistej powierzchni 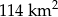 , zajmuje obszar
, zajmuje obszar 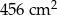 .
.
W dwóch sadach rosło razem 8400 drzewek. W ciągu roku zwiększono liczbę drzewek w każdym sadzie. W pierwszym o 20%, a w drugim o 50%. Okazało się wtedy, że liczba drzewek w pierwszym sadzie jest 2 razy większa niż w drugim. Ile drzew było początkowo w każdym sadzie?
Dana jest funkcja 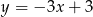 . Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt
. Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt 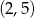 . Wykonaj rysunek do zadania.
. Wykonaj rysunek do zadania.
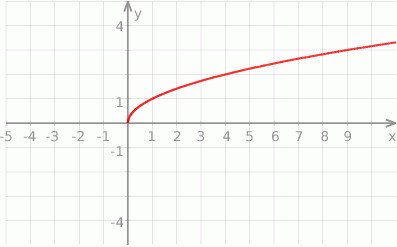
Korzystając z wykresu 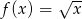 , naszkicuj wykres funkcji
, naszkicuj wykres funkcji 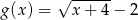 , a następnie odczytaj z wykresu: dziedzinę, zbiór wartości, oraz przedziały w których funkcja
, a następnie odczytaj z wykresu: dziedzinę, zbiór wartości, oraz przedziały w których funkcja 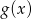 przyjmuje wartości dodatnie.
przyjmuje wartości dodatnie.