/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 26 marca 2011
Zadania zamknięte
Liczba 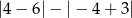 jest równa
jest równa
A) -3 B) -5 C) 3 D) 1
7,5% liczby  jest równe 9. Wtedy
jest równe 9. Wtedy
A) 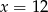 B)
B) 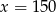 C)
C) 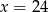 D)
D) 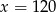
Liczbą odwrotną do 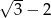 jest
jest
A) 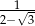 B)
B) 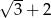 C)
C) 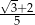 D)
D) 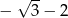
Dana jest liczba 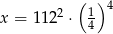 . Wtedy
. Wtedy
A) 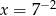 B)
B) 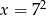 C)
C) 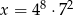 D)
D) 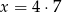
Wyrażenie 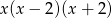 jest równe
jest równe
A) 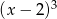 B)
B) 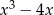 C)
C) 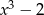 D)
D) 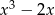
Wartość wyrażenia 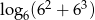 wynosi
wynosi
A) 5 B) 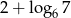 C) 6 D)
C) 6 D) 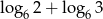
Pole działki budowlanej jest równe 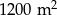 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 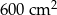 B)
B) 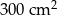 C)
C) 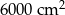 D)
D) 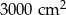
W ciągu geometrycznym 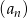 dane są
dane są 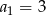 i
i 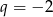 . Suma ośmiu początkowych wyrazów tego ciągu jest równa
. Suma ośmiu początkowych wyrazów tego ciągu jest równa
A) 255 B) -255 C) 257 D) -257
Na rysunku przedstawiony jest wykres funkcji liniowej 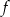 .
.
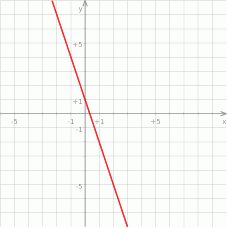
Funkcja 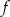 jest określona wzorem
jest określona wzorem
A) 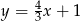 B)
B) 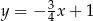 C)
C) 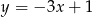 D)
D) 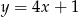
Liczby 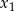 i
i 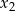 są pierwiastkami równania
są pierwiastkami równania 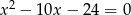 i
i 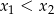 . Oblicz
. Oblicz 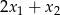 .
.
A) -22 B) -17 C) 8 D) 13
W ciągu arytmetycznym 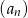 dane są:
dane są: 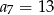 i
i 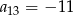 . Wtedy wyraz
. Wtedy wyraz 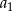 jest równy
jest równy
A) -4 B) 24 C) 37 D) -24
Osią symetrii paraboli będącej wykresem funkcji 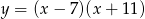 jest prosta o równaniu
jest prosta o równaniu
A) 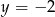 B)
B) 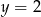 C)
C) 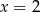 D)
D) 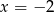
Rozwiązaniem równania 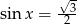 dla
dla 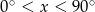 jest
jest
A) 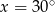 B)
B) 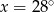 C)
C) 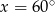 D)
D) 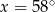
Liczby 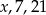 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba  jest równa
jest równa
A) 1 B)  C)
C) 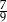 D)
D) 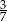
Boisko piłkarskie ma kształt prostokąta o bokach długości 71 m i 106 m. W przeciwległych narożnikach boiska wbito słupki. Odległość między tymi słupkami jest
A) równa 105 m
B) większa niż 125 m
C) większa niż 120 m i mniejsza niż 125 m
D) większa niż 105 m i mniejsza niż 120 m
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 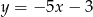 jest równy
jest równy
A) 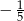 B) 5 C)
B) 5 C) 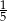 D) -5
D) -5
Okrąg wpisany w trójkąt równoboczny ma promień równy 6. Wysokość tego trójkąta jest równa
A) 18 B) 20 C) 36 D) 24
Pole trójkąta prostokątnego równoramiennego wynosi 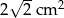 . Zatem przyprostokątna ma długość:
. Zatem przyprostokątna ma długość:
A) 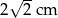 B)
B) 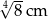 C)
C) 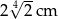 D)
D) 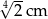
Promień okręgu o równaniu 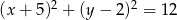 jest równy
jest równy
A) 12 B) 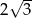 C)
C) 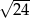 D) 144
D) 144
O zdarzeniach losowych 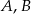 wiadomo, że:
wiadomo, że: 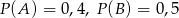 i
i 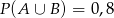 . Prawdopodobieństwo iloczynu zdarzeń
. Prawdopodobieństwo iloczynu zdarzeń 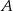 i
i 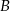 spełnia warunek
spełnia warunek
A) 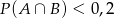 B)
B) 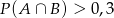 C)
C) 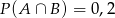 D)
D) 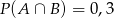
Ostrosłup ma 19 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 19 B) 18 C) 36 D) 38
W karcie dań są 4 zupy i 6 drugich dań. Na ile sposobów można zamówić obiad składający się z jednej zupy i jednego drugiego dania?
A) 24 B) 10 C) 16 D) 30
Zadania otwarte
Rozwiąż nierówność: 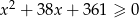 .
.
Rozwiąż równanie 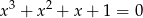 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 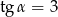 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 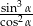 .
.
Za 4 lata Ula będzie miała dwa razy więcej lat niż miała 2 lata temu. Ile lat ma Ula?
Wykaż, że różnica kwadratów dwóch kolejnych liczb nieparzystych jest liczbą podzielną przez 8.
W trapezie prostokątnym krótsza przekątna ma długość ramienia trapezu i dzieli go na dwa trójkąty prostokątne. Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.
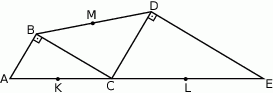
Trójkąty 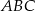 i
i 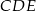 są prostokątne oraz
są prostokątne oraz 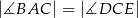 . Punkty
. Punkty 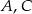 i
i 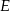 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 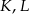 i
i 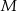 są środkami odcinków
są środkami odcinków 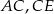 i
i 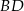 (zobacz rysunek). Wykaż, że kąt
(zobacz rysunek). Wykaż, że kąt 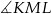 jest prosty.
jest prosty.
Dany jest graniastosłup prawidłowy trójkątny 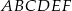 o podstawach
o podstawach 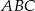 i
i 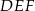 i krawędziach bocznych
i krawędziach bocznych 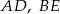 i
i 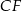 . Oblicz pole trójkąta
. Oblicz pole trójkąta 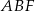 wiedząc, że
wiedząc, że 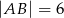 i
i 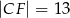 . Narysuj ten graniastosłup i zaznacz na nim trójkąt
. Narysuj ten graniastosłup i zaznacz na nim trójkąt 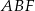 .
.
Oblicz pole czworokąta 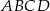 , którego wierzchołki mają współrzędne
, którego wierzchołki mają współrzędne 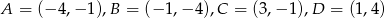 .
.
Kilku znajomych wybrało się na obiad, którego łączny koszt wyniósł 192 zł. Płacąc za obiad postanowili kwotę rachunku podzielić równo pomiędzy wszystkie obecne osoby. Okazało się jednak, że dwie osoby nie wzięły pieniędzy. W tej sytuacji każdy z pozostałych zapłacił o 8 zł więcej, niż powinien. Oblicz, ile osób uczestniczyło w obiedzie.

